12.2.2 单项式与多项式相乘 课件(17张PPT)
文档属性
| 名称 | 12.2.2 单项式与多项式相乘 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 08:50:48 | ||
图片预览






文档简介
(共17张PPT)
12.2.2 单项式与多项式相乘
华师大版 八年级上册
教学目标
1.能说出单项式与多项式相乘的法则,并且知道单项式乘以多项式的结果仍然是多项式.
2.会进行单项式乘以多项式的计算以及含有单项式乘以多项式的混合运算.
3.通过例题教学,培养学生灵活运用所学知识分析问题、解决问题的能力.
【教学重点】掌握单项式乘以多项式的法则.
【教学难点】熟练地运用法则,准确地进行计算.
新知导入
2.完成下列各题.
(1)2x2·(-4xy)=( );
(2)(-2x2)·(-3xy)=( );
(3)(-ab)·(ab2)=( ).
-8x3y
6x3y
-a2b3
1.单项式乘法法则:
单项式乘单项式:把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,连同它的指数不变,作为积的因式.
注意:系数相乘不要漏掉负号.
新知导入
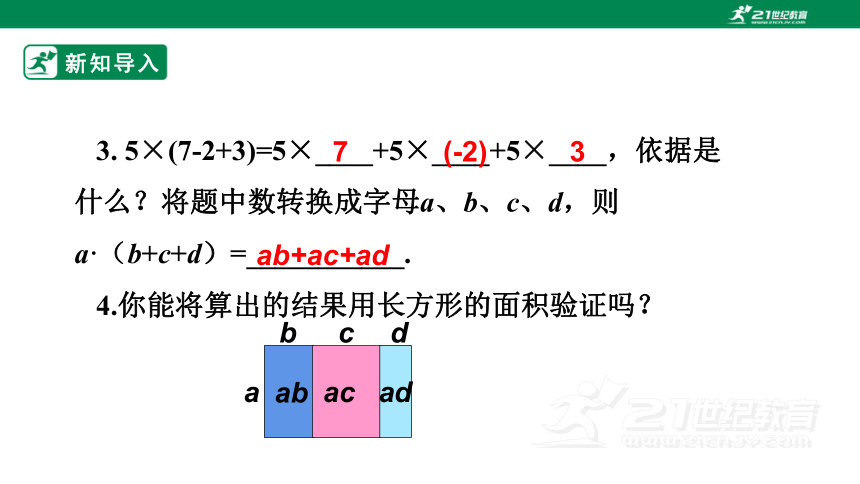
3. 5×(7-2+3)=5×____+5×____+5×____,依据是什么?将题中数转换成字母a、b、c、d,则a·(b+c+d)=___________.
4.你能将算出的结果用长方形的面积验证吗?
7
(-2)
3
a
b
c
d
ab
ac
ad
ab+ac+ad
新知探究
试一试利用乘法分配律计算:2a2·(3a2-5b)
=2a2·3a2
=6a4-10a2b
2a2·(3a2-5b)
2a2·5b
-
例题讲解
例1、 计算: (-2a2)·(3ab2-5ab3).
解 (-2a2)·(3ab2-5ab3)
= (-2a2)·3ab2+(-2a2)·(-5ab3)
=-6a3b2+10a3b3
总结一下,单项式乘以多项式是如何进行计算的?
说一说 运算时要注意哪些问题?
新知讲解
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
① 不能漏乘:即单项式要乘遍多项式的每一项;
② 去括号时注意符号的确定.
巩固练习
(1)3x3y·(2xy2-3xy)
(2)2x·(3x2-xy+y2)
1.计算:
解: 3x3y·(2xy2-3xy)
=3x3y·2xy2-3x3y· 3xy
=6x4y3-9x4y2
解: 2x·(3x2-xy+y2)
=2x·3x2-2x·xy+2x·y2
=6x3-2x2y+2xy2
巩固练习
2.化简:
x(x2-1)+2x2(x+1)-3x(2x-5)
解: x(x2-1)+2x2(x+1)-3x(2x-5)
=x3-x+2x3+2x2-6x2+15x
=3x3-4x2+14x
例题讲解
例2、先化简,再求值:
思路分析:
易错提醒:代值时,遇到分数的乘方,负数的乘方需要添加括号。
例题讲解
例3、解方程:
思路分析:
解题策略:解方程时注意两个变号:移项变号,括号前面是负号要变号。
课堂小结
单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加.
注意:单项式与多项式相乘,在没有合并同类项前,其积仍是多项式,项数与原多项式的项数相同.积的每一项的符号由原多项式各项符号和单项式的符号来决定.
注意运用去括号法则,不要漏乘项.
课堂练习
1、求 的值,其中x=2,y=-1.
当 x=2,y=-1时,
原式的值为 3×23×(-1) +2×22×(-1)2 = -24+8 = -16.
课堂练习
解: yn(yn + 9y-12)-3(3yn+1-4yn)
= y2n+9yn+1-12yn-9yn+1+12yn = y2n
当 y=-3,n=2时,原式=(-3)2×2=(-3)4=81.
2、 先化简,再求值:yn(yn +9y-12)-3(3yn+1-4yn),
其中y=-3,n=2.
课堂练习
3、解方程:
(1)
(2)-5
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2.2 单项式与多项式相乘
华师大版 八年级上册
教学目标
1.能说出单项式与多项式相乘的法则,并且知道单项式乘以多项式的结果仍然是多项式.
2.会进行单项式乘以多项式的计算以及含有单项式乘以多项式的混合运算.
3.通过例题教学,培养学生灵活运用所学知识分析问题、解决问题的能力.
【教学重点】掌握单项式乘以多项式的法则.
【教学难点】熟练地运用法则,准确地进行计算.
新知导入
2.完成下列各题.
(1)2x2·(-4xy)=( );
(2)(-2x2)·(-3xy)=( );
(3)(-ab)·(ab2)=( ).
-8x3y
6x3y
-a2b3
1.单项式乘法法则:
单项式乘单项式:把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,连同它的指数不变,作为积的因式.
注意:系数相乘不要漏掉负号.
新知导入
3. 5×(7-2+3)=5×____+5×____+5×____,依据是什么?将题中数转换成字母a、b、c、d,则a·(b+c+d)=___________.
4.你能将算出的结果用长方形的面积验证吗?
7
(-2)
3
a
b
c
d
ab
ac
ad
ab+ac+ad
新知探究
试一试利用乘法分配律计算:2a2·(3a2-5b)
=2a2·3a2
=6a4-10a2b
2a2·(3a2-5b)
2a2·5b
-
例题讲解
例1、 计算: (-2a2)·(3ab2-5ab3).
解 (-2a2)·(3ab2-5ab3)
= (-2a2)·3ab2+(-2a2)·(-5ab3)
=-6a3b2+10a3b3
总结一下,单项式乘以多项式是如何进行计算的?
说一说 运算时要注意哪些问题?
新知讲解
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
① 不能漏乘:即单项式要乘遍多项式的每一项;
② 去括号时注意符号的确定.
巩固练习
(1)3x3y·(2xy2-3xy)
(2)2x·(3x2-xy+y2)
1.计算:
解: 3x3y·(2xy2-3xy)
=3x3y·2xy2-3x3y· 3xy
=6x4y3-9x4y2
解: 2x·(3x2-xy+y2)
=2x·3x2-2x·xy+2x·y2
=6x3-2x2y+2xy2
巩固练习
2.化简:
x(x2-1)+2x2(x+1)-3x(2x-5)
解: x(x2-1)+2x2(x+1)-3x(2x-5)
=x3-x+2x3+2x2-6x2+15x
=3x3-4x2+14x
例题讲解
例2、先化简,再求值:
思路分析:
易错提醒:代值时,遇到分数的乘方,负数的乘方需要添加括号。
例题讲解
例3、解方程:
思路分析:
解题策略:解方程时注意两个变号:移项变号,括号前面是负号要变号。
课堂小结
单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加.
注意:单项式与多项式相乘,在没有合并同类项前,其积仍是多项式,项数与原多项式的项数相同.积的每一项的符号由原多项式各项符号和单项式的符号来决定.
注意运用去括号法则,不要漏乘项.
课堂练习
1、求 的值,其中x=2,y=-1.
当 x=2,y=-1时,
原式的值为 3×23×(-1) +2×22×(-1)2 = -24+8 = -16.
课堂练习
解: yn(yn + 9y-12)-3(3yn+1-4yn)
= y2n+9yn+1-12yn-9yn+1+12yn = y2n
当 y=-3,n=2时,原式=(-3)2×2=(-3)4=81.
2、 先化简,再求值:yn(yn +9y-12)-3(3yn+1-4yn),
其中y=-3,n=2.
课堂练习
3、解方程:
(1)
(2)-5
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
