人教版九年级上册 23.1 第2课时 旋转作图 课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册 23.1 第2课时 旋转作图 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 332.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 17:44:48 | ||
图片预览


文档简介
(共20张PPT)
23.1 第2课时 旋转作图
第二十三章 旋转
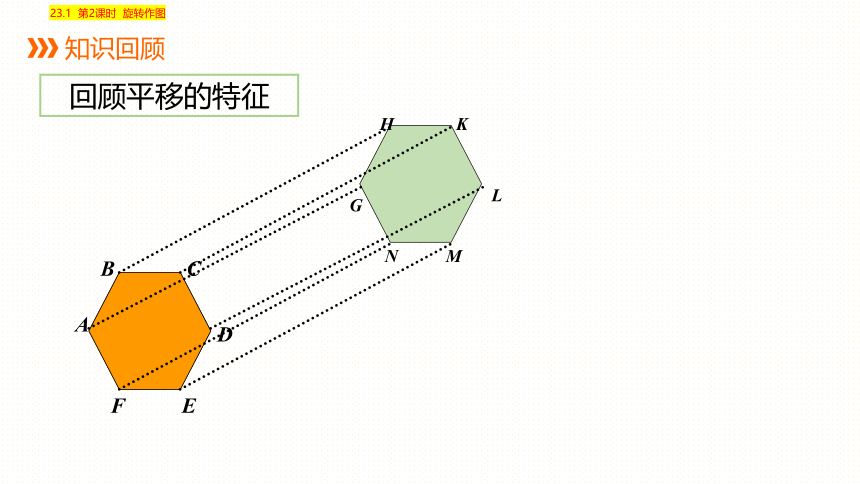
知识回顾
回顾平移的特征
A
B
C
D
E
F
G
H
K
L
M
N
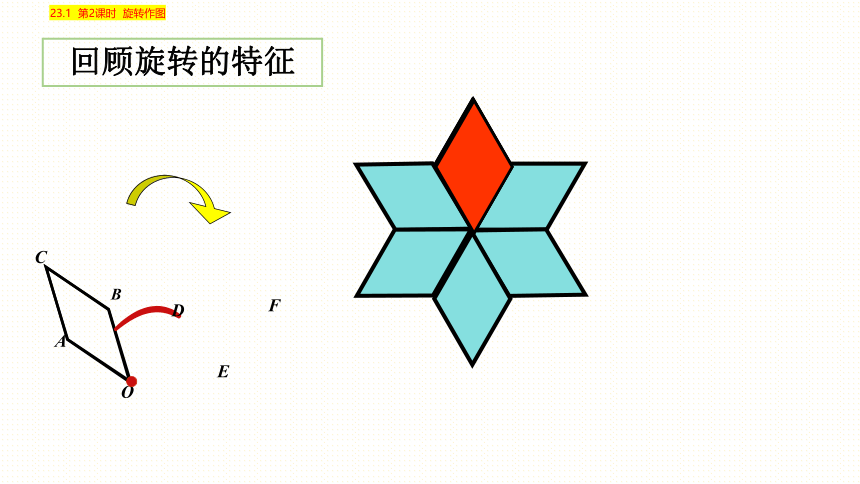
回顾旋转的特征
O
︵
A
B
C
D
E
F
获取新知
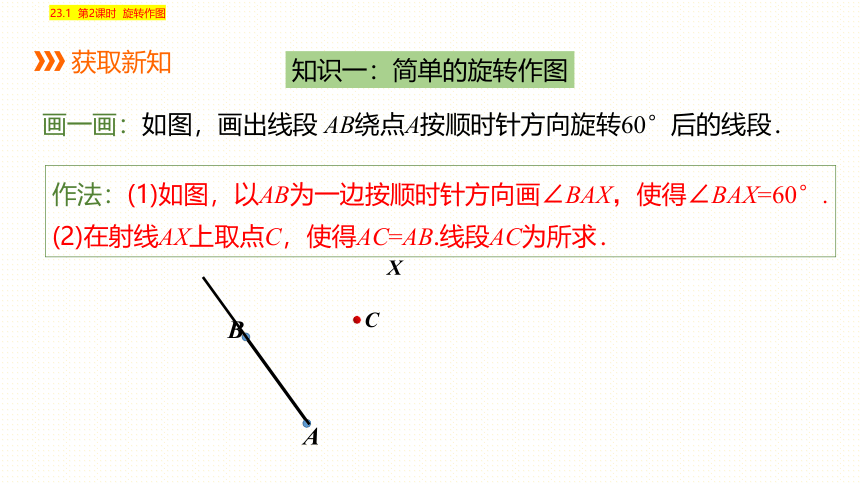
知识一:简单的旋转作图
画一画:如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.线段AC为所求.
A
B
X
C
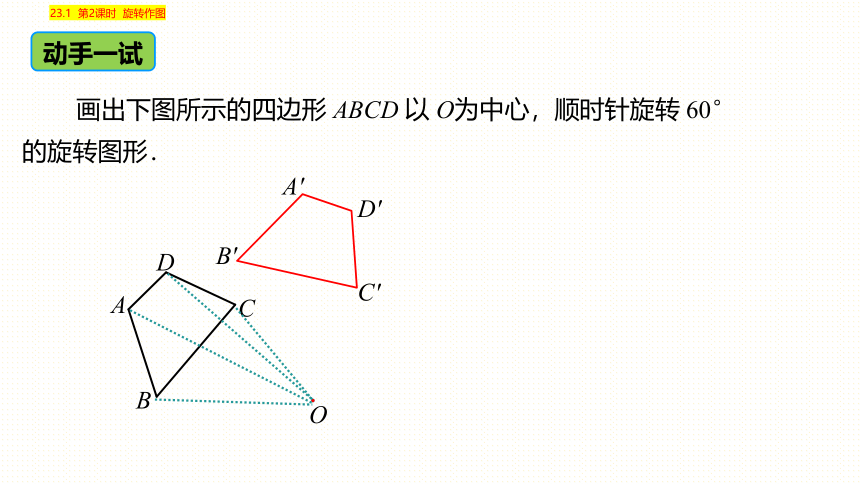
画出下图所示的四边形 ABCD 以 O为中心,顺时针旋转 60°的旋转图形.
A
B
C
D
O
动手一试
B'
A'
C'
D'
(1)定:明确旋转三要素:
旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
(2)找:找出原图的关键点;
(3)作:作出关键点的对应点;
(4)连:连接对应点作出新图形;
(5)写:写出结论.
归纳总结
例题讲解
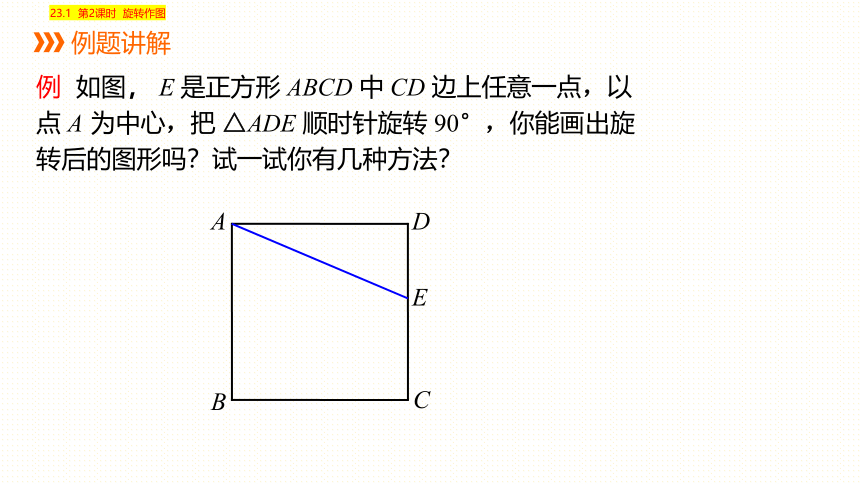
例 如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能画出旋转后的图形吗?试一试你有几种方法?
A
B
C
E
D
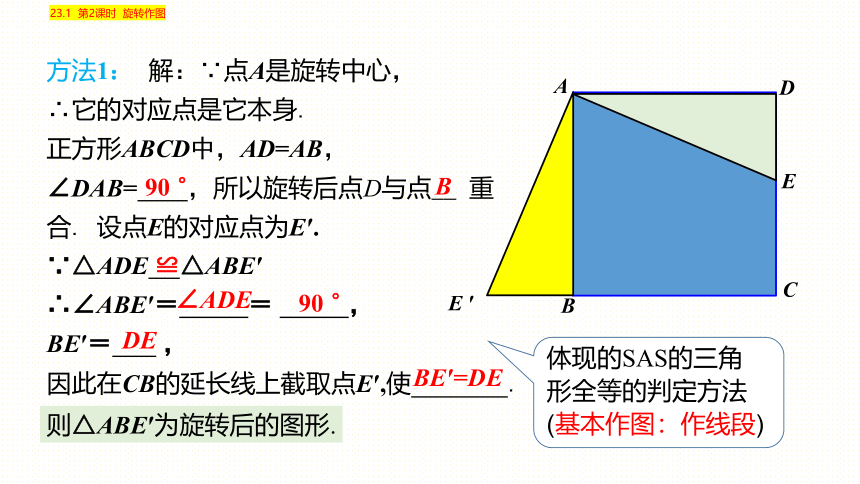
方法1: 解:∵点A是旋转中心,
∴它的对应点是它本身.
正方形ABCD中,AD=AB,
∠DAB= ,所以旋转后点D与点__ 重合. 设点E的对应点为E′.
∵△ADE △ABE′
∴∠ABE′= = ,
BE′= ,
因此在CB的延长线上截取点E′,使 .
A
B
C
D
E
E ′
90 °
≌
∠ADE
90 °
DE
BE′=DE
则△ABE′为旋转后的图形.
B
体现的SAS的三角形全等的判定方法
(基本作图:作线段)
E'
A
B
C
E
D
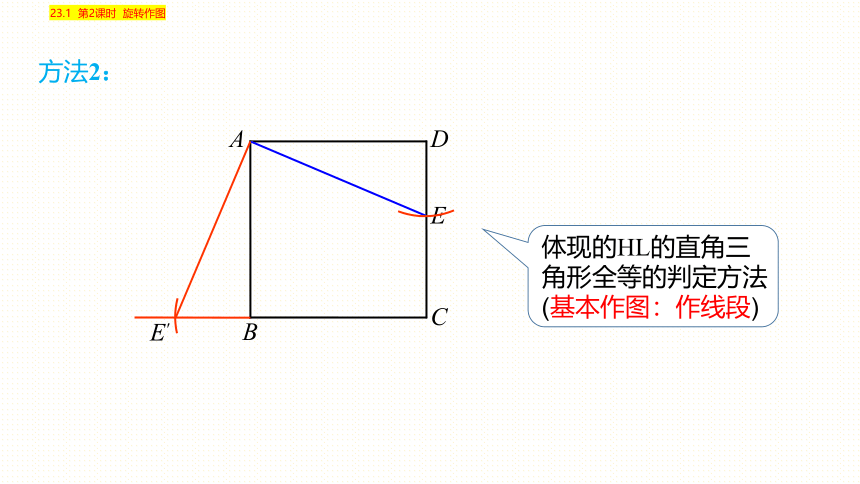
方法2:
体现的HL的直角三角形全等的判定方法
(基本作图:作线段)
方法3:
F
A
B
C
E
D
体现的HL的直角三角形全等的判定方法
(基本作图:作线段)
F
A
B
C
E
D
方法4:
┐
体现的ASA的三角形全等的判定方法
(基本作图:作垂线)
(1)旋转中心不变,改变旋转角(如图).
问题 让我们一起来欣赏一下美丽的图案,体会
一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
O
O
β
α
知识二:旋转设计作图
获取新知
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
(3)美丽的图案是这样形成的.
1.如图,该图形围绕点O按下列角度旋转后,不能与自身重合的是( )
A.72° B.108°
C.144° D.216°
B
随堂演练
2. 下列图案中,可以由一个“基本图案”连续旋转45°得到的是( )
C
3. 如图,△ABC绕点O按逆时针方向旋转后,
顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
B
O
C
A
D
B
O
C
A
D
E
F
作法:(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF就是所求作的三角形,如图所示.
M
N
4. 思考:怎样将右边的图案与左边的图案重合?
答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,然后平移,即可得到左边的图案.
课堂小结
作旋转图形
作图基本步骤五步
确定旋转中心
找两条对应点连线段的垂直平分线的交点
旋转的作图
23.1 第2课时 旋转作图
第二十三章 旋转
知识回顾
回顾平移的特征
A
B
C
D
E
F
G
H
K
L
M
N
回顾旋转的特征
O
︵
A
B
C
D
E
F
获取新知
知识一:简单的旋转作图
画一画:如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.线段AC为所求.
A
B
X
C
画出下图所示的四边形 ABCD 以 O为中心,顺时针旋转 60°的旋转图形.
A
B
C
D
O
动手一试
B'
A'
C'
D'
(1)定:明确旋转三要素:
旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
(2)找:找出原图的关键点;
(3)作:作出关键点的对应点;
(4)连:连接对应点作出新图形;
(5)写:写出结论.
归纳总结
例题讲解
例 如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能画出旋转后的图形吗?试一试你有几种方法?
A
B
C
E
D
方法1: 解:∵点A是旋转中心,
∴它的对应点是它本身.
正方形ABCD中,AD=AB,
∠DAB= ,所以旋转后点D与点__ 重合. 设点E的对应点为E′.
∵△ADE △ABE′
∴∠ABE′= = ,
BE′= ,
因此在CB的延长线上截取点E′,使 .
A
B
C
D
E
E ′
90 °
≌
∠ADE
90 °
DE
BE′=DE
则△ABE′为旋转后的图形.
B
体现的SAS的三角形全等的判定方法
(基本作图:作线段)
E'
A
B
C
E
D
方法2:
体现的HL的直角三角形全等的判定方法
(基本作图:作线段)
方法3:
F
A
B
C
E
D
体现的HL的直角三角形全等的判定方法
(基本作图:作线段)
F
A
B
C
E
D
方法4:
┐
体现的ASA的三角形全等的判定方法
(基本作图:作垂线)
(1)旋转中心不变,改变旋转角(如图).
问题 让我们一起来欣赏一下美丽的图案,体会
一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
O
O
β
α
知识二:旋转设计作图
获取新知
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
(3)美丽的图案是这样形成的.
1.如图,该图形围绕点O按下列角度旋转后,不能与自身重合的是( )
A.72° B.108°
C.144° D.216°
B
随堂演练
2. 下列图案中,可以由一个“基本图案”连续旋转45°得到的是( )
C
3. 如图,△ABC绕点O按逆时针方向旋转后,
顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
B
O
C
A
D
B
O
C
A
D
E
F
作法:(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF就是所求作的三角形,如图所示.
M
N
4. 思考:怎样将右边的图案与左边的图案重合?
答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,然后平移,即可得到左边的图案.
课堂小结
作旋转图形
作图基本步骤五步
确定旋转中心
找两条对应点连线段的垂直平分线的交点
旋转的作图
同课章节目录
