人教版九年级上册 23.2.2 中心对称图形 课件(共17张PPT)
文档属性
| 名称 | 人教版九年级上册 23.2.2 中心对称图形 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
23.2.2 中心对称图形
第二十三章 旋转
情景导入
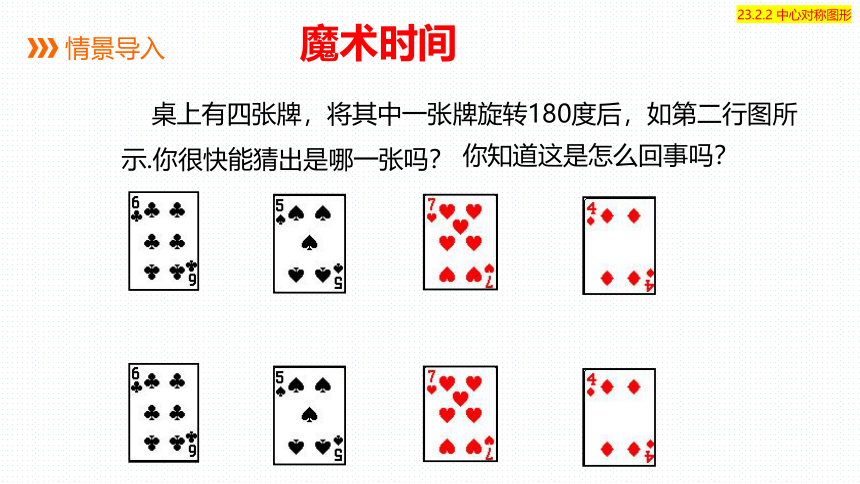
魔术时间
桌上有四张牌,将其中一张牌旋转180度后,如第二行图所示.你很快能猜出是哪一张吗?
你知道这是怎么回事吗?
获取新知
(1)如果将线段AB 绕它的中点O 旋转180°,会出现什么情况?
知识点一:探究中心对称图形的概念
A
B
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
O
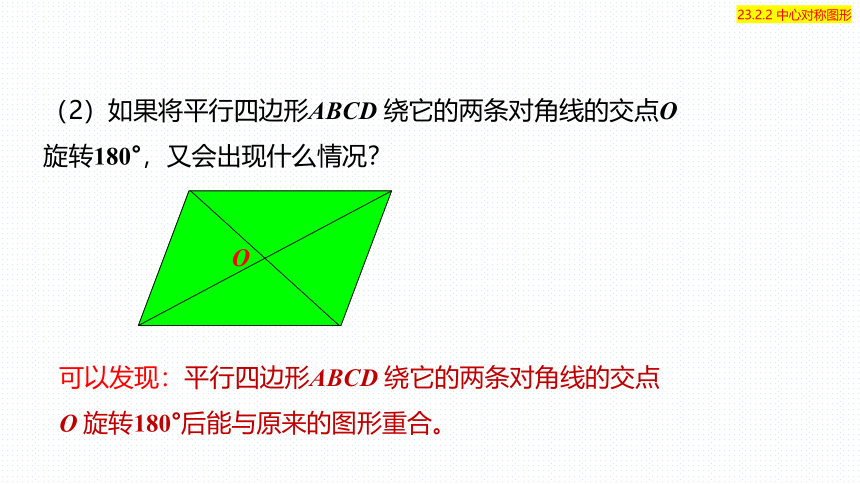
(2)如果将平行四边形ABCD 绕它的两条对角线的交点O旋转180°,又会出现什么情况?
可以发现:平行四边形ABCD 绕它的两条对角线的交点O 旋转180°后能与原来的图形重合。
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形. 这个点就是它的对称中心.
!注意
中心对称图形是指一个图形而言的,中心对称是指两个图形而言的.
知识要点
中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区 别
联 系 (1)是针对2个图形而言的
(1)是针对1个图形而言的
(2)是指两个图形的(位置)关系
(2)是指具有某种性质的一个图形
(3)对称点在两个图形上
(4)对称中心在两个图形之间
(3)对称点在一个图形上
(4)对称中心在图形上或其内部
若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
生活中“美丽”的中心对称图形
例题讲解
例1 判断下列图形是否为中心对称图形.
(1)
(9)
(8)
(7)
(6)
(5)
(4)
(3)
(2)
解:(1)(3)(5)(6)(9)是中心对称图形,
(2)(4)(7)(8)不是中心对称图形.
例2(1)选取1个涂上阴影,使4个阴影小正
方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取1个涂上阴影,使4个阴影小正方形组成一个既是轴对称图形,又是中心对称图形.
知识点三:中心对称图形的性质
获取新知
根据中心对称图形的定义,可知:
1.中心对称图形上的每一对对应点所连线段必经过对称中心,且被对称中心平分;
2.过中心对称图形对称中心的直线将图形分成全等的两部分.
例3 如图,有一个平行四边形请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎么画?
过对称中心的直线可以把中心对称图形分成面积相等的两部分.
归纳
例题讲解
随堂演练
1.下列几个交通标志,其中是中心对称图形的是( )
A B C D
D
2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.等腰三角形
C.平行四边形 D.正方形
D
3. 请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 .
①②③
①③
一石激起千层浪
①
汽车方向盘
②
铜钱
③
4.图中网格中有一个四边形和两个三角形,
(1)请你先画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,则至少旋转多少度才能与自身重合
O
至少旋转90度与自身重合
课堂小结
中心对称图形
定义
性质
应用
绕着内部一点旋转180度能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
23.2.2 中心对称图形
第二十三章 旋转
情景导入
魔术时间
桌上有四张牌,将其中一张牌旋转180度后,如第二行图所示.你很快能猜出是哪一张吗?
你知道这是怎么回事吗?
获取新知
(1)如果将线段AB 绕它的中点O 旋转180°,会出现什么情况?
知识点一:探究中心对称图形的概念
A
B
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
O
(2)如果将平行四边形ABCD 绕它的两条对角线的交点O旋转180°,又会出现什么情况?
可以发现:平行四边形ABCD 绕它的两条对角线的交点O 旋转180°后能与原来的图形重合。
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形. 这个点就是它的对称中心.
!注意
中心对称图形是指一个图形而言的,中心对称是指两个图形而言的.
知识要点
中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区 别
联 系 (1)是针对2个图形而言的
(1)是针对1个图形而言的
(2)是指两个图形的(位置)关系
(2)是指具有某种性质的一个图形
(3)对称点在两个图形上
(4)对称中心在两个图形之间
(3)对称点在一个图形上
(4)对称中心在图形上或其内部
若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
生活中“美丽”的中心对称图形
例题讲解
例1 判断下列图形是否为中心对称图形.
(1)
(9)
(8)
(7)
(6)
(5)
(4)
(3)
(2)
解:(1)(3)(5)(6)(9)是中心对称图形,
(2)(4)(7)(8)不是中心对称图形.
例2(1)选取1个涂上阴影,使4个阴影小正
方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取1个涂上阴影,使4个阴影小正方形组成一个既是轴对称图形,又是中心对称图形.
知识点三:中心对称图形的性质
获取新知
根据中心对称图形的定义,可知:
1.中心对称图形上的每一对对应点所连线段必经过对称中心,且被对称中心平分;
2.过中心对称图形对称中心的直线将图形分成全等的两部分.
例3 如图,有一个平行四边形请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎么画?
过对称中心的直线可以把中心对称图形分成面积相等的两部分.
归纳
例题讲解
随堂演练
1.下列几个交通标志,其中是中心对称图形的是( )
A B C D
D
2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.等腰三角形
C.平行四边形 D.正方形
D
3. 请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 .
①②③
①③
一石激起千层浪
①
汽车方向盘
②
铜钱
③
4.图中网格中有一个四边形和两个三角形,
(1)请你先画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,则至少旋转多少度才能与自身重合
O
至少旋转90度与自身重合
课堂小结
中心对称图形
定义
性质
应用
绕着内部一点旋转180度能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
同课章节目录
