(2022秋季新教材)五年级数学上册6.7 组合图形的面积 课件(共20张PPT)
文档属性
| 名称 | (2022秋季新教材)五年级数学上册6.7 组合图形的面积 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 21:24:36 | ||
图片预览








文档简介
(共20张PPT)
2022秋 人教数学
五年级上册
多边形的面积
6
组合图形的面积
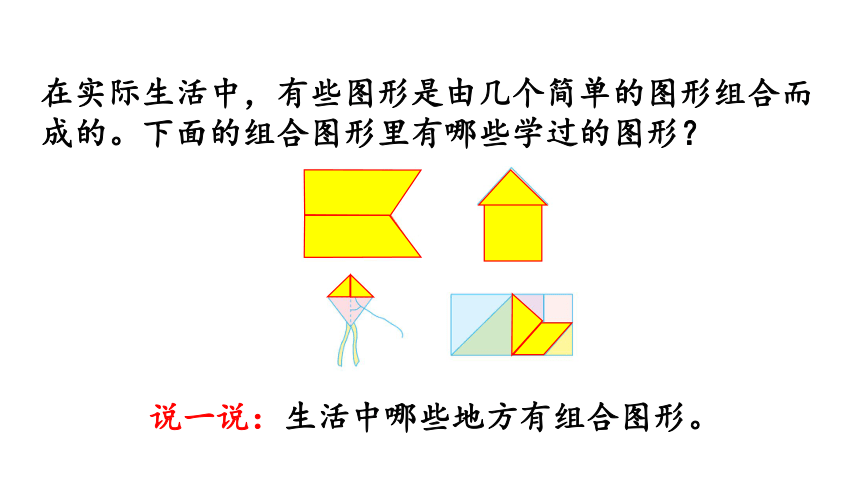
在实际生活中,有些图形是由几个简单的图形组合而成的。下面的组合图形里有哪些学过的图形?
说一说:生活中哪些地方有组合图形。
组合图形:
由几个简单的图形组合而成的图形叫做组合图形。
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
例题4
小组合作:
在图上画出你们的思路,再求出面积,看哪一组的方法最多。
方法一:三角形 + 正方形
三角形面积 = 5×2÷2 = 5 (m2)
正方形面积 = 5×5 = 25 (m2)
房子侧面面积 = 25 + 5 = 30 (m2)
梯形面积 =(5+2+5)×(5÷2) ÷2
= 12×2.5÷2
= 30÷2
= 15 (m2)
房子侧面面积 = 15×2 = 30 (m2)
方法二:两个梯形
长方形面积 = 5×(5+2÷2)
= 5×6
= 30(m2)
房子侧面面积 = 长方形面积
方法三:拼成一个长方形
长方形面积 =(5+2) ×5
= 7×5
= 35 (m2)
两个三角形面积 = 5×2÷2 = 5(m2)
房子侧面面积 = 35 - 5 = 30(m2)
方法四:从长方形中挖走两个小三角形
说一说:求组合图形面积的方法。
方法一
方法二
方法三
方法四
解决组合图形的面积可以采取三种方法,就是分、拼、挖。
我们可以把一个组合图形分成几个
基本图形,也可以运用割补法把一个组
合图形拼成学过的图形,还可以从一个
学过的图形中挖去一部分。
组合图形的面积可以采取分、拼、挖的方法。
把组合图形分成正方形和三角形最好。
如图:已知长方形的长是8 cm,宽是4 cm,A、B两点分别为长方形长、宽上的中点,求阴影部分的面积是多少平方厘米?
用什么方法解决这道题,看谁的方法最巧妙?
A
B
方法一:挖的方法
8×4 = 32(cm2)
(8÷2) ×4÷2 = 8(cm2)
(8÷2) ×(4÷2) = 4×2= 8(cm2)
(4÷2) ×8÷2 = 8(cm2)
32-8-8-8 = 8(cm2)
A
B
方法二:分的方法
(4÷2) ×(8÷2) ÷2
= 2×4÷2
= 4 (cm2)
(8÷2) ×(4÷2) ÷2
= 4×2÷2
= 4(cm2)
4 + 4 = 8(cm2)
A
B
①
②
A
B
(8÷2) ×(4÷2)
= 4×2
= 8(cm2)
方法三:拼的方法
A
B
在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
用什么方法解决这道题?
(70+40) ×30÷2-30×15
= 110×30÷2-450
= 3300÷2-450
= 1650-450
= 1200(m2)
挖的方法
答:草地的面积是 1200 平方米。
用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
方法一: 3×4+(4+10)×(8-3)÷2
=12+35
=47(平方厘米)
方法二: 8×4+(8-3)×(10-4)÷2
=32+15
=47(平方厘米)
方法三: 8×10-(8+3)×(10-4)÷2
=80-33
=47(平方厘米)
方法四: (8+3)×4÷2+(8-3)×10÷2
=22+25
=47(平方厘米)
用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
这节课你们都学会了哪些知识?
组合图形的面积
解决组合图形的面积可以采取三种方法,就是分、拼、挖。
“分”
“拼”
“挖”
2022秋 人教数学
五年级上册
多边形的面积
6
组合图形的面积
在实际生活中,有些图形是由几个简单的图形组合而成的。下面的组合图形里有哪些学过的图形?
说一说:生活中哪些地方有组合图形。
组合图形:
由几个简单的图形组合而成的图形叫做组合图形。
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
例题4
小组合作:
在图上画出你们的思路,再求出面积,看哪一组的方法最多。
方法一:三角形 + 正方形
三角形面积 = 5×2÷2 = 5 (m2)
正方形面积 = 5×5 = 25 (m2)
房子侧面面积 = 25 + 5 = 30 (m2)
梯形面积 =(5+2+5)×(5÷2) ÷2
= 12×2.5÷2
= 30÷2
= 15 (m2)
房子侧面面积 = 15×2 = 30 (m2)
方法二:两个梯形
长方形面积 = 5×(5+2÷2)
= 5×6
= 30(m2)
房子侧面面积 = 长方形面积
方法三:拼成一个长方形
长方形面积 =(5+2) ×5
= 7×5
= 35 (m2)
两个三角形面积 = 5×2÷2 = 5(m2)
房子侧面面积 = 35 - 5 = 30(m2)
方法四:从长方形中挖走两个小三角形
说一说:求组合图形面积的方法。
方法一
方法二
方法三
方法四
解决组合图形的面积可以采取三种方法,就是分、拼、挖。
我们可以把一个组合图形分成几个
基本图形,也可以运用割补法把一个组
合图形拼成学过的图形,还可以从一个
学过的图形中挖去一部分。
组合图形的面积可以采取分、拼、挖的方法。
把组合图形分成正方形和三角形最好。
如图:已知长方形的长是8 cm,宽是4 cm,A、B两点分别为长方形长、宽上的中点,求阴影部分的面积是多少平方厘米?
用什么方法解决这道题,看谁的方法最巧妙?
A
B
方法一:挖的方法
8×4 = 32(cm2)
(8÷2) ×4÷2 = 8(cm2)
(8÷2) ×(4÷2) = 4×2= 8(cm2)
(4÷2) ×8÷2 = 8(cm2)
32-8-8-8 = 8(cm2)
A
B
方法二:分的方法
(4÷2) ×(8÷2) ÷2
= 2×4÷2
= 4 (cm2)
(8÷2) ×(4÷2) ÷2
= 4×2÷2
= 4(cm2)
4 + 4 = 8(cm2)
A
B
①
②
A
B
(8÷2) ×(4÷2)
= 4×2
= 8(cm2)
方法三:拼的方法
A
B
在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
用什么方法解决这道题?
(70+40) ×30÷2-30×15
= 110×30÷2-450
= 3300÷2-450
= 1650-450
= 1200(m2)
挖的方法
答:草地的面积是 1200 平方米。
用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
方法一: 3×4+(4+10)×(8-3)÷2
=12+35
=47(平方厘米)
方法二: 8×4+(8-3)×(10-4)÷2
=32+15
=47(平方厘米)
方法三: 8×10-(8+3)×(10-4)÷2
=80-33
=47(平方厘米)
方法四: (8+3)×4÷2+(8-3)×10÷2
=22+25
=47(平方厘米)
用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
这节课你们都学会了哪些知识?
组合图形的面积
解决组合图形的面积可以采取三种方法,就是分、拼、挖。
“分”
“拼”
“挖”
