2022-2023学年人教版八年级数学上册 14.2.1 平方差公式 课件(共18页PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 14.2.1 平方差公式 课件(共18页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览



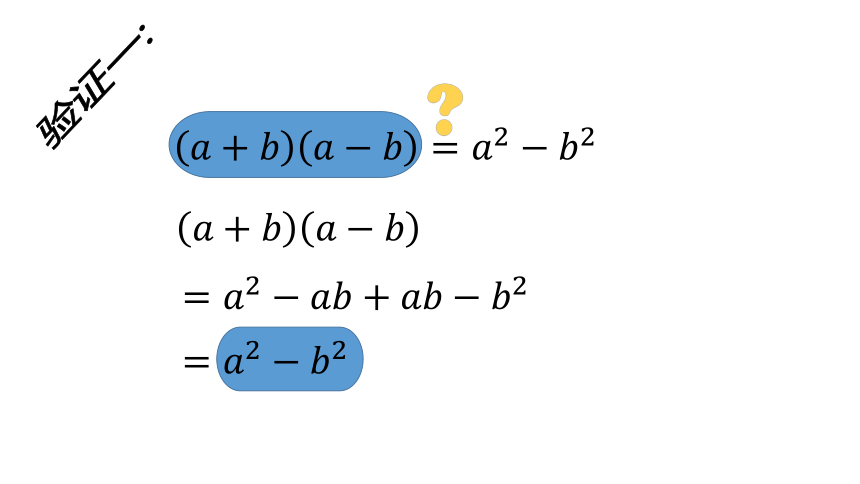


文档简介
(共18张PPT)
14.2.1 平方差公式
导入新课
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
初春时节,小刚的父亲在自家的院子里圈了一块地准备种植新品种黄瓜,这块地是长方形的。他们测得这块地的长是10.2米,宽是9.8米,小刚的父亲要小刚算一下这块地的面积,小刚脱口说出面积是99.96平方米,父亲惊讶的问:“你怎么算得那么快?”小刚说:“我利用了数学课上刚学过的一个公式。”
生活中的数学
验证一:
(1)图中绿色部分的面积为________.
(2)将绿色部分拼成右图的一个长方形,这个长方形的长是 ,宽是,面积是
(3)比较(1)(2)的结果由面积关系可得到:
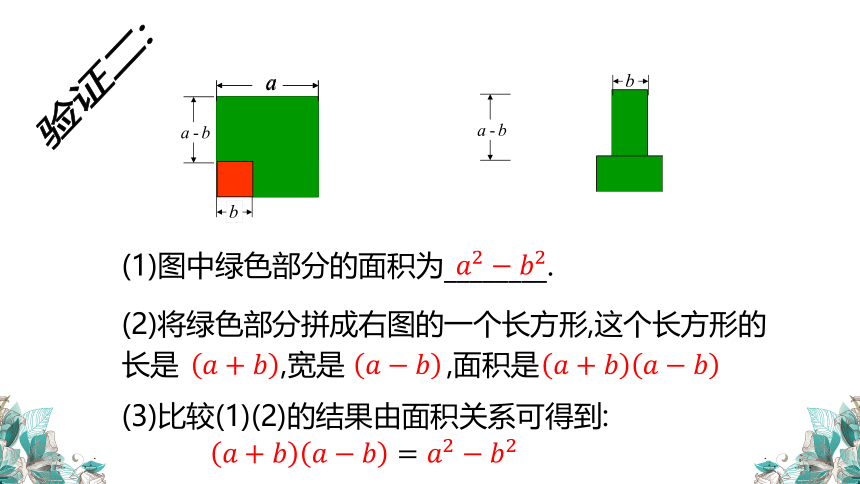
验证二:
①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).
计算下列多项式的积,你能发现什么规律?
算一算:看谁算得又快又准.
知识讲解
②(m+ 2)( m-2)=m2 -22
③(2m+ 1)( 2m-1)=4m2 - 12
④(5y + z)(5y-z)= 25y2 - z2
①(x +1)( x-1)=x2 - 1,
想一想:这些计算结果有什么特点?
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
知识讲解
(a+b)(a b)=
a2 b2
平方差公式
数学表达式: (a+b)(a-b)= a2-b2
智慧升华
文字语言:两数和与这两数差的积,等于它们的平方差。
公式的结构特征
1)结构特征:
a.等号左边是两个二项式相乘,并且有一项完全相同;另一项互为相反数;
b.等号右边是乘式中两项的平方差,即( 符号相同项 )2 - (符号相反项 )2
2)符号特点:
左右两边都有求差运算(分清分清公式中的a,b,是应用公式的关键 )
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
知识讲解
( a + b )( a – b ) = ( a )2 - ( b )2
相反项为b
合理加括号
适当交换位置
相同项为a
3.公式变形: (1)(a-b) (a+b)= a2-b2(位置交换)
(2)(b+a) (-b+a)=a2-b2(因式中加数交换)
智慧升华
温馨提示:
1,字母的代表性:a、b可以是数,还可以是单项式或多项式
2,乘式必须具备公式左边的结构特点,(即 形如“两数和乘以 这两数差)才能应用公式。
下面多项式相乘,哪些能用平方差公式,哪些不能用,如能用公式请找出公式中的a,b
1. (2x+3y) (2x-3y)
2. (2x-3y) (3y-2x)
3. (2x-3y) (2x-3y)
4. (-2x+3y) (2x+3y)
能
能
不能
小试牛刀
不能
判断下列算式能否利用平方差公式计算,若能,计算出它的结果;若不能,怎么办?
(1)(x-1)(x+1)
(2)(-a+b)(a-b)
(3)(2y-2)(2y+3)
(4)(-b-5)(b-5)
(5)(a+b+c)(a+b c)
辨一辨:
(不能)
(能)
(不能)
(能)
(能)
例:用平方差公式计算
(1) (x+2y)(x-2y)
(2) (2y-x)(-2y-x).
学以致用
解:(1)原式=x2-2y2=x2 - 2y2
(2)原式= (-x+2y)(-x-2y) = -x2+(2y)2=-x2+4y2
正确解法
解:(1)(x+2y)(x-2y)=x2-(2y)2=x2 - 4y2
(a+b)(a-b)=a2 - b2
(2)(2y-x)(-2y-x).=(-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2
注意:
1、先把要计算的式子与公式对照;
2、弄清哪个是a哪个是 b是计算的关键.
(b+a)(-b+a)= (a+ b) (a - b) = a2 - b2
例 运用平方差公式计算
(1)
(2)
解:(2)
(1)(2x+3)(2x-3)
(2)(b+2a)(2a-b)
(3)( x+1)( x 1)
运用平方差公式计算
巩固练习
答疑解难
问题:小聪同学去商店买了单价是9.8元/千克的糖块10.2千克,售货员刚拿起计算器,小聪就说出“99.96元”,售货员惊讶地问:“这位同学,你怎么算得这么快 ”小聪同学说:“我利用了在数学上刚学过的一个公式。”你知道小聪同学用的是一个什么样的公式吗
(2)(a-2) (a+2) (a2 + 4)
拓展提升
(1) 20122 -2011×2013
小结
1、平方差公式
(a+b)(a b)=a2 b2
2、运用平方差公式的步骤:先比形式,再套公式.
14.2.1 平方差公式
导入新课
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
初春时节,小刚的父亲在自家的院子里圈了一块地准备种植新品种黄瓜,这块地是长方形的。他们测得这块地的长是10.2米,宽是9.8米,小刚的父亲要小刚算一下这块地的面积,小刚脱口说出面积是99.96平方米,父亲惊讶的问:“你怎么算得那么快?”小刚说:“我利用了数学课上刚学过的一个公式。”
生活中的数学
验证一:
(1)图中绿色部分的面积为________.
(2)将绿色部分拼成右图的一个长方形,这个长方形的长是 ,宽是,面积是
(3)比较(1)(2)的结果由面积关系可得到:
验证二:
①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).
计算下列多项式的积,你能发现什么规律?
算一算:看谁算得又快又准.
知识讲解
②(m+ 2)( m-2)=m2 -22
③(2m+ 1)( 2m-1)=4m2 - 12
④(5y + z)(5y-z)= 25y2 - z2
①(x +1)( x-1)=x2 - 1,
想一想:这些计算结果有什么特点?
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
知识讲解
(a+b)(a b)=
a2 b2
平方差公式
数学表达式: (a+b)(a-b)= a2-b2
智慧升华
文字语言:两数和与这两数差的积,等于它们的平方差。
公式的结构特征
1)结构特征:
a.等号左边是两个二项式相乘,并且有一项完全相同;另一项互为相反数;
b.等号右边是乘式中两项的平方差,即( 符号相同项 )2 - (符号相反项 )2
2)符号特点:
左右两边都有求差运算(分清分清公式中的a,b,是应用公式的关键 )
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
知识讲解
( a + b )( a – b ) = ( a )2 - ( b )2
相反项为b
合理加括号
适当交换位置
相同项为a
3.公式变形: (1)(a-b) (a+b)= a2-b2(位置交换)
(2)(b+a) (-b+a)=a2-b2(因式中加数交换)
智慧升华
温馨提示:
1,字母的代表性:a、b可以是数,还可以是单项式或多项式
2,乘式必须具备公式左边的结构特点,(即 形如“两数和乘以 这两数差)才能应用公式。
下面多项式相乘,哪些能用平方差公式,哪些不能用,如能用公式请找出公式中的a,b
1. (2x+3y) (2x-3y)
2. (2x-3y) (3y-2x)
3. (2x-3y) (2x-3y)
4. (-2x+3y) (2x+3y)
能
能
不能
小试牛刀
不能
判断下列算式能否利用平方差公式计算,若能,计算出它的结果;若不能,怎么办?
(1)(x-1)(x+1)
(2)(-a+b)(a-b)
(3)(2y-2)(2y+3)
(4)(-b-5)(b-5)
(5)(a+b+c)(a+b c)
辨一辨:
(不能)
(能)
(不能)
(能)
(能)
例:用平方差公式计算
(1) (x+2y)(x-2y)
(2) (2y-x)(-2y-x).
学以致用
解:(1)原式=x2-2y2=x2 - 2y2
(2)原式= (-x+2y)(-x-2y) = -x2+(2y)2=-x2+4y2
正确解法
解:(1)(x+2y)(x-2y)=x2-(2y)2=x2 - 4y2
(a+b)(a-b)=a2 - b2
(2)(2y-x)(-2y-x).=(-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2
注意:
1、先把要计算的式子与公式对照;
2、弄清哪个是a哪个是 b是计算的关键.
(b+a)(-b+a)= (a+ b) (a - b) = a2 - b2
例 运用平方差公式计算
(1)
(2)
解:(2)
(1)(2x+3)(2x-3)
(2)(b+2a)(2a-b)
(3)( x+1)( x 1)
运用平方差公式计算
巩固练习
答疑解难
问题:小聪同学去商店买了单价是9.8元/千克的糖块10.2千克,售货员刚拿起计算器,小聪就说出“99.96元”,售货员惊讶地问:“这位同学,你怎么算得这么快 ”小聪同学说:“我利用了在数学上刚学过的一个公式。”你知道小聪同学用的是一个什么样的公式吗
(2)(a-2) (a+2) (a2 + 4)
拓展提升
(1) 20122 -2011×2013
小结
1、平方差公式
(a+b)(a b)=a2 b2
2、运用平方差公式的步骤:先比形式,再套公式.
