2022-2023学年人教版八年级数学上册 14.3.2 公式法 课件(共17页PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 14.3.2 公式法 课件(共17页PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 19:28:32 | ||
图片预览


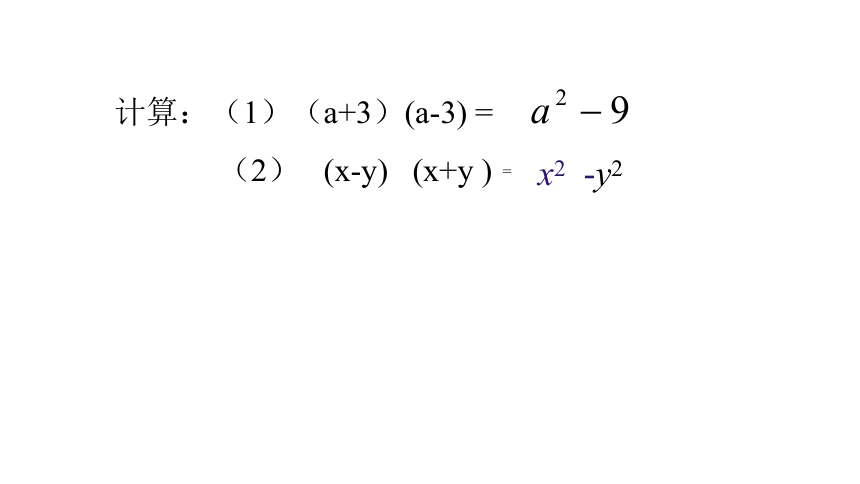




文档简介
(共17张PPT)
14.3.2 公式法
2、判断下列变形过程,哪些是因式分解
(1) 7m-7n-7=7(m-n-1) ( )
(2) 4x2- 9 =(2x+3)(2x- 3 ) ( )
(3) (a+b)(a-b)=a2- b2 ( )
√
√
1:什么叫多项式的因式分解
把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解
复习回顾:
×
计算:(1)(a+3)(a-3) =
(2) (x-y) (x+y )
x2 -y2
=
a - b = ( )( )
你能将多项式 a2 - b2 进行因式分解吗?
二、尝试分解
a+b
a-b
。
答:等式左边:
1. 多项式只有两项,两项符号相反
2.两项都可写某个式子(或数)的平方
因式分解的平方差公式:
a - b = (a+b) (a-b)
1、用语言叙述这个公式.
2、仔细地从等式的左边研究一下多项式满足什么特征
3、等式的右边的特点?
等式右边:两个数(式)的和与这两个 数(式)的差的积
火眼金睛
下列多项式能否用平方差公式来分解因式?
(1) x2 + y2
(2) x2 - y2
(3) -x2+y2
(4) -x2 - y2
不能
能
能
不能
二、探究新知
例1 试对下列多项式进行因式分解:
(1)4x2-9;
(2)(x+p)2-(x+q) 2.
尝试应用
分析:(1)这些多项式的共同特征都是“平方差”的形式,都可化为( )2 -( )2.
(2)最后结果都化成积的形式,即( )( ).
二、探究新知
注意:
(1)因式分解要进行到不能再分解为止.
(2)仔细分析题目特征,灵活运用公式法或提取公因式法
例2. 分解因式:
(1) x4-y4;
(2)a3b-ab;
(3)(3x2+2y2)2-(2x2+3y2)2.
尝试应用
除了平方差公式外,还学过了哪些公式?
回顾&思考
现在我们把乘法公式反过来,可得:
概念理解
形如 的式子称为完全平方式.
从左到右的过程是不是因式分解呢?
判断下列各式是不是完全平方式.
巩固概念
(1)
(2)
(3)
(4)
(5)
(6)
是
是
不是
不是
是
不是
小组合作:如何判断一个多项式是不是完全平方式?请你从以下三方面总结完全平方式的特点.(①项数;②每一项特点;③符号.)
①多项式为三项式;
②首末项是平方且符号相同;
③中间项是乘积2倍,符号 正负均可;
④a和b可以表示数、单项式或多项式.
例1 把下列完全平方式因式分解:
学以致用
(1)
解:
(2)
解:
把(m+n)看作整体!
这是个二次三项式,有两个数的平方和还有加减这两个数积的2倍就可以化成右边的两数和(或差)的平方.
完全平方公式的结构特点是什么?
还要注意:
当多项式各项有公因式时,应该首先考虑提公因式,然后再运用公式分解
有些情况下,多项式不能直接用公式,需要先进行适当的组合、变形、整体代换。
利用平方差公式因式分解。
随堂演练
随堂演练
把下列完全平方式因式分解:
(1)
(2)
(3)
随堂演练
请你任选一组进行因式分解.
(1)
(2)
A组
(1)
(2)
B组
你能否与做另一组题的同学互换批改订正呢?
(1)
(2)
A组
(1)
(2)
B组
14.3.2 公式法
2、判断下列变形过程,哪些是因式分解
(1) 7m-7n-7=7(m-n-1) ( )
(2) 4x2- 9 =(2x+3)(2x- 3 ) ( )
(3) (a+b)(a-b)=a2- b2 ( )
√
√
1:什么叫多项式的因式分解
把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解
复习回顾:
×
计算:(1)(a+3)(a-3) =
(2) (x-y) (x+y )
x2 -y2
=
a - b = ( )( )
你能将多项式 a2 - b2 进行因式分解吗?
二、尝试分解
a+b
a-b
。
答:等式左边:
1. 多项式只有两项,两项符号相反
2.两项都可写某个式子(或数)的平方
因式分解的平方差公式:
a - b = (a+b) (a-b)
1、用语言叙述这个公式.
2、仔细地从等式的左边研究一下多项式满足什么特征
3、等式的右边的特点?
等式右边:两个数(式)的和与这两个 数(式)的差的积
火眼金睛
下列多项式能否用平方差公式来分解因式?
(1) x2 + y2
(2) x2 - y2
(3) -x2+y2
(4) -x2 - y2
不能
能
能
不能
二、探究新知
例1 试对下列多项式进行因式分解:
(1)4x2-9;
(2)(x+p)2-(x+q) 2.
尝试应用
分析:(1)这些多项式的共同特征都是“平方差”的形式,都可化为( )2 -( )2.
(2)最后结果都化成积的形式,即( )( ).
二、探究新知
注意:
(1)因式分解要进行到不能再分解为止.
(2)仔细分析题目特征,灵活运用公式法或提取公因式法
例2. 分解因式:
(1) x4-y4;
(2)a3b-ab;
(3)(3x2+2y2)2-(2x2+3y2)2.
尝试应用
除了平方差公式外,还学过了哪些公式?
回顾&思考
现在我们把乘法公式反过来,可得:
概念理解
形如 的式子称为完全平方式.
从左到右的过程是不是因式分解呢?
判断下列各式是不是完全平方式.
巩固概念
(1)
(2)
(3)
(4)
(5)
(6)
是
是
不是
不是
是
不是
小组合作:如何判断一个多项式是不是完全平方式?请你从以下三方面总结完全平方式的特点.(①项数;②每一项特点;③符号.)
①多项式为三项式;
②首末项是平方且符号相同;
③中间项是乘积2倍,符号 正负均可;
④a和b可以表示数、单项式或多项式.
例1 把下列完全平方式因式分解:
学以致用
(1)
解:
(2)
解:
把(m+n)看作整体!
这是个二次三项式,有两个数的平方和还有加减这两个数积的2倍就可以化成右边的两数和(或差)的平方.
完全平方公式的结构特点是什么?
还要注意:
当多项式各项有公因式时,应该首先考虑提公因式,然后再运用公式分解
有些情况下,多项式不能直接用公式,需要先进行适当的组合、变形、整体代换。
利用平方差公式因式分解。
随堂演练
随堂演练
把下列完全平方式因式分解:
(1)
(2)
(3)
随堂演练
请你任选一组进行因式分解.
(1)
(2)
A组
(1)
(2)
B组
你能否与做另一组题的同学互换批改订正呢?
(1)
(2)
A组
(1)
(2)
B组
