2022-2023学年人教版八年级数学上册15.1.1 从分数到分式 课件(共17张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册15.1.1 从分数到分式 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 21:21:49 | ||
图片预览



文档简介
(共17张PPT)
15.1.1 从分数到分式
学习目标:
1、理解并掌握分式的概念,能用分式表示数量关系;
2、能够正确区分整式和分式;
3、能熟练求出分式有意义、无意义及分式值为零的条件.
(1)正 n 边形的每个外角为________度
(2)一箱水果售价 a 元,箱子与水果的总质量为 m kg,箱子的质量为 n kg,则每千克水果的售价是_______元
做一做
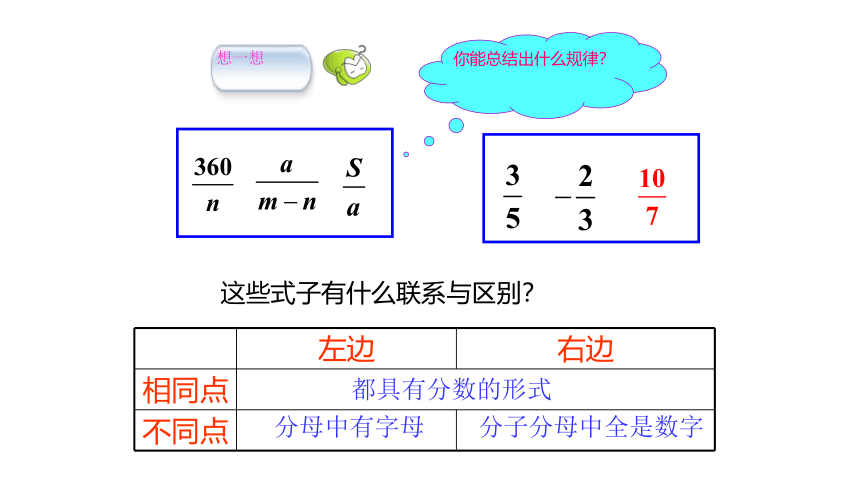
左边 右边
相同点 不同点
这些式子有什么联系与区别?
你能总结出什么规律?
都具有分数的形式
分母中有字母
分子分母中全是数字
想一想
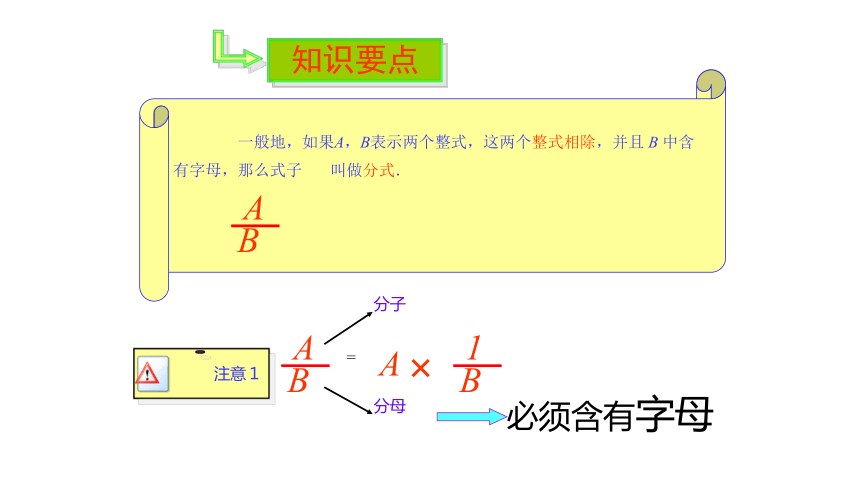
一般地,如果A,B表示两个整式,这两个整式相除,并且 B 中含有字母,那么式子 叫做分式.
A
B
A
B
分子
分母
=
1
B
A
×
必须含有字母
知识要点
注意1
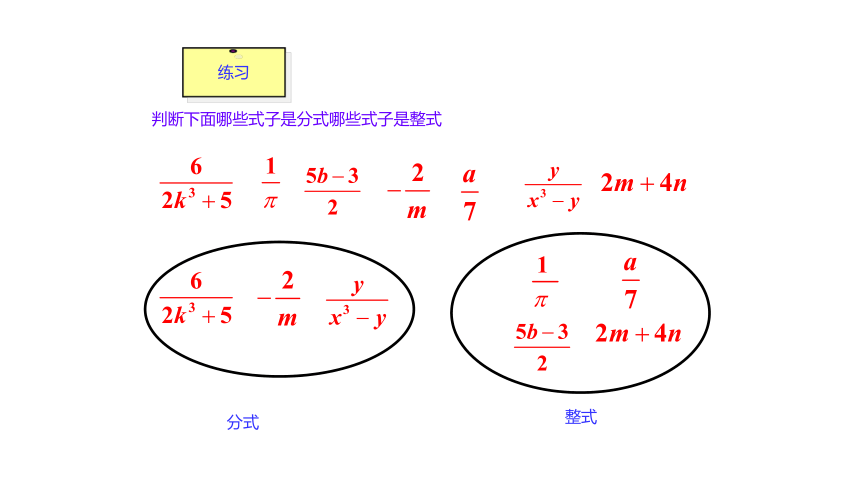
判断下面哪些式子是分式哪些式子是整式
分式
整式
练习
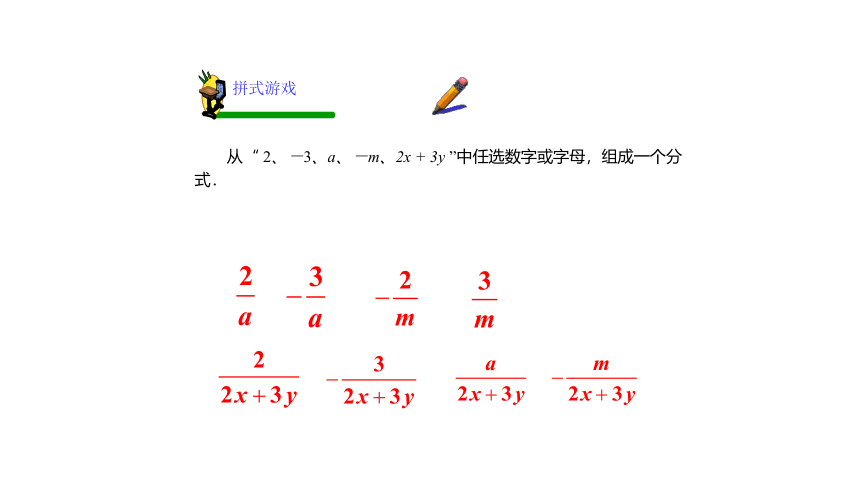
从“ 2、-3、a、-m、2x + 3y ”中任选数字或字母,组成一个分式.
拼式游戏
A
B
在分式的概念中,隐含了一个条件,你知道吗?
分式中,分母可以取任意实数吗
在分数中,分母不能为0 !
提示
想一想
分式的分母为不能为0的实数,分子可以是任意实数。
结论:
【例题1】
指出下列代数式中,哪些是整式,哪些是分式?
解:整式有:(3),(5),(6)
分式有:(1),(2),(4)
知识点1
分式的概念
例题2:下列式子中,哪些是分式?哪些是整式?
解:
分式有①③④⑥;整式有②⑤.
知识点1
分式的概念
【例题3】
请你用所给的代数式,尽可能多地构造出分式:a,5,a-2,π.
分式的概念
知识点1
【规律总结】分式 辨别的“两关键”和“两误区”
1.“两关键”:
(1) 的形式(A,B都是整式).
(2)B中必须含有字母.
2.“两误区”:
(1)含分母的不一定是分式,如分母是数或π.
(2)只看形式,不能看化简后的结果,如 是分式,而不是整式.
例 4 下列分式中的字母满足什么条件时分式有意义?
解:(1)要使分式 有意义,则分母 x-1 ≠0 ,
即 x ≠ 1;
知识点2
分式有意义的条件
当x为任意实数时,下列分式一定有意义的是( )
想一想
知识点2
分式有意义的条件
C
2.使分式 有意义,则x的取值范围是( )
A.
B.
C.
D.
试一试
1.若分式: 有意义,则( )
A.x≠2 B.x≠-3 C.x≠-3或x≠2 D.无法确定
A
D
下列分式中的字母满足什么条件时分式有意义?
a≠0
x≠1
x≠y
b≠3a
x≠±1
检测自学成果
一般地,设A、B分别表示两个整式,A÷B = ,如果B中含有字母,则式子 叫做分式.其中A叫分子,B叫分母。
A
B
A
B
1.分式的基本概念:
课堂小结
今天你学到了什么?
2.分式何时有意义:
只有满足了分式的分母不能为 0 这个条件,分式才有意义。即当B≠0时,分式 才有意义。
15.1.1 从分数到分式
学习目标:
1、理解并掌握分式的概念,能用分式表示数量关系;
2、能够正确区分整式和分式;
3、能熟练求出分式有意义、无意义及分式值为零的条件.
(1)正 n 边形的每个外角为________度
(2)一箱水果售价 a 元,箱子与水果的总质量为 m kg,箱子的质量为 n kg,则每千克水果的售价是_______元
做一做
左边 右边
相同点 不同点
这些式子有什么联系与区别?
你能总结出什么规律?
都具有分数的形式
分母中有字母
分子分母中全是数字
想一想
一般地,如果A,B表示两个整式,这两个整式相除,并且 B 中含有字母,那么式子 叫做分式.
A
B
A
B
分子
分母
=
1
B
A
×
必须含有字母
知识要点
注意1
判断下面哪些式子是分式哪些式子是整式
分式
整式
练习
从“ 2、-3、a、-m、2x + 3y ”中任选数字或字母,组成一个分式.
拼式游戏
A
B
在分式的概念中,隐含了一个条件,你知道吗?
分式中,分母可以取任意实数吗
在分数中,分母不能为0 !
提示
想一想
分式的分母为不能为0的实数,分子可以是任意实数。
结论:
【例题1】
指出下列代数式中,哪些是整式,哪些是分式?
解:整式有:(3),(5),(6)
分式有:(1),(2),(4)
知识点1
分式的概念
例题2:下列式子中,哪些是分式?哪些是整式?
解:
分式有①③④⑥;整式有②⑤.
知识点1
分式的概念
【例题3】
请你用所给的代数式,尽可能多地构造出分式:a,5,a-2,π.
分式的概念
知识点1
【规律总结】分式 辨别的“两关键”和“两误区”
1.“两关键”:
(1) 的形式(A,B都是整式).
(2)B中必须含有字母.
2.“两误区”:
(1)含分母的不一定是分式,如分母是数或π.
(2)只看形式,不能看化简后的结果,如 是分式,而不是整式.
例 4 下列分式中的字母满足什么条件时分式有意义?
解:(1)要使分式 有意义,则分母 x-1 ≠0 ,
即 x ≠ 1;
知识点2
分式有意义的条件
当x为任意实数时,下列分式一定有意义的是( )
想一想
知识点2
分式有意义的条件
C
2.使分式 有意义,则x的取值范围是( )
A.
B.
C.
D.
试一试
1.若分式: 有意义,则( )
A.x≠2 B.x≠-3 C.x≠-3或x≠2 D.无法确定
A
D
下列分式中的字母满足什么条件时分式有意义?
a≠0
x≠1
x≠y
b≠3a
x≠±1
检测自学成果
一般地,设A、B分别表示两个整式,A÷B = ,如果B中含有字母,则式子 叫做分式.其中A叫分子,B叫分母。
A
B
A
B
1.分式的基本概念:
课堂小结
今天你学到了什么?
2.分式何时有意义:
只有满足了分式的分母不能为 0 这个条件,分式才有意义。即当B≠0时,分式 才有意义。
