12.4.1单项式除以单项式 课件(17张PPT)
文档属性
| 名称 | 12.4.1单项式除以单项式 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 12:15:24 | ||
图片预览





文档简介
(共17张PPT)
12.4.1单项式除以单项式
华师大版 八年级上册
教学目标
1.理解掌握单项式除以单项式的法则.
2.会进行单项式除以单项式的运算.
【教学重点】运用单项式除以单项式的法则进行计算.
【教学难点】探求单项式除以单项式的方法.
新知导入
我们知道“先看见闪电,后听到雷声”,那是因为在空气中光的传播速度是3×108m/s,而声音在空气中的传播速度是3.4×102m/s.在空气中光速是声速的多少倍?
(3×108)÷(3.4×102)
(3.4×102)×___________=3×108
想一想
8.8×105
提问:对于一般的两个单项式相除,这种方法可运用吗?
新知讲解
试
一
试
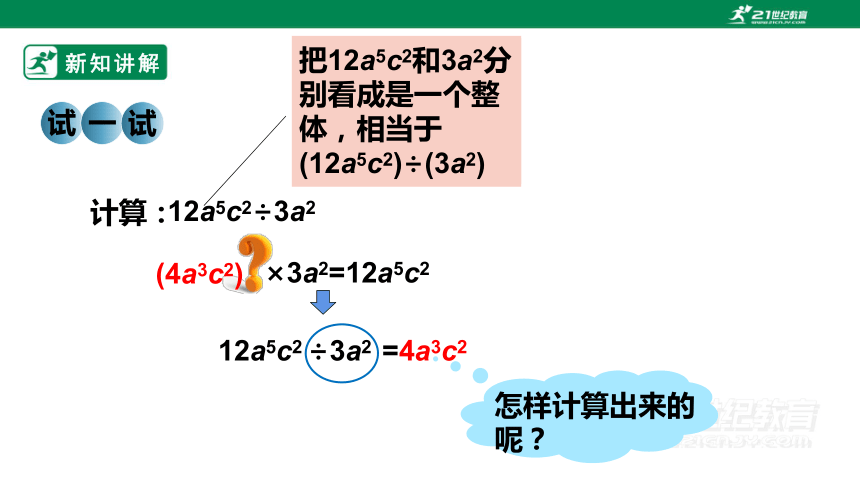
计算:
12a5c2÷3a2
×3a2=12a5c2
把12a5c2和3a2分别看成是一个整体,相当于(12a5c2)÷(3a2)
(4a3c2)
12a5c2 ÷3a2 =4a3c2
怎样计算出来的呢?
典例讲解
例1 计算 :
(1) 24a3b2 ÷3ab2; (2) -21a2b3c÷3ab; (3) (6xy2)2÷3xy.
解:(1) 24a3b2 ÷3ab2
= (24÷3)(a3÷a)(b2÷b2)
= 8a3-1·1
= 8a2
(2) -21a2b3c÷3ab;
=(-21÷3)a2-1b3-1c
= -7ab2c.
(3) (6xy2)2÷3xy.
= 36x2y4÷3xy
= 12xy3
(1)(2)小题的结构一样, 说说可能用到的有关幂的运算公式或法则.
新知讲解
看成是一个整体
12(a-b)5÷3(a-b)2
=(12÷3)[(a-b)5÷(a-b)2]
=4(a-b)5-2
=4(a-b)3
你能用(a-b)的幂表示12(a-b)5÷3(a-b)2的结果吗?
新知讲解
理解
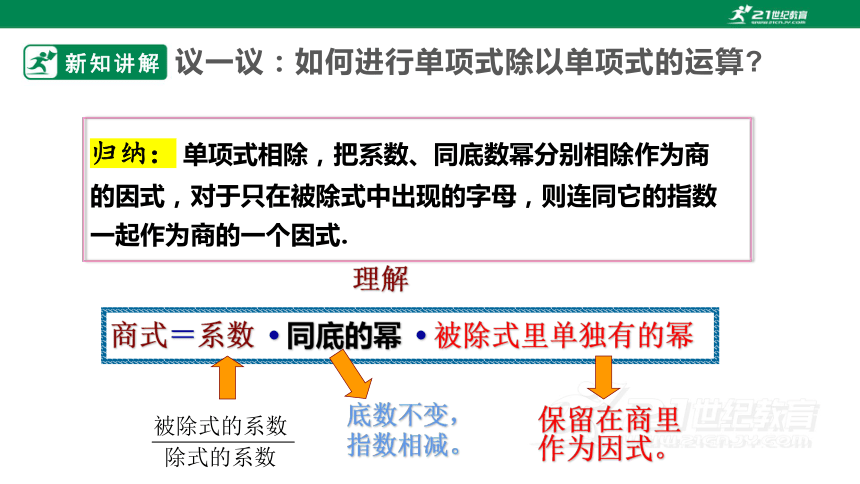
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
归纳: 单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
议一议:如何进行单项式除以单项式的运算
巩固练习
1、填表:
被除式 6x3y3 -42x3y3 -42x3y3
除式 2xy -6x2y2
商 7x3
3x2y2
-6y3
7xy
例题讲解
例2 计算:
1)
(2) (-)
思路分析:
例题讲解
例3 如果 = ,求m、a、b的值
思路分析:
课堂练习
(3) ( )÷(2x3y3 ) = ;
1、计算填空:
⑴ (60x3y5) ÷( 12xy3) = ;
(2) (8x6y4z) ÷( ) = 4x2y2 ;
(4) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;
5x2y2
2x4y2z
12
3
2
课堂练习
2、计算填空:
(1)(3xy2)2· ÷
(2)
课堂练习
3、先化简再求值:
(1) [(xy+2)(xy-2)-2x2y2+4]÷(-xy)其中
解 [(xy+2)(xy-2)-2x2y2+4]÷(-xy)
=(x2y2-4-2x2y2+4)÷(-xy)
=-x2y2÷(-xy)
当x=10,y= 时,
课堂练习
(2) 28(x+y)4(x-2y)5÷[-7(x+y)3(x-2y)4]
解:28(x+y)4(x-2y)5÷[-7(x+y)3(x-2y)4]
=-4(x+y)(x-2y)
=-4x2+4xy+8y2
当x=1,y= 2 时,
课堂总结
本题课你有什么收获或感想?你还有什么疑问?
单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.4.1单项式除以单项式
华师大版 八年级上册
教学目标
1.理解掌握单项式除以单项式的法则.
2.会进行单项式除以单项式的运算.
【教学重点】运用单项式除以单项式的法则进行计算.
【教学难点】探求单项式除以单项式的方法.
新知导入
我们知道“先看见闪电,后听到雷声”,那是因为在空气中光的传播速度是3×108m/s,而声音在空气中的传播速度是3.4×102m/s.在空气中光速是声速的多少倍?
(3×108)÷(3.4×102)
(3.4×102)×___________=3×108
想一想
8.8×105
提问:对于一般的两个单项式相除,这种方法可运用吗?
新知讲解
试
一
试
计算:
12a5c2÷3a2
×3a2=12a5c2
把12a5c2和3a2分别看成是一个整体,相当于(12a5c2)÷(3a2)
(4a3c2)
12a5c2 ÷3a2 =4a3c2
怎样计算出来的呢?
典例讲解
例1 计算 :
(1) 24a3b2 ÷3ab2; (2) -21a2b3c÷3ab; (3) (6xy2)2÷3xy.
解:(1) 24a3b2 ÷3ab2
= (24÷3)(a3÷a)(b2÷b2)
= 8a3-1·1
= 8a2
(2) -21a2b3c÷3ab;
=(-21÷3)a2-1b3-1c
= -7ab2c.
(3) (6xy2)2÷3xy.
= 36x2y4÷3xy
= 12xy3
(1)(2)小题的结构一样, 说说可能用到的有关幂的运算公式或法则.
新知讲解
看成是一个整体
12(a-b)5÷3(a-b)2
=(12÷3)[(a-b)5÷(a-b)2]
=4(a-b)5-2
=4(a-b)3
你能用(a-b)的幂表示12(a-b)5÷3(a-b)2的结果吗?
新知讲解
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
归纳: 单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
议一议:如何进行单项式除以单项式的运算
巩固练习
1、填表:
被除式 6x3y3 -42x3y3 -42x3y3
除式 2xy -6x2y2
商 7x3
3x2y2
-6y3
7xy
例题讲解
例2 计算:
1)
(2) (-)
思路分析:
例题讲解
例3 如果 = ,求m、a、b的值
思路分析:
课堂练习
(3) ( )÷(2x3y3 ) = ;
1、计算填空:
⑴ (60x3y5) ÷( 12xy3) = ;
(2) (8x6y4z) ÷( ) = 4x2y2 ;
(4) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;
5x2y2
2x4y2z
12
3
2
课堂练习
2、计算填空:
(1)(3xy2)2· ÷
(2)
课堂练习
3、先化简再求值:
(1) [(xy+2)(xy-2)-2x2y2+4]÷(-xy)其中
解 [(xy+2)(xy-2)-2x2y2+4]÷(-xy)
=(x2y2-4-2x2y2+4)÷(-xy)
=-x2y2÷(-xy)
当x=10,y= 时,
课堂练习
(2) 28(x+y)4(x-2y)5÷[-7(x+y)3(x-2y)4]
解:28(x+y)4(x-2y)5÷[-7(x+y)3(x-2y)4]
=-4(x+y)(x-2y)
=-4x2+4xy+8y2
当x=1,y= 2 时,
课堂总结
本题课你有什么收获或感想?你还有什么疑问?
单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
