2022-2023学年人教版数学 九年级上册21.2.1 配方法 课件(共18页)
文档属性
| 名称 | 2022-2023学年人教版数学 九年级上册21.2.1 配方法 课件(共18页) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 17:36:36 | ||
图片预览





文档简介
(共18张PPT)
21.2.1 配方法
一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
小练习:用开平方法解下列方程:
(1)3x2-27=0;
(2)(2x-3)2=7
填一填
方程 可以化成 _________ ,
进行降次,得________ ,方程的根
______ , _______ .
问题
要使一块长方形场地的长比宽多6m,并且
面积为16m2,场地的长和宽应各是多少?
设场地的宽为 ,长 ,列方程得
即
移项
两边加9(即 ),使左边配成 的形式
左边写成平方形式
降次
解一次方程
以上解法中,为什么在方程 两边加9?加其他数行吗?
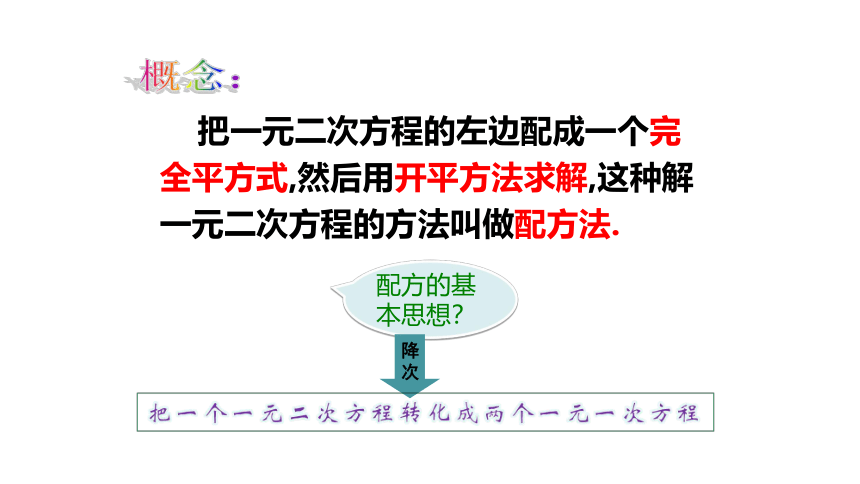
把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
配方的基本思想?
降次
概念:
移项
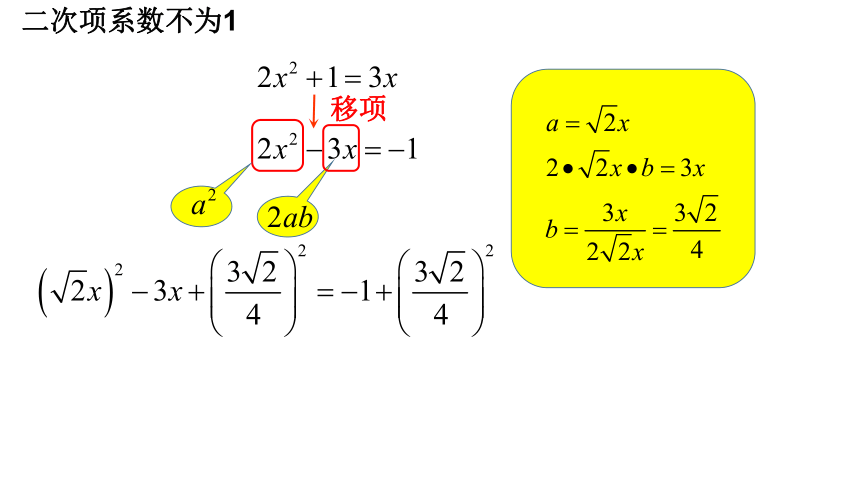
二次项系数不为1
移项
系数化为1
配方
开方
求解
用配方法解一元二次方程步骤
解一元一次方程。
根据平方根意义,方程两边开平方;
方程左边分解因式,右边合并同类;
方程两边都加上一次项系数一半的平方;
1.移项:
2.二次项系数化为 1:
3.配方:
4.变形:
5.开方:
6.求解:
例1 解下列方程:
解:(1)移项,得
x2-8x=-1,
配方,得
x2-8x+42=-1+42 ,
( x-4)2=15
由此可得
即
配方,得
由此可得
二次项系数化为1,得
解:移项,得
2x2-3x=-1,
即
移项和二次项系数化为1这两个步骤能不能交换一下呢
配方,得
因为实数的平方不会是负数,所以x取任何实数时,上式都不成立,所以原方程无实数根.
解:移项,得
二次项系数化为1,得
即
思考
:用配方法解一元二次方程的一般步骤及注意事项
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p.
①当p>0时,则 ,方程的两个根为
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为
x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
规律总结
巩固练习
1.若x2-4x+p=(x+q),那么p,q的值分别是( )
A.p=4,q=2 B.p=4,q=-2
C.p=-4,q=2 D.p=-4,q=-2
2.方程3x2+9=0的根为( )
A.3 B.-3 C.±3 D.无实数根
3.如果方程2(x-3)2=72,那么,这个一元二次方程的两根是 .
4.如果实数a,b满足 +b2-12b+36=0,那么ab的值是 .
D
B
9或-3
-8
5.解关于x的方程.
6.已知方程的一个根是,求m的值即方程的另一个根?
解:当n≥0时,x+m=± ,x1= -m,x2=- -m;当n<0时,无解.
解:将x=4带入(x-2)2=m2-1,得m2-1=4,∴m=± ,故原方程可化为(x-2)2=4,∴x1= 0,x2=4,及另一个根为0.
谈谈你的收获!!
1.一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
2.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
3.对于二次项系数不为1的一元二次方程,
用配方法求解时首先要怎样做 ?
首先要把二次项系数化为1
4.用配方法解一元二次方程的一般步骤:
(1)系数化为1
(2)移项
(3)配方
(4)开方
(5)求解
(6)定根
21.2.1 配方法
一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
小练习:用开平方法解下列方程:
(1)3x2-27=0;
(2)(2x-3)2=7
填一填
方程 可以化成 _________ ,
进行降次,得________ ,方程的根
______ , _______ .
问题
要使一块长方形场地的长比宽多6m,并且
面积为16m2,场地的长和宽应各是多少?
设场地的宽为 ,长 ,列方程得
即
移项
两边加9(即 ),使左边配成 的形式
左边写成平方形式
降次
解一次方程
以上解法中,为什么在方程 两边加9?加其他数行吗?
把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
配方的基本思想?
降次
概念:
移项
二次项系数不为1
移项
系数化为1
配方
开方
求解
用配方法解一元二次方程步骤
解一元一次方程。
根据平方根意义,方程两边开平方;
方程左边分解因式,右边合并同类;
方程两边都加上一次项系数一半的平方;
1.移项:
2.二次项系数化为 1:
3.配方:
4.变形:
5.开方:
6.求解:
例1 解下列方程:
解:(1)移项,得
x2-8x=-1,
配方,得
x2-8x+42=-1+42 ,
( x-4)2=15
由此可得
即
配方,得
由此可得
二次项系数化为1,得
解:移项,得
2x2-3x=-1,
即
移项和二次项系数化为1这两个步骤能不能交换一下呢
配方,得
因为实数的平方不会是负数,所以x取任何实数时,上式都不成立,所以原方程无实数根.
解:移项,得
二次项系数化为1,得
即
思考
:用配方法解一元二次方程的一般步骤及注意事项
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p.
①当p>0时,则 ,方程的两个根为
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为
x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
规律总结
巩固练习
1.若x2-4x+p=(x+q),那么p,q的值分别是( )
A.p=4,q=2 B.p=4,q=-2
C.p=-4,q=2 D.p=-4,q=-2
2.方程3x2+9=0的根为( )
A.3 B.-3 C.±3 D.无实数根
3.如果方程2(x-3)2=72,那么,这个一元二次方程的两根是 .
4.如果实数a,b满足 +b2-12b+36=0,那么ab的值是 .
D
B
9或-3
-8
5.解关于x的方程.
6.已知方程的一个根是,求m的值即方程的另一个根?
解:当n≥0时,x+m=± ,x1= -m,x2=- -m;当n<0时,无解.
解:将x=4带入(x-2)2=m2-1,得m2-1=4,∴m=± ,故原方程可化为(x-2)2=4,∴x1= 0,x2=4,及另一个根为0.
谈谈你的收获!!
1.一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
2.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
3.对于二次项系数不为1的一元二次方程,
用配方法求解时首先要怎样做 ?
首先要把二次项系数化为1
4.用配方法解一元二次方程的一般步骤:
(1)系数化为1
(2)移项
(3)配方
(4)开方
(5)求解
(6)定根
同课章节目录
