2022-2023学年人教版九年级数学上册21.3 实际问题与一元二次方程 课件(共25页)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册21.3 实际问题与一元二次方程 课件(共25页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
21.3 实际问题与一元二次方程
1.分析“传播问题”的特征
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
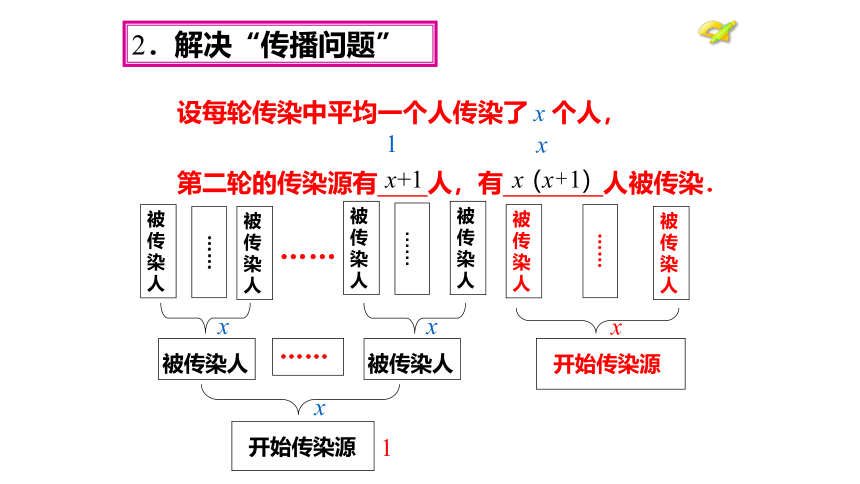
2.解决“传播问题”
探究 有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个
人?
(2)每一轮的传染源和传染之后的患流感人数是
多少?
(1)本题中的数量关系是什么?
分析:
……
被传染人
被传染人
……
被传染人
被传染人
……
……
x
x
开始传染源
1
被传染人
被传染人
x
设每轮传染中平均一个人传染了 x 个人,
开始传染源
被传染人
被传染人
……
x
第二轮的传染源有 人,有 人被传染.
1
x
x+1
2.解决“传播问题”
x x + 1
( )
传染源数、第一轮被传染数和第二轮被传染数的总和是 121 个人.
2.解决“传播问题”
探究 有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个
人?
(3)如何理解经过两轮传染后共有 121 个人患了
流感?
分析:
解:设每轮传染中平均一个人传染了 x 个人.
x1 =______,x2 =______
答:平均一个人传染了 10 个人.
10
(不合题意,舍去) .
-12
2.解决“传播问题”
探究 有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个
人?
(4)如何利用已知数量关系列出方程,并解方程
得出结论?
分析:
1 + x + x 1 + x = 121
( )
(5)如果按照这样的传染速度,三轮传染后有多
少个人患流感?
121+121×10 = 1 331(人)
(6)通过对这个问题的探究,你对类似的传播问
题中的数量关系有新的认识吗?
2.解决“传播问题”
3.巩固训练
某种植物的主干长出若干数目的支干,每个支干又
长出同样数目的小分支,主干,支干和小分支的总数是
91,每个支干长出多少个小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
解:设每个支干长
出 x 个小分支,则
1 + x + x·x = 91
x1 = 9,
x2 = -10(不合题意,舍去) .
答:每个支干长出 9 个小分支.
x
你能说说本节课所研究的“传播问题”的基本特征
吗?解决此类问题的关键步骤是什么?
“传播问题”的基本特征是:以相同速度逐轮传播.
解决此类问题的关键步骤是:明确每轮传播中的传
染源个数,以及这一轮被传染的总数.
4.归纳小结
┃ 实际问题与一元二次方程
变式训练
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过700台?
┃ 实际问题与一元二次方程
变式训练
解:设每轮感染中平均一台电脑会感染x台电脑.
依题意1+x+(1+x)x=81,
(1+x)2=81,x+1=9或x+1=-9.
解得x=8或x=-10(舍去)
三轮感染后被感染的电脑台数为
(1+x)2+(1+x)2x=(1+x)3=(1+8)3=729>700.
答:每轮感染中平均一台电脑会感染8台电脑;三轮感染后,被感染的电脑台数会超过700台.
小试牛刀
问题2:你能归纳一下上述两个问题中蕴含的共同等量关系吗?
=变化后的数量
变化前的数量
青山村种植水稻2020年平均每公顷产7200kg,2022年平均每公顷产8450kg, 求水稻每公顷产量的年平均增长率。(列出方程)
解:设水稻每公顷产量的年平均增长率为x
7200(1+x) kg
2022年平均每公顷产量为
7200(1+x)2 kg
2021年平均每公顷产量为
由此可列方程:
7200(1+x)2=8450
知识讲解
探究:两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大
药品 成本 甲 乙
两年前的成本
现在的成本
5000元
6000元
3000元
3600元
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率
1000元
1200元
?
?
知识讲解
本年成本=前一年成本-前一年成本×年下降率
=前一年成本×(1-年下降率)
知识讲解
难点突破
=变化后的数量
变化前的数量×(1-年下降率)2
连续两年下降:
知识讲解
难点突破
解:设甲种药品成本的年平均下降率为x
一年前甲种药品的成本为
5000-5000x=5000(1-x) 元,
现在甲种药品的成本为
=5000(1-x)2 元
5000(1-x)
(1-x)
知识讲解
难点突破
解:设甲种药品成本的年平均下降率为x
由题意得
5000(1-x)2=3000
解方程,得
(1-x)2=0.6
年平均下降率应为小于1的正数
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
知识讲解
难点突破
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率 22.5%.
1000元
1200元
?
解:设乙种药品成本的年平均下降率为y
由题意得 6000(1-y)2=3600
解方程,得
根据问题的实际意义
乙种药品成本的年平均下降率约为22.5%.
y1≈0.225,y2≈1.775
药品 成本 甲 乙
年平均下降额 1000元 1200元
年平均下降率 22.5%. 22.5%.
甲、乙两种药品成本的年平均下降率相等
由此可见成本下降额较大的产品,其成本
下降率不一定较大.
┃ 实际问题与一元二次方程
课堂训练
1. 生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,如果全组有x名同学,那么根据题意列出的方程是( )
A. x(x+1)=182 B. x(x-1)=182
C. 2x(x+1)=182 D. x(1-x)=182×2
B
课堂练习
难点巩固
2、某银行经过最近的两次降息,使一年期存款的年利率由2.25%降至1.98%,平均每次降息的百分率是多少?(精确到0.01%)?
3、向阳村2021年的人均收入为32000元,2022年的人均收入为34520元,求人均收入的年平均增长率.
6.19%
小结
1、你能概括一下“变化率问题”的基本特征吗?
2、解决“变化率问题”的关键步骤是什么?
“变化率问题”的基本特征:平均变化率保持不变;
变化前的数量
=变化后的数量
解决“变化率问题”的关键步骤:找出变化前的数量、变化后的数量,找出相应的等量关系.
┃ 实际问题与一元二次方程
课堂小结
1. 传播问题的要点:传染源与传播速度
2.若有a个人患流感,经过n轮传染后共有m人,设每个传染x人,则可列方程为:
3、你能概括一下“变化率问题”的基本特征吗?
4、解决“变化率问题”的关键步骤是什么?
“变化率问题”的基本特征:平均变化率保持不变;
变化前的数量
=变化后的数量
解决“变化率问题”的关键步骤:找出变化前的数量、变化后的数量,找出相应的等量关系.
21.3 实际问题与一元二次方程
1.分析“传播问题”的特征
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
2.解决“传播问题”
探究 有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个
人?
(2)每一轮的传染源和传染之后的患流感人数是
多少?
(1)本题中的数量关系是什么?
分析:
……
被传染人
被传染人
……
被传染人
被传染人
……
……
x
x
开始传染源
1
被传染人
被传染人
x
设每轮传染中平均一个人传染了 x 个人,
开始传染源
被传染人
被传染人
……
x
第二轮的传染源有 人,有 人被传染.
1
x
x+1
2.解决“传播问题”
x x + 1
( )
传染源数、第一轮被传染数和第二轮被传染数的总和是 121 个人.
2.解决“传播问题”
探究 有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个
人?
(3)如何理解经过两轮传染后共有 121 个人患了
流感?
分析:
解:设每轮传染中平均一个人传染了 x 个人.
x1 =______,x2 =______
答:平均一个人传染了 10 个人.
10
(不合题意,舍去) .
-12
2.解决“传播问题”
探究 有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个
人?
(4)如何利用已知数量关系列出方程,并解方程
得出结论?
分析:
1 + x + x 1 + x = 121
( )
(5)如果按照这样的传染速度,三轮传染后有多
少个人患流感?
121+121×10 = 1 331(人)
(6)通过对这个问题的探究,你对类似的传播问
题中的数量关系有新的认识吗?
2.解决“传播问题”
3.巩固训练
某种植物的主干长出若干数目的支干,每个支干又
长出同样数目的小分支,主干,支干和小分支的总数是
91,每个支干长出多少个小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
解:设每个支干长
出 x 个小分支,则
1 + x + x·x = 91
x1 = 9,
x2 = -10(不合题意,舍去) .
答:每个支干长出 9 个小分支.
x
你能说说本节课所研究的“传播问题”的基本特征
吗?解决此类问题的关键步骤是什么?
“传播问题”的基本特征是:以相同速度逐轮传播.
解决此类问题的关键步骤是:明确每轮传播中的传
染源个数,以及这一轮被传染的总数.
4.归纳小结
┃ 实际问题与一元二次方程
变式训练
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过700台?
┃ 实际问题与一元二次方程
变式训练
解:设每轮感染中平均一台电脑会感染x台电脑.
依题意1+x+(1+x)x=81,
(1+x)2=81,x+1=9或x+1=-9.
解得x=8或x=-10(舍去)
三轮感染后被感染的电脑台数为
(1+x)2+(1+x)2x=(1+x)3=(1+8)3=729>700.
答:每轮感染中平均一台电脑会感染8台电脑;三轮感染后,被感染的电脑台数会超过700台.
小试牛刀
问题2:你能归纳一下上述两个问题中蕴含的共同等量关系吗?
=变化后的数量
变化前的数量
青山村种植水稻2020年平均每公顷产7200kg,2022年平均每公顷产8450kg, 求水稻每公顷产量的年平均增长率。(列出方程)
解:设水稻每公顷产量的年平均增长率为x
7200(1+x) kg
2022年平均每公顷产量为
7200(1+x)2 kg
2021年平均每公顷产量为
由此可列方程:
7200(1+x)2=8450
知识讲解
探究:两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大
药品 成本 甲 乙
两年前的成本
现在的成本
5000元
6000元
3000元
3600元
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率
1000元
1200元
?
?
知识讲解
本年成本=前一年成本-前一年成本×年下降率
=前一年成本×(1-年下降率)
知识讲解
难点突破
=变化后的数量
变化前的数量×(1-年下降率)2
连续两年下降:
知识讲解
难点突破
解:设甲种药品成本的年平均下降率为x
一年前甲种药品的成本为
5000-5000x=5000(1-x) 元,
现在甲种药品的成本为
=5000(1-x)2 元
5000(1-x)
(1-x)
知识讲解
难点突破
解:设甲种药品成本的年平均下降率为x
由题意得
5000(1-x)2=3000
解方程,得
(1-x)2=0.6
年平均下降率应为小于1的正数
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
知识讲解
难点突破
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率 22.5%.
1000元
1200元
?
解:设乙种药品成本的年平均下降率为y
由题意得 6000(1-y)2=3600
解方程,得
根据问题的实际意义
乙种药品成本的年平均下降率约为22.5%.
y1≈0.225,y2≈1.775
药品 成本 甲 乙
年平均下降额 1000元 1200元
年平均下降率 22.5%. 22.5%.
甲、乙两种药品成本的年平均下降率相等
由此可见成本下降额较大的产品,其成本
下降率不一定较大.
┃ 实际问题与一元二次方程
课堂训练
1. 生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,如果全组有x名同学,那么根据题意列出的方程是( )
A. x(x+1)=182 B. x(x-1)=182
C. 2x(x+1)=182 D. x(1-x)=182×2
B
课堂练习
难点巩固
2、某银行经过最近的两次降息,使一年期存款的年利率由2.25%降至1.98%,平均每次降息的百分率是多少?(精确到0.01%)?
3、向阳村2021年的人均收入为32000元,2022年的人均收入为34520元,求人均收入的年平均增长率.
6.19%
小结
1、你能概括一下“变化率问题”的基本特征吗?
2、解决“变化率问题”的关键步骤是什么?
“变化率问题”的基本特征:平均变化率保持不变;
变化前的数量
=变化后的数量
解决“变化率问题”的关键步骤:找出变化前的数量、变化后的数量,找出相应的等量关系.
┃ 实际问题与一元二次方程
课堂小结
1. 传播问题的要点:传染源与传播速度
2.若有a个人患流感,经过n轮传染后共有m人,设每个传染x人,则可列方程为:
3、你能概括一下“变化率问题”的基本特征吗?
4、解决“变化率问题”的关键步骤是什么?
“变化率问题”的基本特征:平均变化率保持不变;
变化前的数量
=变化后的数量
解决“变化率问题”的关键步骤:找出变化前的数量、变化后的数量,找出相应的等量关系.
同课章节目录
