2022-2023学年人教版数学九年级上册22.3 实际问题与二次函数 课件(共20页)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册22.3 实际问题与二次函数 课件(共20页) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
22.3 实际问题与二次函数
x
y
O
x
y
O
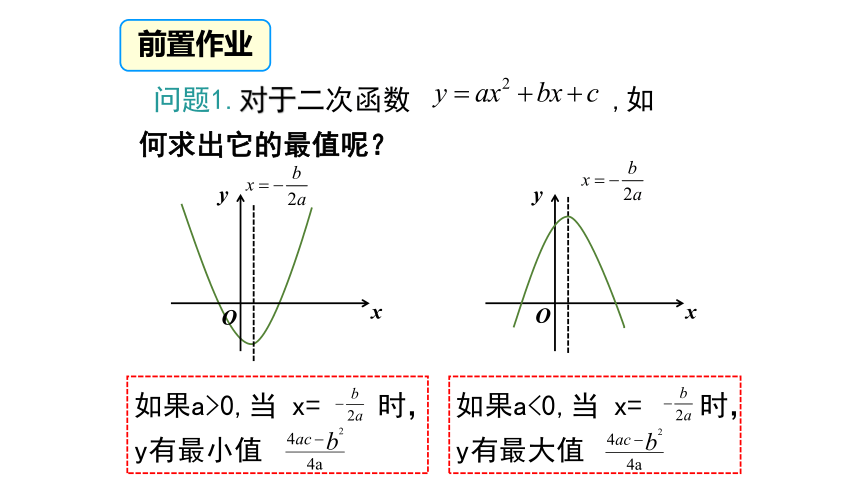
如果a>0,当 x= 时, y有最小值
如果a<0,当 x= 时,y有最大值
问题1.对于二次函数 ,如何求出它的最值呢?
前置作业
前置作业
问题2. 求出下列二次函数的最值。
(1)y=x2-4x-5 (2)y=-x2-3x+4
解:(1)顶点坐标:(2,-9)
即当x=2时,最小值:-9;
(2)顶点坐标:( , )
即 当 x= 时, 最大值: 。
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化。当l是多少时,场地的面积S最大?
合作探究
问题1:这个问题研究的是哪两个变量之间的关系
问题2:你能用学过的数学知识表示矩形的面积与一边长之间的数量关系吗
问题3:如何利用矩形的面积与边长之间的数量关系求出“当L是多少米时,场地的面积S最大”
探究:计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,如图,现有一张半径为45mm的磁盘.
(3)如果各磁道的存储单元数目与最内磁道相同.最内磁道的半径r是多少时,磁盘的存储量最大?
(1)磁盘最内磁道的半径为r mm,其上每0.015mm的弧长为1个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
y
0
x
5
10
15
20
25
30
1
2
3
4
5
7
8
9
1o
-1
6
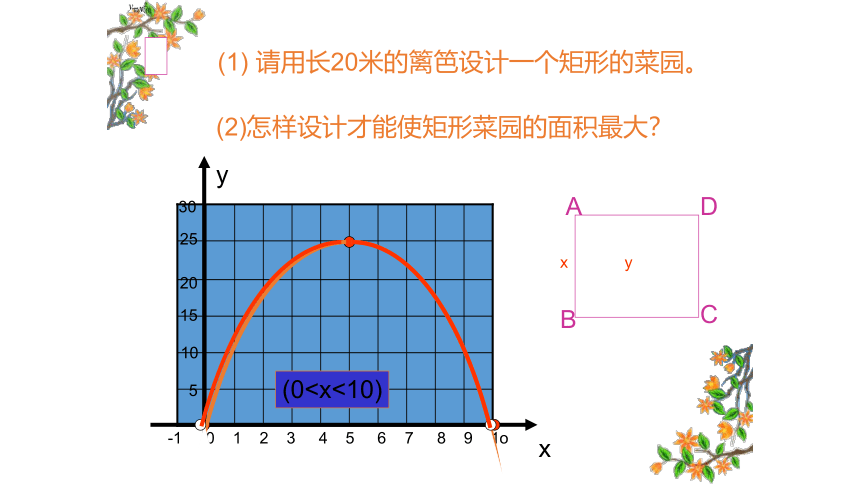
(1) 请用长20米的篱笆设计一个矩形的菜园。
(2)怎样设计才能使矩形菜园的面积最大?
A
B
C
D
x
y
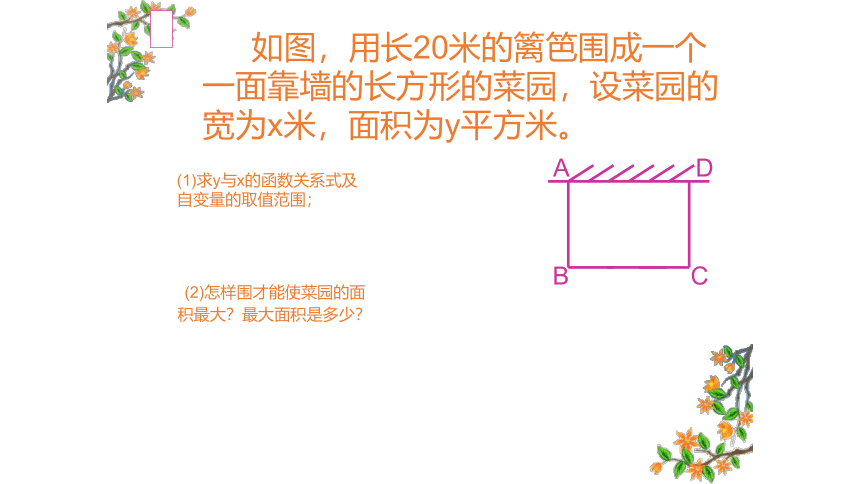
(0(1)求y与x的函数关系式及
自变量的取值范围;
(2)怎样围才能使菜园的面
积最大?最大面积是多少?
如图,用长20米的篱笆围成一个一面靠墙的长方形的菜园,设菜园的宽为x米,面积为y平方米。
A
B
C
D
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
解:
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)
=-4x2+24 x (0∴ 0<24-4x ≤6 4≤x<6
∴当x=4cm时,S最大值=32 平方米
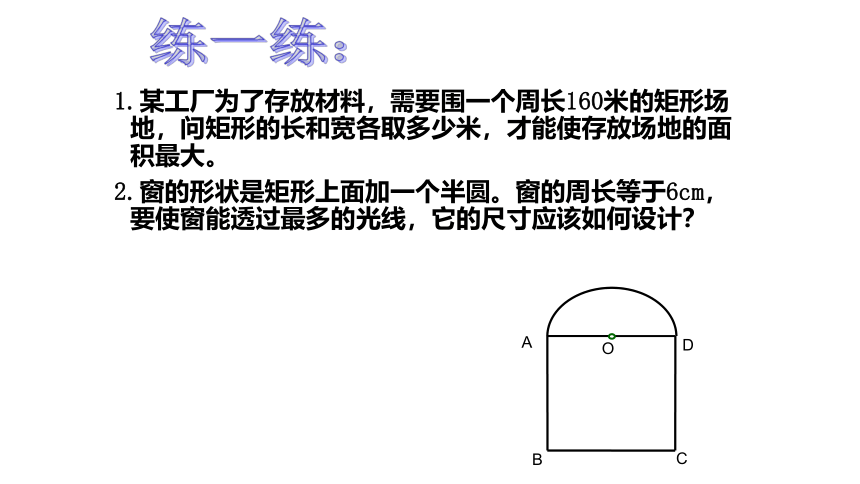
1.某工厂为了存放材料,需要围一个周长160米的矩形场地,问矩形的长和宽各取多少米,才能使存放场地的面积最大。
2.窗的形状是矩形上面加一个半圆。窗的周长等于6cm,要使窗能透过最多的光线,它的尺寸应该如何设计?
B
C
D
A
O
练一练:
3.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角120 的等腰梯形。要使水槽的横断面积最大,它的侧面AB应该是多长?
A
D
120
B
C
从形入手,探究问题
如图是抛物线形拱桥,当拱顶离水面 2 m,水
面宽 4 m. 水面下降 1 m,水面宽度增加多少?
小组合作,解决问题
如图是抛物线形拱桥,当拱顶离水面 2 m,水面宽 4 m. 水面下降 1 m,水面宽度增加多少?
小组合作:建立平面直角坐标系,运用所学知识,解决问题.
(每个小组建立2种不同的平面直角坐标系)
y=-0.5(x-2)2+2
y=-0.5x +2
y=-0.5x
y=-0.5(x+2)2+2
适当建系,优化解题
C
D
D
B
B
B
y=-0.5x +3
A
建立直角坐标系的基本原则:
(1)关注图形的对称性,以
对称轴为坐标轴;
(2)关注图形的特殊点,以
特殊点为坐标原点.
解:如图,以抛物线的顶点为原点,以抛物线的对称轴
为y轴建立平面直角坐标系.
设抛物线解析式为y=ax
∵抛物线经过点(2,-2),可得-2=a×2
∴a=-0.5 ,
∴这条抛物线为 y=-0.5x .
当水面下降1m时,水面的纵坐标为-3
这时有-3=-0.5x
解得: ,
此时水面宽度为 m
水面下降1m,水面宽度增加 m.
总结提升,提炼方法
某公园草坪的防护栏是由100段形状相同的抛物线形组成,为了牢固起见,每段护栏中需要间距4dm加设一根不锈钢的支柱,防护栏的最高点距底部5dm(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A、50m B、100m C、160m D、200m
巩固训练、拓展思维
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
请大家带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,销额为 元,买进商品需付 元因此,所得利润为 元
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
y=(60+x)(300-10x)-40(300-10x)
即
(0≤X≤30)
(0≤X≤30)
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值。由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。
解:设降价x元时利润最大,则每星期可多卖18x件,实际卖出(300+18x)件,销售额为(60-x)(300+18x)元,买进商品需付40(300-10x)元,因此,得利润
做一做
(0≤x≤20)
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。
解这类题目的一般步骤
22.3 实际问题与二次函数
x
y
O
x
y
O
如果a>0,当 x= 时, y有最小值
如果a<0,当 x= 时,y有最大值
问题1.对于二次函数 ,如何求出它的最值呢?
前置作业
前置作业
问题2. 求出下列二次函数的最值。
(1)y=x2-4x-5 (2)y=-x2-3x+4
解:(1)顶点坐标:(2,-9)
即当x=2时,最小值:-9;
(2)顶点坐标:( , )
即 当 x= 时, 最大值: 。
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化。当l是多少时,场地的面积S最大?
合作探究
问题1:这个问题研究的是哪两个变量之间的关系
问题2:你能用学过的数学知识表示矩形的面积与一边长之间的数量关系吗
问题3:如何利用矩形的面积与边长之间的数量关系求出“当L是多少米时,场地的面积S最大”
探究:计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,如图,现有一张半径为45mm的磁盘.
(3)如果各磁道的存储单元数目与最内磁道相同.最内磁道的半径r是多少时,磁盘的存储量最大?
(1)磁盘最内磁道的半径为r mm,其上每0.015mm的弧长为1个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
y
0
x
5
10
15
20
25
30
1
2
3
4
5
7
8
9
1o
-1
6
(1) 请用长20米的篱笆设计一个矩形的菜园。
(2)怎样设计才能使矩形菜园的面积最大?
A
B
C
D
x
y
(0
自变量的取值范围;
(2)怎样围才能使菜园的面
积最大?最大面积是多少?
如图,用长20米的篱笆围成一个一面靠墙的长方形的菜园,设菜园的宽为x米,面积为y平方米。
A
B
C
D
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
解:
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)
=-4x2+24 x (0
∴当x=4cm时,S最大值=32 平方米
1.某工厂为了存放材料,需要围一个周长160米的矩形场地,问矩形的长和宽各取多少米,才能使存放场地的面积最大。
2.窗的形状是矩形上面加一个半圆。窗的周长等于6cm,要使窗能透过最多的光线,它的尺寸应该如何设计?
B
C
D
A
O
练一练:
3.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角120 的等腰梯形。要使水槽的横断面积最大,它的侧面AB应该是多长?
A
D
120
B
C
从形入手,探究问题
如图是抛物线形拱桥,当拱顶离水面 2 m,水
面宽 4 m. 水面下降 1 m,水面宽度增加多少?
小组合作,解决问题
如图是抛物线形拱桥,当拱顶离水面 2 m,水面宽 4 m. 水面下降 1 m,水面宽度增加多少?
小组合作:建立平面直角坐标系,运用所学知识,解决问题.
(每个小组建立2种不同的平面直角坐标系)
y=-0.5(x-2)2+2
y=-0.5x +2
y=-0.5x
y=-0.5(x+2)2+2
适当建系,优化解题
C
D
D
B
B
B
y=-0.5x +3
A
建立直角坐标系的基本原则:
(1)关注图形的对称性,以
对称轴为坐标轴;
(2)关注图形的特殊点,以
特殊点为坐标原点.
解:如图,以抛物线的顶点为原点,以抛物线的对称轴
为y轴建立平面直角坐标系.
设抛物线解析式为y=ax
∵抛物线经过点(2,-2),可得-2=a×2
∴a=-0.5 ,
∴这条抛物线为 y=-0.5x .
当水面下降1m时,水面的纵坐标为-3
这时有-3=-0.5x
解得: ,
此时水面宽度为 m
水面下降1m,水面宽度增加 m.
总结提升,提炼方法
某公园草坪的防护栏是由100段形状相同的抛物线形组成,为了牢固起见,每段护栏中需要间距4dm加设一根不锈钢的支柱,防护栏的最高点距底部5dm(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A、50m B、100m C、160m D、200m
巩固训练、拓展思维
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
请大家带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,销额为 元,买进商品需付 元因此,所得利润为 元
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
y=(60+x)(300-10x)-40(300-10x)
即
(0≤X≤30)
(0≤X≤30)
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值。由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。
解:设降价x元时利润最大,则每星期可多卖18x件,实际卖出(300+18x)件,销售额为(60-x)(300+18x)元,买进商品需付40(300-10x)元,因此,得利润
做一做
(0≤x≤20)
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。
解这类题目的一般步骤
同课章节目录
