有理数的乘法[上学期]

(共16张PPT)
桌上放7只茶杯，杯口全部朝上，每次翻
转其中的4只，能否经过若干次翻转，把它们
翻成杯口全部朝下？
“±1”将告诉你：不管你翻转多少次，总
是无法使这7只杯口全部朝下．道理很简单，
用“+1”表示杯口朝上，“-1”表示杯口朝下，
问题就变成：“把7个+1每次改变其中4个的符号，若干次后能否都变成-1？”考虑这7个数的乘积，由于每次都改变4个数的符号，所以它们的乘积永远不变(为+1)。而7个杯口全部朝下时，7个数的乘积等于-1，这是不可能的。
解：5×3 = 15
计算:
(1) 5 × 3
(2) ×
(3)0 ×
2
3
7
4
1
4
解： × =
2
3
7
4
7
6
解：0 × = 0
1
4
（1）（+2）×（+3）
（+2）：看作向东运动2米；
×（+3）：看作沿原方向运动3次
2
0
2
6
4
结果：向东运动6米。（+2）×（+3）= +6
6
-6
-4
0
-2
2
-6
(2) （-2）×（+3）
（-2）：看作向西运动2米；
×（+3）：看作沿原方向运动3次;
结果：向西运动6米。（-2）×（+3）＝-6
-6
(3) （+2）×（-3）
（+2）：看作向东运动2米；
×（-3）：看作沿反方向运动3次。
结果：向西运动6米。（+2）×（-3）= - 6
2
-6
-4
0
-2
2
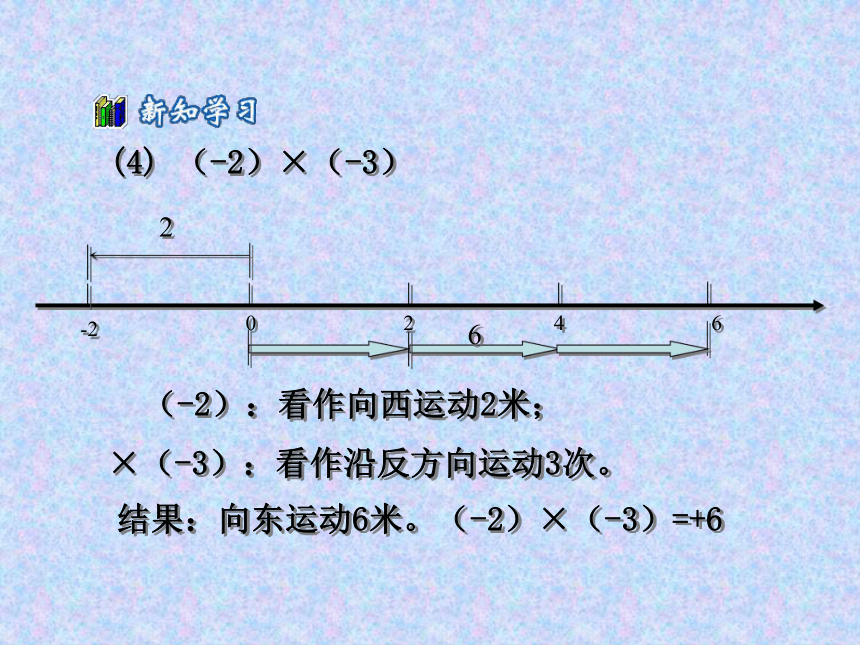
(4) （-2）×（-3）
（-2）：看作向西运动2米；
×（-3）：看作沿反方向运动3次。
结果：向东运动6米。（-2）×（-3）=+6
2
6
0
2
6
4
-2
（5） 0 × 5 = 0
在原地运动5次
（-5）× 0 = 0
向西方运动0次
结果：被乘数是0或者乘数是0，结果仍在原处。
0 × 0 = 0
（1）2×3=6 （2）（-2）×3= -6
（3）2×（-3）= -6
（4）（-2）×（-3）=6
（5） 被乘数或乘数为0时，结果是0
有理数乘法法则：两数相乘，同号得正， 异号得负，并把绝对值相乘。任何数 同0相乘，都得0。
5个例子综合如下：
练习1：确定下列积的符号：
（１） 5×（-3）　
（２）（-4）×6
（３）（-7）×（-9）
（４） 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
例如 （-7） ×（- 4）
（同号两数乘）
（-7）×（- 4）= +（ ）
（得正）
7×4 = 28
（把绝对值相乘）
∴（-7）×（-4）= 28
又如：（-7）×4
（异号两数相乘）
（-7）×4 = -（　）
（得负）
7×4 = 28
（把绝对值相乘）
∴（-7）×4 = -28
注意:一个数同+1相乘，得原数，
一个数同-1相乘，得原数的相反数。
例1 计算:
(1) (-3)×(-9) (2) (- ) ×
(3) 7 ×(-1) (4) (-0.8) ×1
1
2
1
3
解: (1) (-3) ×(-9) = 27
(2) ( - ) × = -
(3) 7 ×(-1) = -7
(4) (-0.8) ×1 = -0.8
1
2
1
3
1
6
计算（口答）：
（1） 6×（-9）＝
（2）（-6）×（-9）＝
（3）（-6）×9 ＝
（4） (-6）×1＝
（5） ( -6）×（-1） ＝
（6） 6×（-1） ＝
填空:
1×(-5)=___ (-1)×(-5)=___
(2)1× a =___ (-1)× a =___
-5
5
a
-a
-５４
５４
-５４
-６
６
-６
用“＜”或“＞”号填空:
(1)如果a＜0 b＞0那么 ab___0
(2)如果a＜0 b＜0那么 ab___0
计算:
(1) (-6)×0.25 (2) (0.5)×(-8)
(3) - × (4) 2.9×(-0.4)
4
9
2
3
=-1.5
=-4
=-
8
27
=-1.16
＞
<
判断下列方程的解是正数、负数还是0：
（1） 4X= -16 （2）-3X=18
（3）-9X=-36 （4）-5X=0
思考题
（1）当a＞0时，a与2a哪个大？
（2）当a＜0时，a与2a那个大？
正数
负数
0
负数
2a大
a大
小结：
1.有理数乘法法则：
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.如何进行两个有理数的运算：
先确定积的符号，再把绝对值相乘，当有一个因数为零时，积为零。