列代数式[上学期]

课件29张PPT。列 代 数 式如果长方形的长是x米，那么所得结果就会是一个含有x的式子。
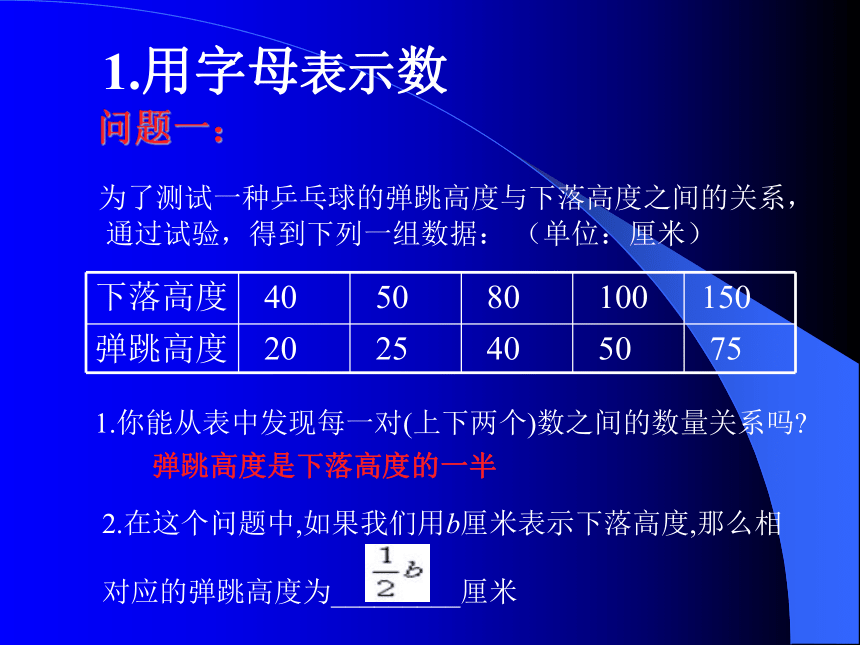
我们如果将这类式子变形和化简，就会涉及到代数式整式的有关知识了。本章我们将学习代数式，特别是整式及其加减法。§3.1 列代数式第一课时问题一： 为了测试一种乒乓球的弹跳高度与下落高度之间的关系，通过试验，得到下列一组数据： （单位：厘米）
1.你能从表中发现每一对(上下两个)数之间的数量关系吗?弹跳高度是下落高度的一半2.在这个问题中,如果我们用b厘米表示下落高度,那么相
对应的弹跳高度为_________厘米1.用字母表示数用字母b表示下落高度以后，得出表示弹跳高度的一个式子b/2反映了皮球弹跳高度和下落高度之间的数量关系。
根据这个关系式，可以由任意给的皮球的高度，求得相应的弹跳高度。例如，如果下落高度为200米，那么弹跳高度是多少呢？
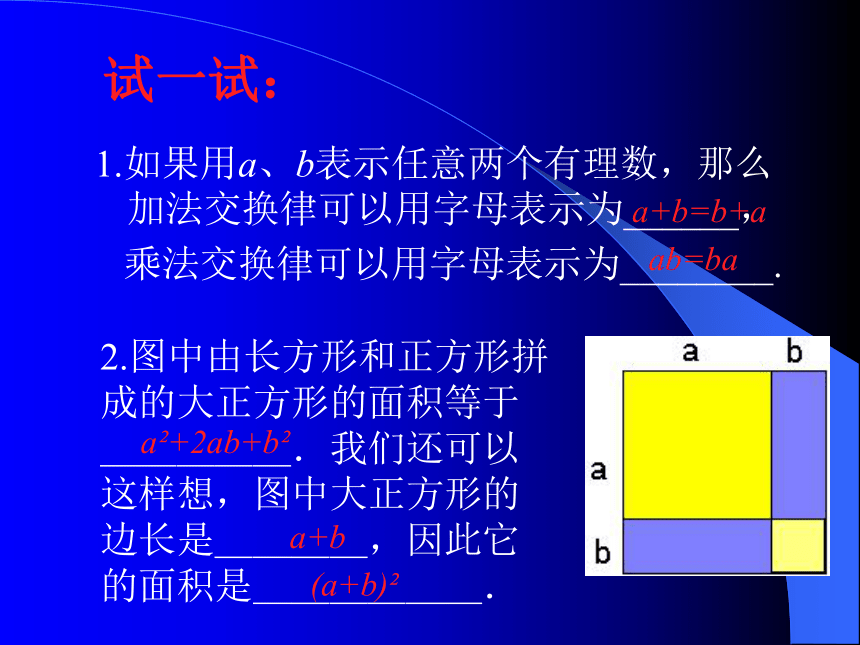
1.如果用a、b表示任意两个有理数，那么加法交换律可以用字母表示为______，
乘法交换律可以用字母表示为________.试一试：a+b=b+aab=ba2.图中由长方形和正方形拼　成的大正方形的面积等于　＿＿＿＿＿．我们还可以　这样想，图中大正方形的　边长是＿＿＿＿，因此它　的面积是＿＿＿＿＿＿．a2+2ab+b2a+b(a+b)2
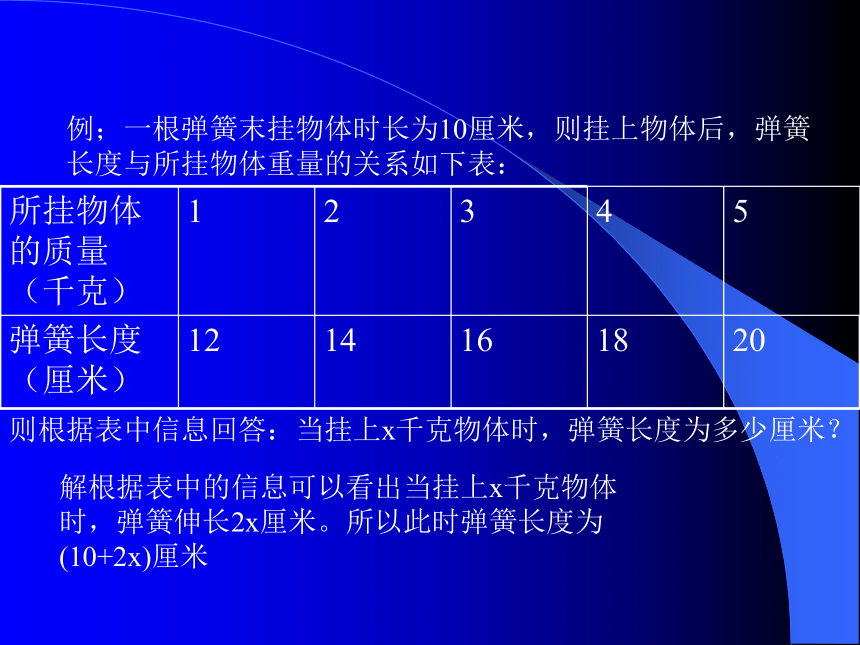
例；一根弹簧末挂物体时长为10厘米，则挂上物体后，弹簧长度与所挂物体重量的关系如下表：则根据表中信息回答：当挂上x千克物体时，弹簧长度为多少厘米？解根据表中的信息可以看出当挂上x千克物体时，弹簧伸长2x厘米。所以此时弹簧长度为(10+2x)厘米注意：

（1）在用字母表示数时，字母与字母之间的 乘号，一般省略不写，或者乘号用“?” 表示。如第一题中的a×b一般写为ab或a?b。
（2）数字与字母相乘，数字一般放在字母的前面,带分数需化假分数。
（3）上面运算律中，所用到的字母a、b都是表的字母，它代表我们过去学过的一切数。
（4)两数相除，除号用分数线代替
问题二：你能用下面的图来
解释左边３个等式吗？１＋２＋３＋４＋５＝＿＿＿＿＿＝＿＿
……
１＋２＋３＋…＋１００＝＿＿＿＿＿＿＝＿＿＿＿
１＋２＋３＋…＋n＝＿＿＿＿＿＿１５５０５０由以上规律进一步填空如图所示的窗框，上半部为半圆，下半部为长方形，长方形的长为a与宽为b,则它的透光面积是 平方米，这个窗框需要材料— — 米。例：
小 结：从上面的例子看到，用字母表示数，可以更一般地研究数量关系，为我们解决问题带来方便．用字母表示数是代数的一个重要特点，小学里已接触过用字母表示数，初中将进一步研究用字母表示数．练一练：１.某地为了治理河山，改造环境，计划在第十个五年计划期间绿化荒山，如果每年植物绿化x公顷荒山，那么这五年内植树绿化荒山＿＿＿公顷．
２.如果小红用t小时走完的路程为s千米，那么她的速度为＿＿＿＿＿千米／小时．
３.每本练习本m元，甲买了５本，乙买了２本，两个人一共花了＿＿＿＿＿＿＿元，甲比乙多花了＿＿＿＿＿元．５xs/t(5m+2m)(5m–2m)1)温度由t上升3后是_____________
2)一个两位数，个位数字是a，十位数字是b，则这个两位数是______________
3）一个三位数，个位数字是a，十位数字是a+1,百位数字是a+2，则这个三位数是__________
4）连续三个自然数，中间一个为n，则它的前面一个是________，这三个自然数的和是______
5)小亮今年13岁，小明比小亮大x岁。十年后，
小明的年龄是____ 岁，比小亮大____岁t+310b+a100(a+2)+10(a+1)+an-13n23+xx小结：本节课我们所学的内容是什么？
2. 用代数式表示应注意什么？
做一做：填空：
（1）某种瓜子的单价为16元/千克，则n千克需要 _____元。
（2）小刚上学步行速度为5千米/小时
若小刚到学校的路程为s千米，则他上学需走________小时。
（3）钢笔每枝a元，铅笔每枝b元，买2支钢笔和3支铅笔共需__________元。16ns/5（2a+3b）概括：上面的这些问题中出现的如16n，s/5，2a+3b，以及上节课出现的 a，b，a+b，a?b，a2，（a+b）2，15，5050， ，5x，s/t等式子，我们称它为代数式。即代数式是用运算符号把数和表示数的字母连接而成的式子问题： 单独的一个数或一个字母也是代数式吗？我们的答案是肯定的。即:单独的一个数或一个字母也是代数式。例判断下列哪些是代数式哪些不是代数式？
5，a, 3-a, ,5X2+Y2例1：填空：（1）圆的半径为r cm，它的面积为______cm2.
（2）长方形的长与宽分别为a cm、b cm，则该长方形的周长__________cm.
（3）小强在小学六年中共攒了a元零花钱，上中学后买文具用去b元，剩下的钱全部存入银行，则小强可以存款___________元。
（4）某机关原有工作人员 m 人，现精简机构，减少20%的工作人员，则有________人被精简。?r22(a+b） （a–b）20%·m例填空：
1）乒乓球比赛分成m组，每组4人，则参加比赛的共 ------------人
2）某校男生人数是全校的46，而女生人数为x人，则全校学生人数为————
3）甲已两人分别从相距s千米的两地同时出发，相向而行，甲的速度为x千米/小时，则甲已两人经过——小时相遇例2. 结合你的生活经验对下列代数式作出具体解释：
（1）a–b; (2) ab解：（1）今年小明b岁、小明爸爸a岁，小明比他爸爸小（a–b）岁； （2）长方形的长为a厘米，宽为b厘米，长方形的面积是ab平方厘米。说出下列代数式的意义：
1）（a+b)(a－b) 2) a－b2
3) x3＋y3 4) (x2 －y2)1)a、b的和与a、b的差的积2)a与b的平方之差3)x与y的立方和4)x与y的平方差的二分之一试问：照上图搭下去
（1）第5个图形需要多少根火柴？（2）第n个图形需要多少根火柴？做一做：下列代数式哪些书写不规范，请改正过来
3x+1 2. m?n–3 3. 2?y
4. 5. a?(b+c) 6. a–1?b复习提问：1. 书写代数式要注意什么？答： 书写代数式要注意三点（1）代数式中出现乘号，通常写作“?”或省略不写；（2）数字与字母相乘，数字写在字母前面；（3）除法运算写成分数形式。2. 填空
（1）长为a米，宽为b米的长方形的周长是__________米。
（2） 半径为r厘米的圆面积增加了10%，增加面积_________平方厘米2（a+b）10%·r做一做： 请同学们思考以下问题并填空：
某地区夏季高山上的温度从山脚处开始每升高100米降低0.7oC。如果山脚温度是28oC，那么山上300米处的温度为________一般地，山上x米处的温度
为_____________.25.9oCoC要解决以上问题的，需要学习列代数式。在解决一些实际问题时，往往先把问题中与数量有关的词语用代数式表示出来，使问题变得更简洁，更具一般性。例1：设某数为x，用代数式表示：
（1） 比某数的 大1的数；
（2） 比某数大10%的数；
（3） 某数与 的和的三倍；
（4） 某数的倒数与5的差.解：（1）（2）（1+10%）x（3） （4）例2.用代数式表示 （1） a、b两数的平方和减去他们乘积的2倍；
（2） a、b两数的和的平方减去他们的差的平方；
（3） a、b两数的和与他们的差的乘积；
（4） 偶数、奇数.（三个连续偶数，三个连续偶数解：（1） a2 +b2–2ab （2）( a+b)2 –(a–b)2（3）(a+b)(a–b)（4）2n，2n+1(n为整数)(5）个位数为X，十位数为Y，百位数字为Z 的三位数。（5）100Z+10Y+X