湘教版数学九年级下册 1.2 二次函数y=ax2+bx+c的图象与性质( 第5课时) 课件(共19张PPT)
文档属性
| 名称 | 湘教版数学九年级下册 1.2 二次函数y=ax2+bx+c的图象与性质( 第5课时) 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 939.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 07:04:51 | ||
图片预览






文档简介
(共19张PPT)
第1章 二次函数
1.2 第5课时 二次函数y=ax2+bx+c 的图象与性质
如何画二次函数 的图象
新课导入
我们会画 的图象。把 配方成 的形式即可.
配方:
获取新知
你能描述配方
的步骤吗?
如何把 配方成 的形式
对于一般的二次函数,又该如何配方呢?
配方:
一般地,二次函数y=ax2+bx+c的可以通过配方化成y=a(x-h)2+k的形式,即
归纳总结
如何画二次函数 的图象?
由上述知识可知把 转化成
接下来画 的图像即可.
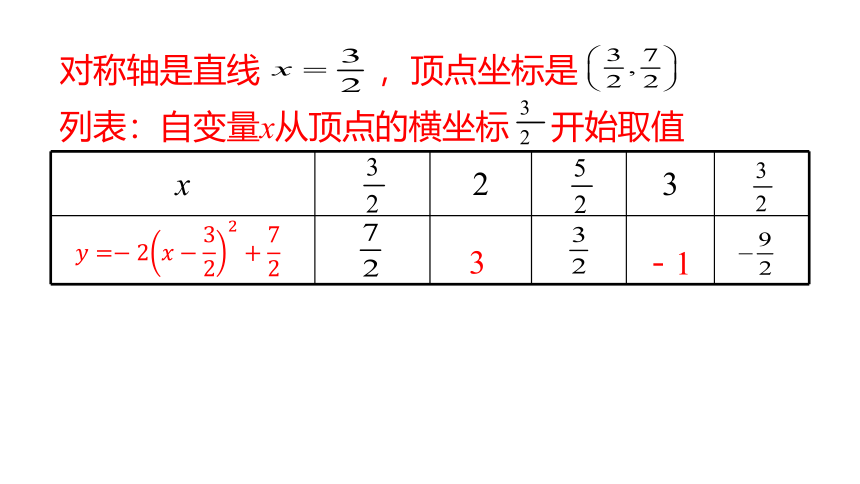
对称轴是直线 ,顶点坐标是
列表:自变量x从顶点的横坐标 开始取值
x 2 3
3
-1
x
y
o
1
2
3
4
-1
-2
-3
-4
3
2
4
1
-5
-1
描点和连线:画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分,这样就得到函数 的图象,如图
从图看出,当x等于多少时,函数 的值最大?这个最大值是多少?
当x等于顶点的横坐标 时,函数值( ),这个最大值等于顶点的纵坐标 。
说一说
x
y
o
1
2
3
4
-1
-2
-3
-4
3
2
4
1
-5
-1
最大
再观察二次函数 的图像,当x等于多少时,函数值最小?这个最小值等于多少?
O
y
2
4
-2
-4
2
4
-2
-4
x
一般地,有下述结论:
二次函数 当x等于顶点的横坐标时,达到最大值(当a<0)或最小值(当a>0),这个最大(小)值等于顶点的纵坐标.
归纳总结
练一练
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,3)
直线x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,-6)
直线x=
填表:
例1 求函数 的最大值
解:配方得
顶点坐标是(2,1),
于是当x=2时,y达到最大值1.
例题讲解
一般地,对于二次函数
配方:
顶点坐标是
因此,当 时,
函数达到最大值(当a<0)
或最小值(当a>0):
归纳总结
1.抛物线y=x2-2x+3的二次项系数a=____,一次项系数b=____,常数项c=____,所 以-=____, =____,其 顶 点 式 为 y=___________,顶点坐标是________.
1
-2
3
1
2
(x-1)2+2
(1,2)
随堂演练
2.下图是二次函数y=ax2+bx+c图象的一部分,由图知抛物线的对称轴是直线x=____,根据对称性可知该图在y轴右侧与x轴交点的坐标是______.
-1
(1,0)
3.函数y=x2+4x+3,当x_______时,y的值随着x的值的增大而增大;当x_______时,y的值随着x的值的增大而减小.
4.二次函数y=ax2-2x+1的图象经过点(1,2),则其图象开口_______.
>-2
<-2
向上
5.已知二次函数 y=3x2-6x-24.
(1)通过配方,写出该二次函数图象的开口方向、对称轴和顶点坐标;
(2)利用对称性画出这个二次函数的图象.
解: (1)y=3x2-6x-24
=3(x2-2x+1)-24-3
=3(x-1)2-27.
∵a=3>0,
∴抛物线开口向上,对称轴为直线x=1,
顶点坐标为(1,-27).
(2)略.
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
最值:
课堂小结
第1章 二次函数
1.2 第5课时 二次函数y=ax2+bx+c 的图象与性质
如何画二次函数 的图象
新课导入
我们会画 的图象。把 配方成 的形式即可.
配方:
获取新知
你能描述配方
的步骤吗?
如何把 配方成 的形式
对于一般的二次函数,又该如何配方呢?
配方:
一般地,二次函数y=ax2+bx+c的可以通过配方化成y=a(x-h)2+k的形式,即
归纳总结
如何画二次函数 的图象?
由上述知识可知把 转化成
接下来画 的图像即可.
对称轴是直线 ,顶点坐标是
列表:自变量x从顶点的横坐标 开始取值
x 2 3
3
-1
x
y
o
1
2
3
4
-1
-2
-3
-4
3
2
4
1
-5
-1
描点和连线:画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分,这样就得到函数 的图象,如图
从图看出,当x等于多少时,函数 的值最大?这个最大值是多少?
当x等于顶点的横坐标 时,函数值( ),这个最大值等于顶点的纵坐标 。
说一说
x
y
o
1
2
3
4
-1
-2
-3
-4
3
2
4
1
-5
-1
最大
再观察二次函数 的图像,当x等于多少时,函数值最小?这个最小值等于多少?
O
y
2
4
-2
-4
2
4
-2
-4
x
一般地,有下述结论:
二次函数 当x等于顶点的横坐标时,达到最大值(当a<0)或最小值(当a>0),这个最大(小)值等于顶点的纵坐标.
归纳总结
练一练
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,3)
直线x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,-6)
直线x=
填表:
例1 求函数 的最大值
解:配方得
顶点坐标是(2,1),
于是当x=2时,y达到最大值1.
例题讲解
一般地,对于二次函数
配方:
顶点坐标是
因此,当 时,
函数达到最大值(当a<0)
或最小值(当a>0):
归纳总结
1.抛物线y=x2-2x+3的二次项系数a=____,一次项系数b=____,常数项c=____,所 以-=____, =____,其 顶 点 式 为 y=___________,顶点坐标是________.
1
-2
3
1
2
(x-1)2+2
(1,2)
随堂演练
2.下图是二次函数y=ax2+bx+c图象的一部分,由图知抛物线的对称轴是直线x=____,根据对称性可知该图在y轴右侧与x轴交点的坐标是______.
-1
(1,0)
3.函数y=x2+4x+3,当x_______时,y的值随着x的值的增大而增大;当x_______时,y的值随着x的值的增大而减小.
4.二次函数y=ax2-2x+1的图象经过点(1,2),则其图象开口_______.
>-2
<-2
向上
5.已知二次函数 y=3x2-6x-24.
(1)通过配方,写出该二次函数图象的开口方向、对称轴和顶点坐标;
(2)利用对称性画出这个二次函数的图象.
解: (1)y=3x2-6x-24
=3(x2-2x+1)-24-3
=3(x-1)2-27.
∵a=3>0,
∴抛物线开口向上,对称轴为直线x=1,
顶点坐标为(1,-27).
(2)略.
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
最值:
课堂小结
