湘教版数学九年级下册2.2.1 圆心角 课件(共15张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.2.1 圆心角 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 454.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 17:52:42 | ||
图片预览




文档简介
(共15张PPT)
第二章 圆
2.2.1 圆心角
1.圆是轴对称图形吗?它的对称轴是?
圆是轴对称图形,对称轴是直径所在的直线
2.绕圆心转动一个圆,它会发生什么变化吗?圆是中心对称图形吗?它的对称中心在哪里?
它是不会发生变化的,我们称之为“圆具有旋转不变性”.圆是中心对称图形,它的对称中心是圆心.
今天这节课我们将运用圆的旋转不变性
去探究弧、弦、圆心角的关系定理.
知识回顾
飞镖靶、闹钟以及被均分的蛋糕等圆形中,都存在着角,那么这些角有什么共同的特征呢?
获取新知
圆心角:顶点在圆心,角的两边与圆相交的角叫作圆心角.
·
O
B
A
如∠AOB(或∠BOA),我们把它叫做 所对的圆心角。
也可以叫做弦AB所对的圆心角∠AOB。
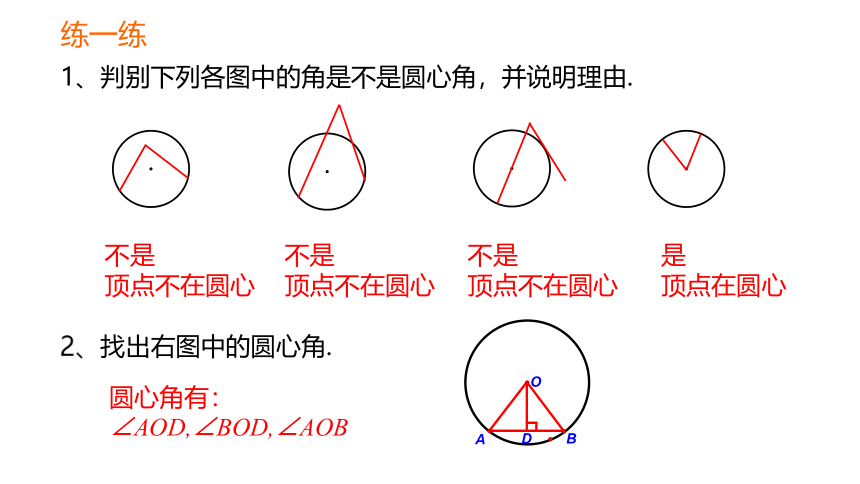
1、判别下列各图中的角是不是圆心角,并说明理由.
不是
顶点不在圆心
不是
顶点不在圆心
不是
顶点不在圆心
是
顶点在圆心
2、找出右图中的圆心角.
圆心角有:∠AOD,∠BOD,∠AOB
练一练
·
O
C
B
A
D
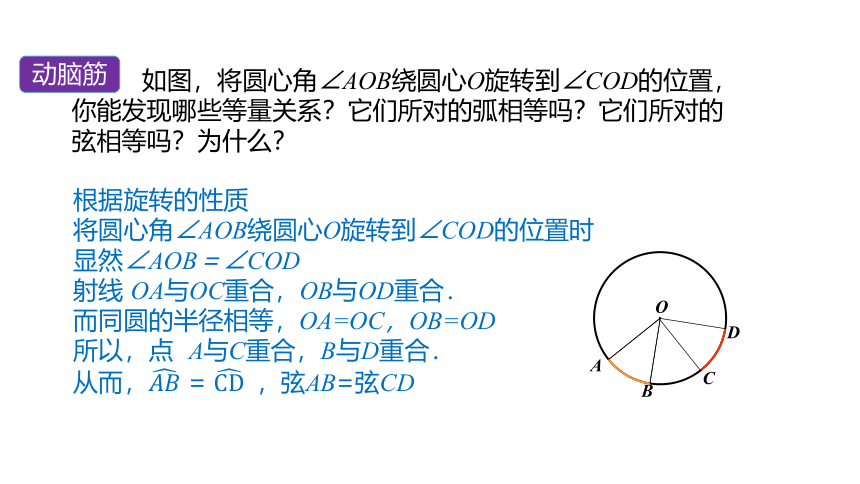
如图,将圆心角∠AOB绕圆心O旋转到∠COD的位置,你能发现哪些等量关系?它们所对的弧相等吗?它们所对的弦相等吗?为什么?
根据旋转的性质
将圆心角∠AOB绕圆心O旋转到∠COD的位置时
显然∠AOB=∠COD
射线 OA与OC重合,OB与OD重合.
而同圆的半径相等,OA=OC,OB=OD
所以,点 A与C重合,B与D重合.
从而, = , 弦AB=弦CD
动脑筋
O
·
A
B
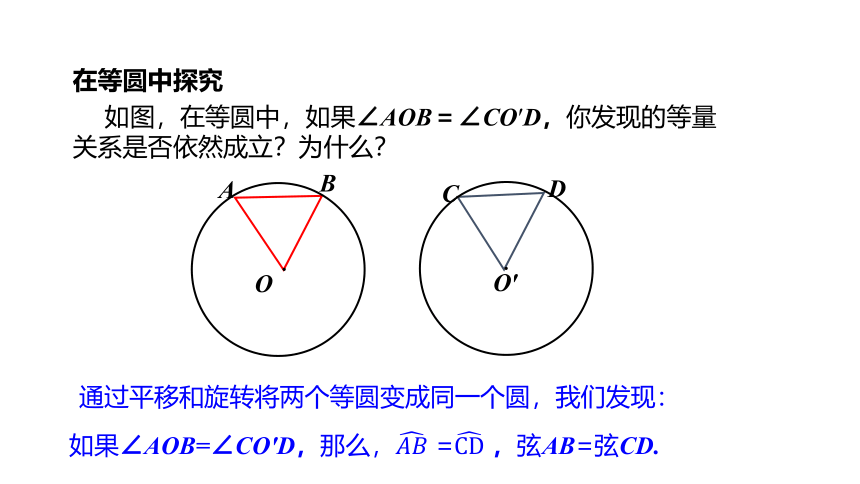
如图,在等圆中,如果∠AOB=∠CO′D,你发现的等量关系是否依然成立?为什么?
·
O′
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO'D,那么, = ,弦AB=弦CD.
在同圆或等圆中,相等的弧所对的
圆心角_____,所对的弦______;
在同圆或等圆中,相等的弦所对的
圆心角_____,所对的优弧______.
弧、弦与圆心角的关系定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
前提:一定是在同圆或等圆中
对象:圆心角,弦,弧
关系:知一推二
注意:弧有优劣之分,一弦对二弧
例1. 如图,AD=BC, 比较与的长度,并证明你的结论.
例题讲解
证明:∵AD=BC
∴ += +
∴ =
即
=
=
结论:
例2 如图,等边△ABC的顶点A,B,C在⊙O上,求圆心角∠AOB的度数 .
·
A
B
C
O
∴ AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
解:∵△ABC是等边三角形 ,
又∵ ∠AOB+∠BOC+∠AOC=360°.
∴ ∠AOB= (∠AOB+∠BOC+∠AOC)
= 360°=120°.
随堂演练
1.下列四个图中的角,是圆心角的是( )
B
2.在同圆或等圆中,下列说法错误的是( )
A.相等的弦所对的弧相等
B.相等的弦所对的圆心角相等
C.相等的圆心角所对的弧相等
D.相等的圆心角所对的弦相等
A
3. 已知⊙O的半径为5 cm,弦AB的长为5 cm,则弦AB所对的圆心角∠AOB=______.
60°
弦长等于半径的弦所对的圆心角等于60°.
AB=CD
⌒ ⌒
∠AOB=∠COD
AB=CD,
(1)∵∠AOB=∠COD,∴_________,________.
(2)∵AB=CD,∴_______________,__________.
(3)∵AB=CD,∴_______________,________.
4.如图,AB,CD是⊙O的两条弦.
⌒ ⌒
AB=CD
⌒ ⌒
AB=CD
∠AOB=∠COD
5. 如图,AB是⊙O 的直径,= = ,∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
∵
∴∠BOC=∠DOE=∠COD=35°
∴∠AOE=180°-3×35°
=75°
课堂小结
圆心角
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
前提条件:在同圆或等圆中
概念:顶点在圆心的角
第二章 圆
2.2.1 圆心角
1.圆是轴对称图形吗?它的对称轴是?
圆是轴对称图形,对称轴是直径所在的直线
2.绕圆心转动一个圆,它会发生什么变化吗?圆是中心对称图形吗?它的对称中心在哪里?
它是不会发生变化的,我们称之为“圆具有旋转不变性”.圆是中心对称图形,它的对称中心是圆心.
今天这节课我们将运用圆的旋转不变性
去探究弧、弦、圆心角的关系定理.
知识回顾
飞镖靶、闹钟以及被均分的蛋糕等圆形中,都存在着角,那么这些角有什么共同的特征呢?
获取新知
圆心角:顶点在圆心,角的两边与圆相交的角叫作圆心角.
·
O
B
A
如∠AOB(或∠BOA),我们把它叫做 所对的圆心角。
也可以叫做弦AB所对的圆心角∠AOB。
1、判别下列各图中的角是不是圆心角,并说明理由.
不是
顶点不在圆心
不是
顶点不在圆心
不是
顶点不在圆心
是
顶点在圆心
2、找出右图中的圆心角.
圆心角有:∠AOD,∠BOD,∠AOB
练一练
·
O
C
B
A
D
如图,将圆心角∠AOB绕圆心O旋转到∠COD的位置,你能发现哪些等量关系?它们所对的弧相等吗?它们所对的弦相等吗?为什么?
根据旋转的性质
将圆心角∠AOB绕圆心O旋转到∠COD的位置时
显然∠AOB=∠COD
射线 OA与OC重合,OB与OD重合.
而同圆的半径相等,OA=OC,OB=OD
所以,点 A与C重合,B与D重合.
从而, = , 弦AB=弦CD
动脑筋
O
·
A
B
如图,在等圆中,如果∠AOB=∠CO′D,你发现的等量关系是否依然成立?为什么?
·
O′
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO'D,那么, = ,弦AB=弦CD.
在同圆或等圆中,相等的弧所对的
圆心角_____,所对的弦______;
在同圆或等圆中,相等的弦所对的
圆心角_____,所对的优弧______.
弧、弦与圆心角的关系定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
前提:一定是在同圆或等圆中
对象:圆心角,弦,弧
关系:知一推二
注意:弧有优劣之分,一弦对二弧
例1. 如图,AD=BC, 比较与的长度,并证明你的结论.
例题讲解
证明:∵AD=BC
∴ += +
∴ =
即
=
=
结论:
例2 如图,等边△ABC的顶点A,B,C在⊙O上,求圆心角∠AOB的度数 .
·
A
B
C
O
∴ AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
解:∵△ABC是等边三角形 ,
又∵ ∠AOB+∠BOC+∠AOC=360°.
∴ ∠AOB= (∠AOB+∠BOC+∠AOC)
= 360°=120°.
随堂演练
1.下列四个图中的角,是圆心角的是( )
B
2.在同圆或等圆中,下列说法错误的是( )
A.相等的弦所对的弧相等
B.相等的弦所对的圆心角相等
C.相等的圆心角所对的弧相等
D.相等的圆心角所对的弦相等
A
3. 已知⊙O的半径为5 cm,弦AB的长为5 cm,则弦AB所对的圆心角∠AOB=______.
60°
弦长等于半径的弦所对的圆心角等于60°.
AB=CD
⌒ ⌒
∠AOB=∠COD
AB=CD,
(1)∵∠AOB=∠COD,∴_________,________.
(2)∵AB=CD,∴_______________,__________.
(3)∵AB=CD,∴_______________,________.
4.如图,AB,CD是⊙O的两条弦.
⌒ ⌒
AB=CD
⌒ ⌒
AB=CD
∠AOB=∠COD
5. 如图,AB是⊙O 的直径,= = ,∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
∵
∴∠BOC=∠DOE=∠COD=35°
∴∠AOE=180°-3×35°
=75°
课堂小结
圆心角
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
前提条件:在同圆或等圆中
概念:顶点在圆心的角
