湘教版数学九年级下册2.3 垂径定理 课件(共16张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.3 垂径定理 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 356.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 22:18:50 | ||
图片预览



文档简介
(共16张PPT)
第2章 圆
2.3 垂径定理
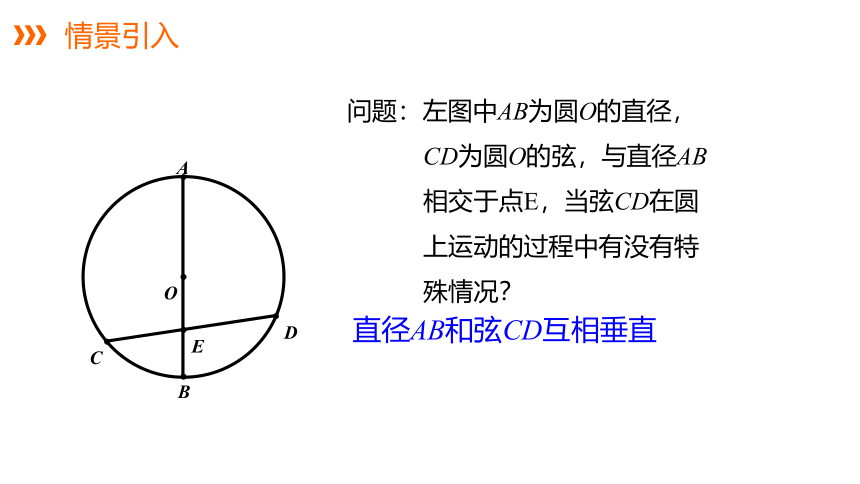
问题:左图中AB为圆O的直径,CD为圆O的弦,与直径AB相交于点E,当弦CD在圆上运动的过程中有没有特殊情况?
直径AB和弦CD互相垂直
情景引入
E
A
O
D
B
C
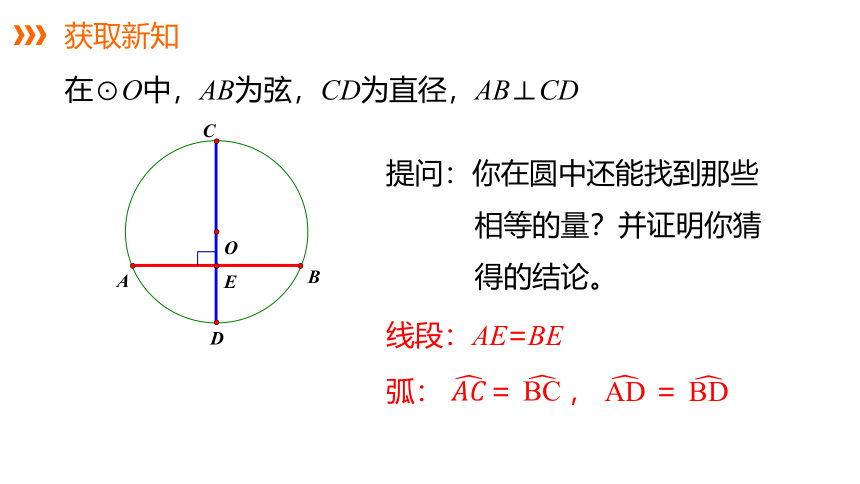
在⊙O中,AB为弦,CD为直径,AB⊥CD
提问:你在圆中还能找到那些相等的量?并证明你猜得的结论。
线段:AE=BE
弧: = , =
获取新知
E
D
C
O
A
B
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE,= , = 。
证明:连结OA、OB,则OA=OB.
∴△OAB是等腰三角形.
∵OE⊥AB,
∴AE=BE,∠AOE=∠BOE ,
∴∠AOC=∠BOC ,
∴ = , = .
C
.
O
A
E
B
D
┗
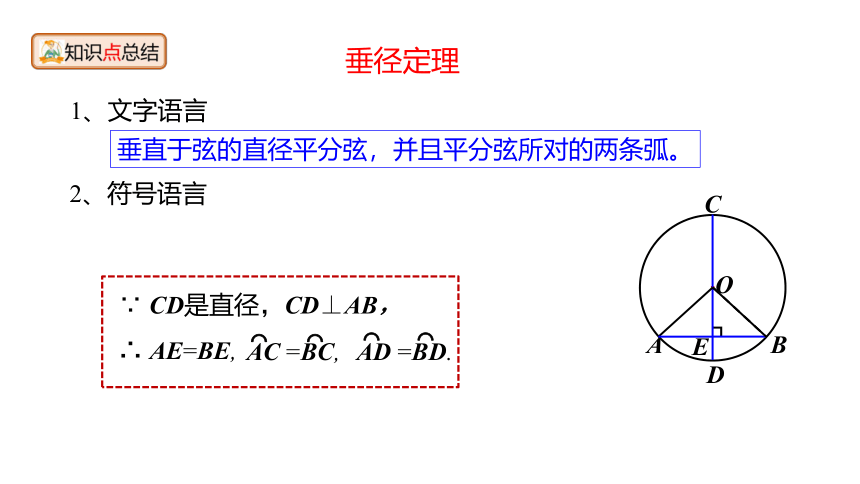
垂径定理
1、文字语言
2、符号语言
垂直于弦的直径平分弦,并且平分弦所对的两条弧。
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
·
O
A
B
C
D
E
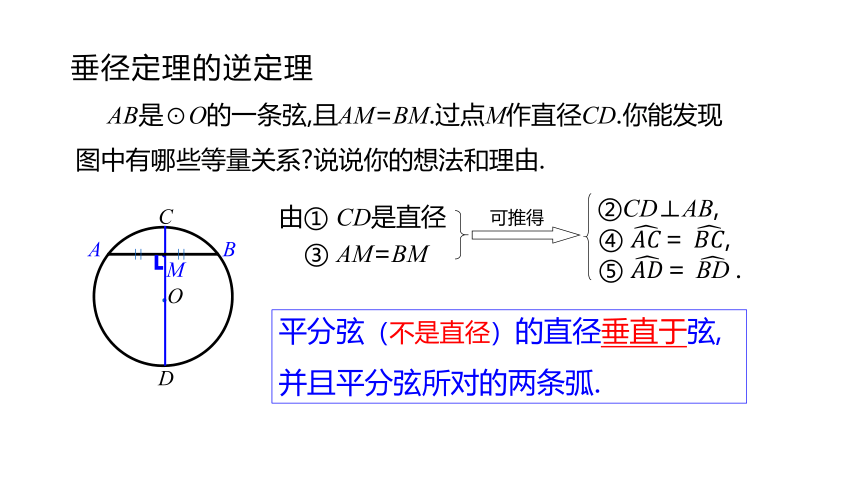
垂径定理的逆定理
AB是⊙O的一条弦,且AM=BM.过点M作直径CD.你能发现图中有哪些等量关系 说说你的想法和理由.
②CD⊥AB,
由① CD是直径
③ AM=BM
可推得
④ = ,
⑤ = .
●O
C
D
●
M
A
B
┗
平分弦(不是直径)的直径垂直于弦,
并且平分弦所对的两条弧.
垂径定理的本质是:
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
知二推三
判断下列图是否是表示垂径定理的图形。
是
不是
是
练一练
例1 如图,已知在⊙O中,弦AB的长为8cm,CD是⊙O的直径,CD⊥AB,垂足为E,DE=2cm,求⊙O的直径CD的长。
.
A
E
B
O
C
┐
例题讲解
D
解:连接OA,∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
∴ CD=2r=10cm
例2 证明:圆的两条平行弦所夹弧相等.
·
A
B
C
D
O
E
F
证明:
作直径EF 垂直于弦AB,
由于AB∥CD,因此 EF⊥CD.
从而
即
因此
由于 EF⊥CD
由于EF⊥AB,因此,
已知:如图,圆O 中,弦AB与弦CD 平行.
求证:=
例3 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以AC=BD.
E
.
A
C
D
B
O
证明:过O作OE⊥AB,垂足为E,
┐
1、如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是 ( )
A.∠COE=∠DOE
B.CE=DE
C.OE=AE
D.BD=BC
⌒
⌒
·
O
A
B
E
C
D
C
随堂演练
2、如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= cm。
·
O
A
B
E
解:连接OA,∵ OE⊥AB
∴
∴ AB=2AE=16cm
16
3.如图,在半径为5 cm的⊙O中,弦AB=6 cm,OC⊥AB于点C,则OC的长为( )
A.3 cm B.4 cm C.5 cm D.6 cm
B
4.一条排水管的截面如图所示,已知排水管的半径OA=1 m,水面宽AB=1.2 m,某天下雨后,水管内水面上升了0.2 m,则此时排水管的水面宽CD=____m.
1.6
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
两条辅助线:连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
课后小结
第2章 圆
2.3 垂径定理
问题:左图中AB为圆O的直径,CD为圆O的弦,与直径AB相交于点E,当弦CD在圆上运动的过程中有没有特殊情况?
直径AB和弦CD互相垂直
情景引入
E
A
O
D
B
C
在⊙O中,AB为弦,CD为直径,AB⊥CD
提问:你在圆中还能找到那些相等的量?并证明你猜得的结论。
线段:AE=BE
弧: = , =
获取新知
E
D
C
O
A
B
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE,= , = 。
证明:连结OA、OB,则OA=OB.
∴△OAB是等腰三角形.
∵OE⊥AB,
∴AE=BE,∠AOE=∠BOE ,
∴∠AOC=∠BOC ,
∴ = , = .
C
.
O
A
E
B
D
┗
垂径定理
1、文字语言
2、符号语言
垂直于弦的直径平分弦,并且平分弦所对的两条弧。
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
·
O
A
B
C
D
E
垂径定理的逆定理
AB是⊙O的一条弦,且AM=BM.过点M作直径CD.你能发现图中有哪些等量关系 说说你的想法和理由.
②CD⊥AB,
由① CD是直径
③ AM=BM
可推得
④ = ,
⑤ = .
●O
C
D
●
M
A
B
┗
平分弦(不是直径)的直径垂直于弦,
并且平分弦所对的两条弧.
垂径定理的本质是:
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦
(4)这条直线平分弦所对的优弧
(5)这条直线平分弦所对的劣弧
知二推三
判断下列图是否是表示垂径定理的图形。
是
不是
是
练一练
例1 如图,已知在⊙O中,弦AB的长为8cm,CD是⊙O的直径,CD⊥AB,垂足为E,DE=2cm,求⊙O的直径CD的长。
.
A
E
B
O
C
┐
例题讲解
D
解:连接OA,∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
∴ CD=2r=10cm
例2 证明:圆的两条平行弦所夹弧相等.
·
A
B
C
D
O
E
F
证明:
作直径EF 垂直于弦AB,
由于AB∥CD,因此 EF⊥CD.
从而
即
因此
由于 EF⊥CD
由于EF⊥AB,因此,
已知:如图,圆O 中,弦AB与弦CD 平行.
求证:=
例3 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以AC=BD.
E
.
A
C
D
B
O
证明:过O作OE⊥AB,垂足为E,
┐
1、如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是 ( )
A.∠COE=∠DOE
B.CE=DE
C.OE=AE
D.BD=BC
⌒
⌒
·
O
A
B
E
C
D
C
随堂演练
2、如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= cm。
·
O
A
B
E
解:连接OA,∵ OE⊥AB
∴
∴ AB=2AE=16cm
16
3.如图,在半径为5 cm的⊙O中,弦AB=6 cm,OC⊥AB于点C,则OC的长为( )
A.3 cm B.4 cm C.5 cm D.6 cm
B
4.一条排水管的截面如图所示,已知排水管的半径OA=1 m,水面宽AB=1.2 m,某天下雨后,水管内水面上升了0.2 m,则此时排水管的水面宽CD=____m.
1.6
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
两条辅助线:连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
课后小结
