湘教版数学九年级下册2.5.2 第2课时 切线的性质 同步课件(共14张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.5.2 第2课时 切线的性质 同步课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:22:38 | ||
图片预览


文档简介
(共14张PPT)
第2章 圆
2.5.2 第2课时 切线的性质
知识回顾
思考:
1.什么是圆的切线 判断一条直线是圆的切线有哪些方法
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.
即经过半径的外端并且垂直这条半径的直线是圆的切线
2.前面我们已学过的切线的性质有哪些?
答:
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
3.切线还有什么性质?
获取新知
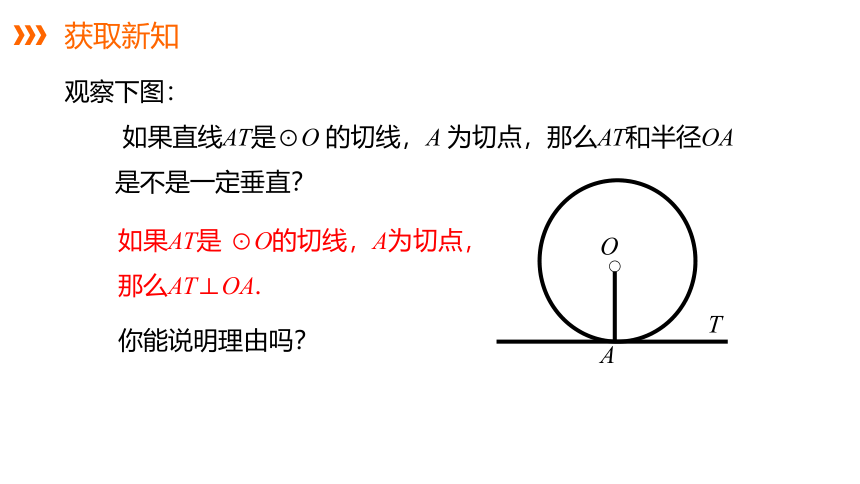
观察下图:
如果直线AT是⊙O 的切线,A 为切点,那么AT和半径OA是不是一定垂直?
A
T
O
如果AT是 ⊙O的切线,A为切点,那么AT⊥OA.
你能说明理由吗?
A
T
M
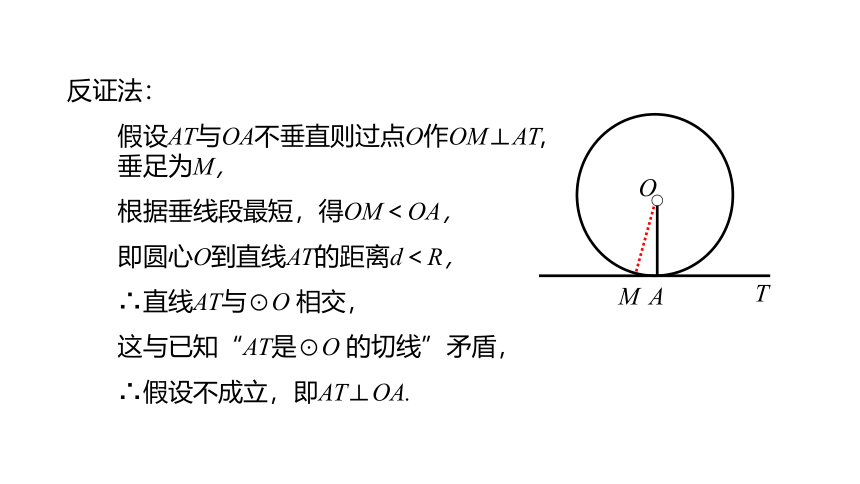
反证法:
假设AT与OA不垂直则过点O作OM⊥AT,垂足为M,
根据垂线段最短,得OM<OA,
即圆心O到直线AT的距离d<R,
∴直线AT与⊙O 相交,
这与已知“AT是⊙O 的切线”矛盾,
∴假设不成立,即AT⊥OA.
O
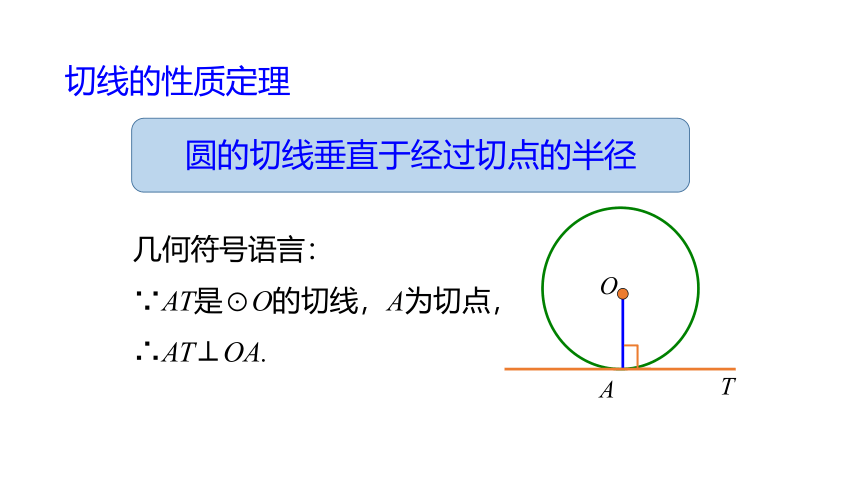
几何符号语言:
∵AT是⊙O的切线,A为切点,
∴AT⊥OA.
O
A
T
切线的性质定理
圆的切线垂直于经过切点的半径
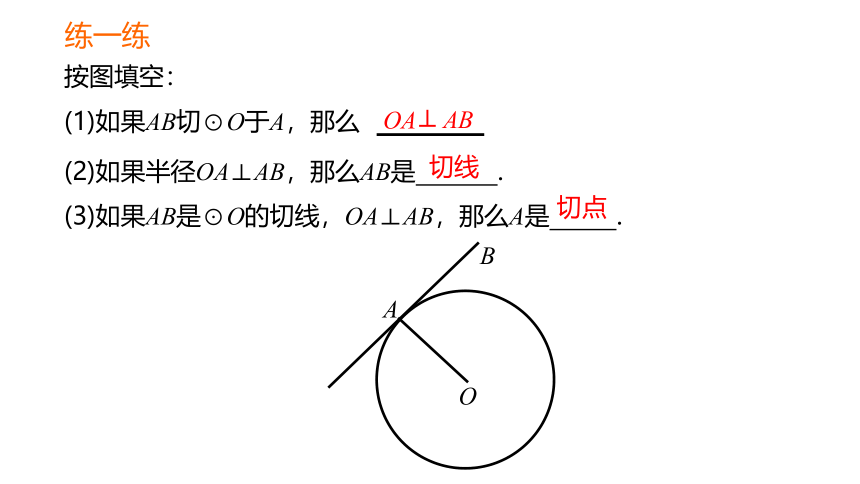
练一练
按图填空:
(1)如果AB切⊙O于A,那么
A
O
B
(2)如果半径OA⊥AB,那么AB是 .
切点
(3)如果AB是⊙O的切线,OA⊥AB,那么A是 .
切线
⊥
OA
AB.
例题讲解
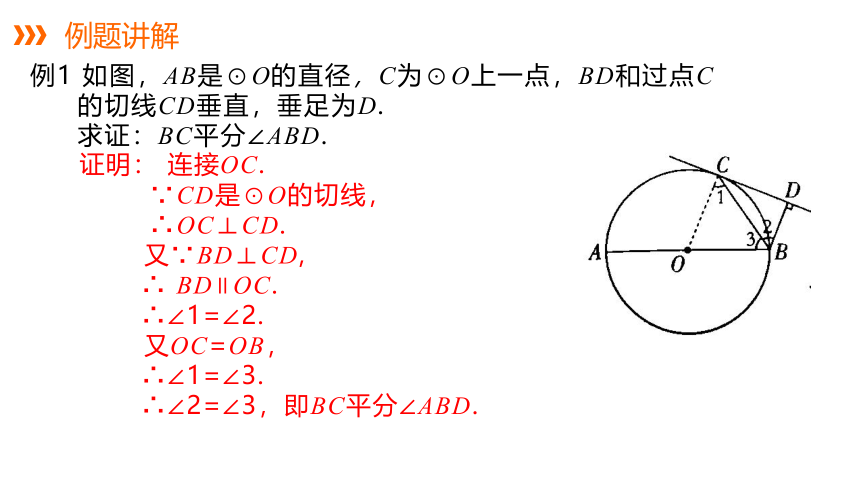
例1 如图,AB是⊙O的直径,C为⊙O上一点,BD和过点C的切线CD垂直,垂足为D.
求证:BC平分∠ABD.
证明: 连接OC.
∵CD是⊙O的切线,
∴OC⊥CD.
又∵BD⊥CD,
∴ BD∥OC.
∴∠1=∠2.
又OC=OB,
∴∠1=∠3.
∴∠2=∠3,即BC平分∠ABD.
l1
O
B
A
l2
例2 证明:经过直径两端点的切线互相平行.
已知:如图,AB是圆O的直径,l1,l2分别是经过点A,B的切线.
求证:l1//l2.
证明:∵AB是圆O的直径,l1是过点A的切线,
∴ l1⊥OA.
同理 l2⊥OB.
∴ l1⊥AB,且l2⊥AB.
∴ l1//l2.
例3 如图,AB是⊙O的直径,DC切⊙O于点C,连接CA,CB,AB=12 cm,∠ACD=30°,求AC的长.
解:连接OC.因为DC是⊙O的切线,
所以OC⊥DC,而∠ACD=30°.
所以∠ACO=60°.
又因为OA=OC,
所以△AOC是等边三角形,
所以AC=OA=AB= ×12=6(cm).
切线性质的应用及辅助线的作法:
(1)如果一条直线符合下列三个条件中的任意两个,那么它一定满足第三个条件,这三个条件是:①直线过圆心;
②直线过切点;③直线与圆的切线垂直.
(2)辅助线的作法:连切点、圆心,得垂直关系.
随堂演练
1.如图1,P是⊙O的直径AB延长线上的一点,PC与⊙O相切于点C.若∠P=20°,则∠A=____°.
2.如图2,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为______(结果保留π).
35
图1
6π
图2
3.如图,AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于点C,AB=6 cm,PB=8 cm,则BC=____cm.
4.8
4.已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求OB的长.
解:因为AB与⊙O相切于点C,
所以OC⊥AB.
因为OA=OB,
所以C是AB的中点.
由已知,得OC=2,BC=4.
在Rt△OBC中,由勾股定理,
得OB==2 .
课堂小结
①切线和圆有且只有一个公共点
③圆的切线垂直于经过切点的半径
②切线和圆心的距离等于半径
1.切线性质:
2.能运用切线性质定理进行计算与证明
3.掌握常见的关于切线辅助线作法
第2章 圆
2.5.2 第2课时 切线的性质
知识回顾
思考:
1.什么是圆的切线 判断一条直线是圆的切线有哪些方法
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.
即经过半径的外端并且垂直这条半径的直线是圆的切线
2.前面我们已学过的切线的性质有哪些?
答:
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
3.切线还有什么性质?
获取新知
观察下图:
如果直线AT是⊙O 的切线,A 为切点,那么AT和半径OA是不是一定垂直?
A
T
O
如果AT是 ⊙O的切线,A为切点,那么AT⊥OA.
你能说明理由吗?
A
T
M
反证法:
假设AT与OA不垂直则过点O作OM⊥AT,垂足为M,
根据垂线段最短,得OM<OA,
即圆心O到直线AT的距离d<R,
∴直线AT与⊙O 相交,
这与已知“AT是⊙O 的切线”矛盾,
∴假设不成立,即AT⊥OA.
O
几何符号语言:
∵AT是⊙O的切线,A为切点,
∴AT⊥OA.
O
A
T
切线的性质定理
圆的切线垂直于经过切点的半径
练一练
按图填空:
(1)如果AB切⊙O于A,那么
A
O
B
(2)如果半径OA⊥AB,那么AB是 .
切点
(3)如果AB是⊙O的切线,OA⊥AB,那么A是 .
切线
⊥
OA
AB.
例题讲解
例1 如图,AB是⊙O的直径,C为⊙O上一点,BD和过点C的切线CD垂直,垂足为D.
求证:BC平分∠ABD.
证明: 连接OC.
∵CD是⊙O的切线,
∴OC⊥CD.
又∵BD⊥CD,
∴ BD∥OC.
∴∠1=∠2.
又OC=OB,
∴∠1=∠3.
∴∠2=∠3,即BC平分∠ABD.
l1
O
B
A
l2
例2 证明:经过直径两端点的切线互相平行.
已知:如图,AB是圆O的直径,l1,l2分别是经过点A,B的切线.
求证:l1//l2.
证明:∵AB是圆O的直径,l1是过点A的切线,
∴ l1⊥OA.
同理 l2⊥OB.
∴ l1⊥AB,且l2⊥AB.
∴ l1//l2.
例3 如图,AB是⊙O的直径,DC切⊙O于点C,连接CA,CB,AB=12 cm,∠ACD=30°,求AC的长.
解:连接OC.因为DC是⊙O的切线,
所以OC⊥DC,而∠ACD=30°.
所以∠ACO=60°.
又因为OA=OC,
所以△AOC是等边三角形,
所以AC=OA=AB= ×12=6(cm).
切线性质的应用及辅助线的作法:
(1)如果一条直线符合下列三个条件中的任意两个,那么它一定满足第三个条件,这三个条件是:①直线过圆心;
②直线过切点;③直线与圆的切线垂直.
(2)辅助线的作法:连切点、圆心,得垂直关系.
随堂演练
1.如图1,P是⊙O的直径AB延长线上的一点,PC与⊙O相切于点C.若∠P=20°,则∠A=____°.
2.如图2,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为______(结果保留π).
35
图1
6π
图2
3.如图,AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于点C,AB=6 cm,PB=8 cm,则BC=____cm.
4.8
4.已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求OB的长.
解:因为AB与⊙O相切于点C,
所以OC⊥AB.
因为OA=OB,
所以C是AB的中点.
由已知,得OC=2,BC=4.
在Rt△OBC中,由勾股定理,
得OB==2 .
课堂小结
①切线和圆有且只有一个公共点
③圆的切线垂直于经过切点的半径
②切线和圆心的距离等于半径
1.切线性质:
2.能运用切线性质定理进行计算与证明
3.掌握常见的关于切线辅助线作法
