湘教版数学九年级下册2.5.2 第1课时 切线的判定 同步课件(共16张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.5.2 第1课时 切线的判定 同步课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 402.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:25:38 | ||
图片预览



文档简介
(共16张PPT)
第2章 圆
2.5.2 第1课时 切线的判定
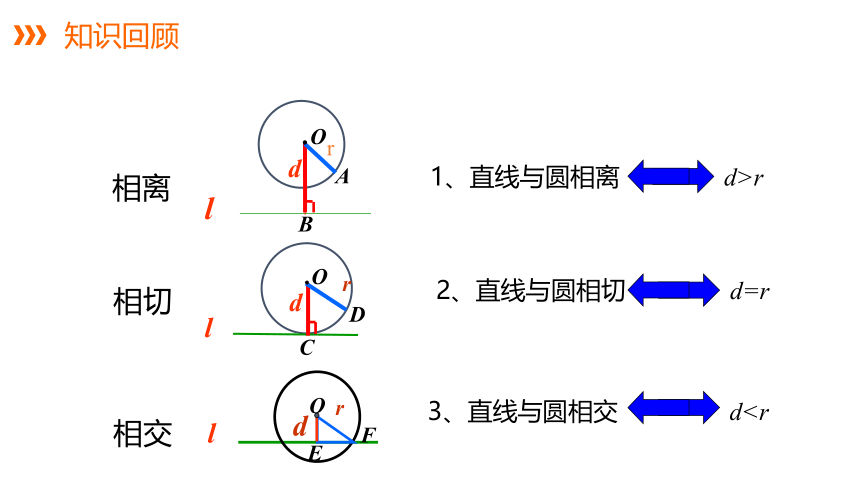
知识回顾
d
r
相离
A
d
r
相切
l
l
D
.O
r
d
相交
C
.O
B
E
F
O
1、直线与圆相离 d>r
3、直线与圆相交 dl
2、直线与圆相切 d=r
情景引入
只要你认真听完今天的课你就会明白!
问题:
1.当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2.砂轮打磨工件飞出火星的方向是什么方向?
新知探究
O
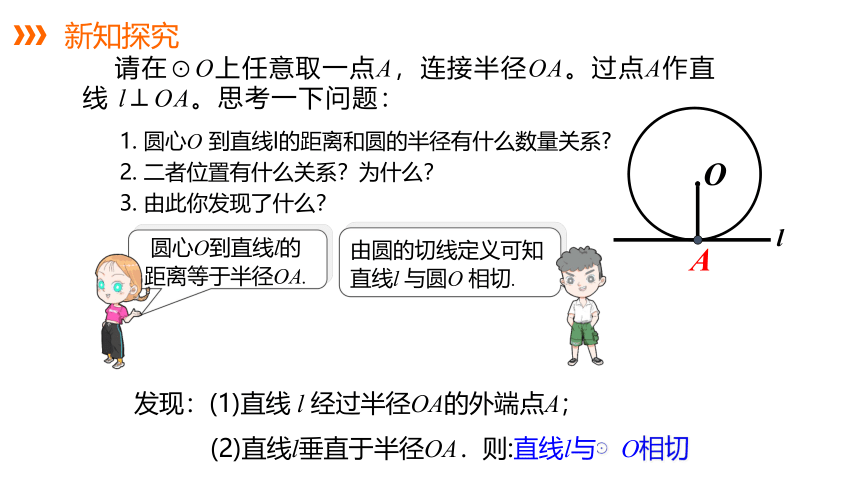
请在⊙O上任意取一点A,连接半径OA。过点A作直线 l⊥OA。思考一下问题:
1. 圆心O 到直线l的距离和圆的半径有什么数量关系
2. 二者位置有什么关系?为什么?
3. 由此你发现了什么?
l
A
圆心O到直线l的
距离等于半径OA.
由圆的切线定义可知直线l 与圆O 相切.
发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径OA.则:直线l与⊙O相切
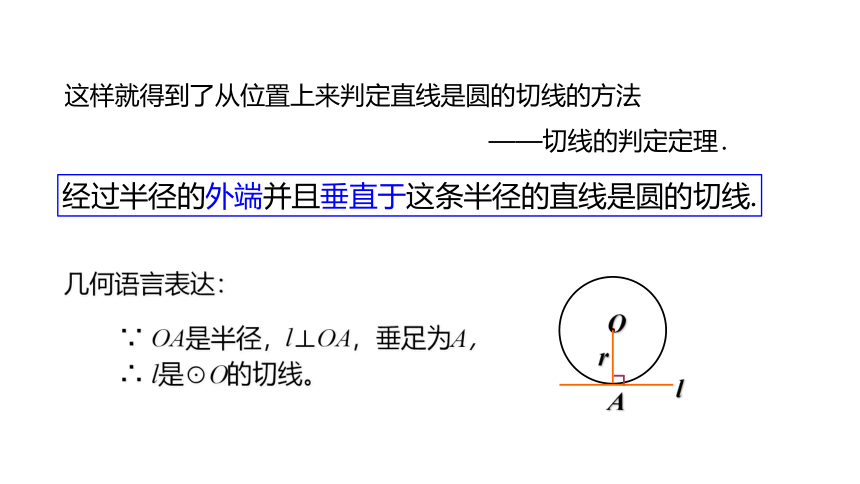
这样就得到了从位置上来判定直线是圆的切线的方法
——切线的判定定理.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
r
l
O
A
∵ OA是半径,l⊥OA,垂足为A,
∴ l是⊙O的切线。
几何语言表达:
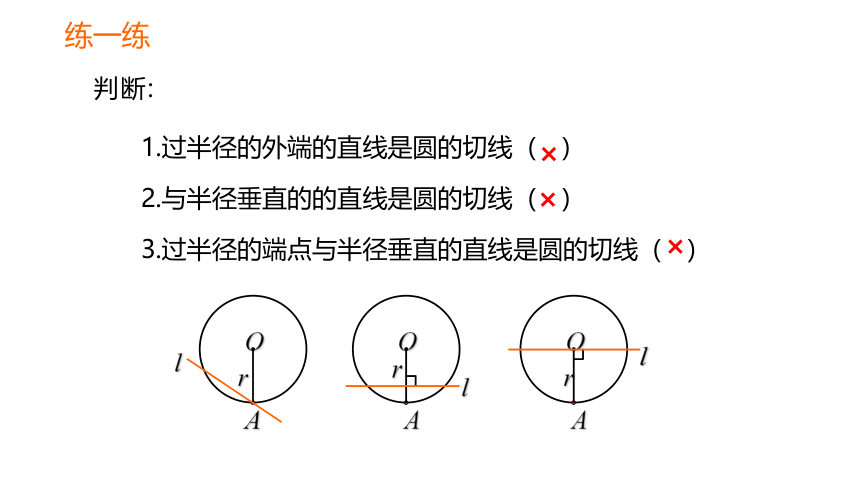
练一练
判断:
1.过半径的外端的直线是圆的切线( )
2.与半径垂直的的直线是圆的切线( )
3.过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直.
判断一条直线是圆的切线,你现在有几种方法
有三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线;
2.利用d与r的关系作判断:当d=r时直线是圆的切线;
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
直线l就是所求作的切线,如图
·
O
·
A
l
过圆O上一点A 画圆O 的切线.
画法:
⑴连结OA;
⑵过点A作直线l与OA垂直.
例题讲解
∴直线BC 是圆O 的切线.
例1 已知:如图,AD 是圆O 的直径,直线BC 经过点D,且AB=AC,∠BAD=∠CAD.
求证: 直线BC是圆O的切线.
证明:∵ AB=AC, ∠BAD=∠CAD,
∴AD⊥BC.
于是OD⊥BC.
又∵OD 是圆O的半径,且BC经过点D,
·
1
2
A
B
D
C
例2 已知:如图所示,在△ABC中,AB=AC,O是BC的中点,OD⊥AB,垂足为D,以点O为圆心,OD为半径作⊙O.
求证:AC与⊙O相切.
证明:如图,连接OA,过点O
作OE⊥AC,垂足为E.
∵AB=AC,O是BC的中点,
∴∠BAO=∠CAO.
又∵ OD⊥AB,OE⊥AC,垂足分别为D,E,
∴ OE=OD,∴ AC与⊙O相切.
判定圆的切线的常用辅助线的选择:
(1)如果已知直线过圆上一点,那么连接这点和圆心,得到半径,证明这条半径垂直于已知直线即可
可记为:有交点,作半径,证垂直;
(2)如果已知直线与圆没有明确是否有公共点,那么过圆心作已知直线的垂线段,证明垂线段的长等于半径即可
可记为:无交点,作垂线,证半径.
1.下列说法中,不正确的是( )
A.与圆只有一个交点的直线是圆的切线
B. 经过半径的外端,且垂直于这条半径的直线是圆的切线
C. 圆心到一条直线的距离等于这个圆的半径,则这条直线是圆的切线
D. 垂直于半径的直线是圆的切线
随堂演练
D
2.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为______.
相切
3.如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.
求证:AD是半圆O的切线.
证明:∵AB为半圆O的直径,
∴∠BCA=90°.
又∵BC∥OD,
∴∠OEA=∠BCA=90°,
∴∠D+∠DAE=90°,即AB⊥AD.
∵∠D=∠BAC,
∴∠BAC+∠DAE=90°.
∵AB为半圆O的直径,∴AD是半圆O的切线.
课后小结
1.判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是切线
2.常用的添辅助线方法?
⑴直线与圆的公共点已知时,则连半径,证垂直.
⑵直线与圆的公共点不确定时,则作垂直,证半径.
l是切线
l是切线
第2章 圆
2.5.2 第1课时 切线的判定
知识回顾
d
r
相离
A
d
r
相切
l
l
D
.O
r
d
相交
C
.O
B
E
F
O
1、直线与圆相离 d>r
3、直线与圆相交 d
2、直线与圆相切 d=r
情景引入
只要你认真听完今天的课你就会明白!
问题:
1.当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2.砂轮打磨工件飞出火星的方向是什么方向?
新知探究
O
请在⊙O上任意取一点A,连接半径OA。过点A作直线 l⊥OA。思考一下问题:
1. 圆心O 到直线l的距离和圆的半径有什么数量关系
2. 二者位置有什么关系?为什么?
3. 由此你发现了什么?
l
A
圆心O到直线l的
距离等于半径OA.
由圆的切线定义可知直线l 与圆O 相切.
发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径OA.则:直线l与⊙O相切
这样就得到了从位置上来判定直线是圆的切线的方法
——切线的判定定理.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
r
l
O
A
∵ OA是半径,l⊥OA,垂足为A,
∴ l是⊙O的切线。
几何语言表达:
练一练
判断:
1.过半径的外端的直线是圆的切线( )
2.与半径垂直的的直线是圆的切线( )
3.过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直.
判断一条直线是圆的切线,你现在有几种方法
有三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线;
2.利用d与r的关系作判断:当d=r时直线是圆的切线;
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
直线l就是所求作的切线,如图
·
O
·
A
l
过圆O上一点A 画圆O 的切线.
画法:
⑴连结OA;
⑵过点A作直线l与OA垂直.
例题讲解
∴直线BC 是圆O 的切线.
例1 已知:如图,AD 是圆O 的直径,直线BC 经过点D,且AB=AC,∠BAD=∠CAD.
求证: 直线BC是圆O的切线.
证明:∵ AB=AC, ∠BAD=∠CAD,
∴AD⊥BC.
于是OD⊥BC.
又∵OD 是圆O的半径,且BC经过点D,
·
1
2
A
B
D
C
例2 已知:如图所示,在△ABC中,AB=AC,O是BC的中点,OD⊥AB,垂足为D,以点O为圆心,OD为半径作⊙O.
求证:AC与⊙O相切.
证明:如图,连接OA,过点O
作OE⊥AC,垂足为E.
∵AB=AC,O是BC的中点,
∴∠BAO=∠CAO.
又∵ OD⊥AB,OE⊥AC,垂足分别为D,E,
∴ OE=OD,∴ AC与⊙O相切.
判定圆的切线的常用辅助线的选择:
(1)如果已知直线过圆上一点,那么连接这点和圆心,得到半径,证明这条半径垂直于已知直线即可
可记为:有交点,作半径,证垂直;
(2)如果已知直线与圆没有明确是否有公共点,那么过圆心作已知直线的垂线段,证明垂线段的长等于半径即可
可记为:无交点,作垂线,证半径.
1.下列说法中,不正确的是( )
A.与圆只有一个交点的直线是圆的切线
B. 经过半径的外端,且垂直于这条半径的直线是圆的切线
C. 圆心到一条直线的距离等于这个圆的半径,则这条直线是圆的切线
D. 垂直于半径的直线是圆的切线
随堂演练
D
2.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为______.
相切
3.如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.
求证:AD是半圆O的切线.
证明:∵AB为半圆O的直径,
∴∠BCA=90°.
又∵BC∥OD,
∴∠OEA=∠BCA=90°,
∴∠D+∠DAE=90°,即AB⊥AD.
∵∠D=∠BAC,
∴∠BAC+∠DAE=90°.
∵AB为半圆O的直径,∴AD是半圆O的切线.
课后小结
1.判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是切线
2.常用的添辅助线方法?
⑴直线与圆的公共点已知时,则连半径,证垂直.
⑵直线与圆的公共点不确定时,则作垂直,证半径.
l是切线
l是切线
