湘教版数学九年级下册2.5.1 直线与圆的位置关系 同步课件(共14张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.5.1 直线与圆的位置关系 同步课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 301.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第2章 圆
2.5.1 直线与圆的位置关系
知识回顾
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r
点在圆上 d=r
点在圆内 dA
B
C
位置关系
数形结合:
数量关系
情景引入
请同学们利用手中的工具再现海上日出的整个情景。
在再现过程中,你认为直线与圆的位置关系可以分为哪几类?你分类的依据是什么?
(地平线)
a(地平线)
●O
●O
●O
获取新知
(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(1)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点.
(3)直线和圆没有公共点时,叫做直线和圆相离.
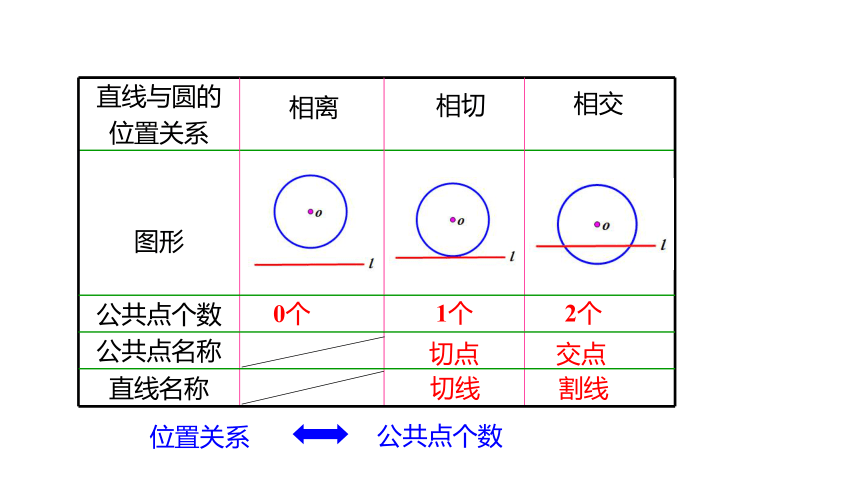
一、直线与圆的位置关系(用公共点的个数来区分)
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
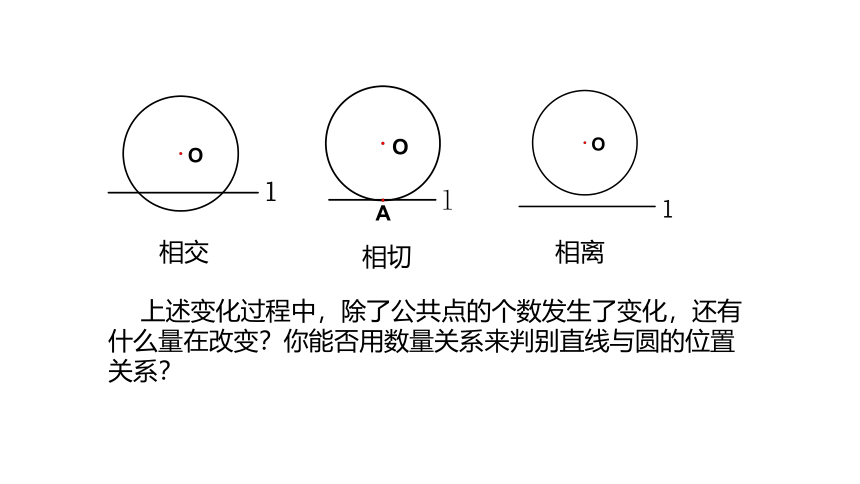
相交
相切
相离
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
新知探究
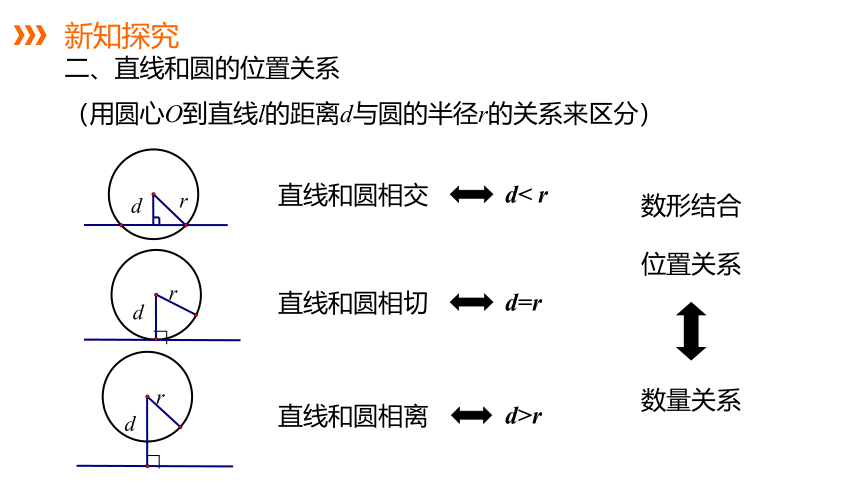
直线和圆相交
d< r
直线和圆相切
d=r
直线和圆相离
d>r
r
d
∟
r
d
∟
r
d
数形结合
位置关系
数量关系
二、直线和圆的位置关系
(用圆心O到直线l的距离d与圆的半径r的关系来区分)
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由___________________的个数来判断;
(2)根据性质,由____________________________ 的关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
例题讲解
例1 如图,∠C=30°,O为BC上一点,且CO=6cm,以O为圆心,r为半径的圆与直线CA有怎样的位置关系?为什么?
(1)r=2.5cm;(2)r=3cm;(3)r=5cm.
解:过O点作OD⊥CA交CA于D.
A
B
C
D
O
在Rt△CDO中, ∠C=30°,
即圆心O到直线CA的距离d=3cm.
(1)r=2.5cm时,有d>r,因此⊙O与直线CA相离;
(2)r=3cm时,有d=r,因此⊙O与直线CA相切;
(3)r=5cm时,有d<r,因此⊙O与直线CA相交.
∴
例2 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.若以点C为圆心,r为半径作圆,则
(1)当直线AB与⊙C相切时,求r的值;
(2)当直线AB与⊙C相离时,求r的取值范围.
解:(1)过点C作CD⊥AB于点D.
∵在Rt△ABC中,AC=3,AB=5,
∴BC==4.
∵AC·BC= AB·CD,∴CD=d=2.4.
∵当直线AB与⊙C相切时,d=r,∴r=2.4.
(2)由(1)知,圆心C到直线AB的距离d=2.4.
∵当直线AB与⊙C相离时,d>r,∴0随堂演练
1.已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8cm,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm,则直线与圆 , 直线与圆有 个公共点.
3)若AB和⊙O相交,则 .
2.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d,根据条件
填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
0cm≤
2
1
0
3.如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,以C为圆心的圆与AB相切,则这个圆的半径是 cm.
4.直线l 和⊙O有公共点,则直线l 与⊙O( )
A.相离 B.相切 C.相交 D.相切或相交
2.4
D
5.在同一平面内,已知点O到直线l的距离为6,以点O为圆心,r为半径画圆.
(1)当r=___时,⊙O上有且只有1个点到直线l的距离等于2;
(2)若⊙O上有且只有2个点到直线l的距离为2,则r的取值范围是________.
4
4<r<8
课堂小结
直线与圆的位置关系
类型
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:在图中没有d要先做出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
d
第2章 圆
2.5.1 直线与圆的位置关系
知识回顾
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r
点在圆上 d=r
点在圆内 d
B
C
位置关系
数形结合:
数量关系
情景引入
请同学们利用手中的工具再现海上日出的整个情景。
在再现过程中,你认为直线与圆的位置关系可以分为哪几类?你分类的依据是什么?
(地平线)
a(地平线)
●O
●O
●O
获取新知
(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(1)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点.
(3)直线和圆没有公共点时,叫做直线和圆相离.
一、直线与圆的位置关系(用公共点的个数来区分)
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
相交
相切
相离
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
新知探究
直线和圆相交
d< r
直线和圆相切
d=r
直线和圆相离
d>r
r
d
∟
r
d
∟
r
d
数形结合
位置关系
数量关系
二、直线和圆的位置关系
(用圆心O到直线l的距离d与圆的半径r的关系来区分)
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由___________________的个数来判断;
(2)根据性质,由____________________________ 的关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
例题讲解
例1 如图,∠C=30°,O为BC上一点,且CO=6cm,以O为圆心,r为半径的圆与直线CA有怎样的位置关系?为什么?
(1)r=2.5cm;(2)r=3cm;(3)r=5cm.
解:过O点作OD⊥CA交CA于D.
A
B
C
D
O
在Rt△CDO中, ∠C=30°,
即圆心O到直线CA的距离d=3cm.
(1)r=2.5cm时,有d>r,因此⊙O与直线CA相离;
(2)r=3cm时,有d=r,因此⊙O与直线CA相切;
(3)r=5cm时,有d<r,因此⊙O与直线CA相交.
∴
例2 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.若以点C为圆心,r为半径作圆,则
(1)当直线AB与⊙C相切时,求r的值;
(2)当直线AB与⊙C相离时,求r的取值范围.
解:(1)过点C作CD⊥AB于点D.
∵在Rt△ABC中,AC=3,AB=5,
∴BC==4.
∵AC·BC= AB·CD,∴CD=d=2.4.
∵当直线AB与⊙C相切时,d=r,∴r=2.4.
(2)由(1)知,圆心C到直线AB的距离d=2.4.
∵当直线AB与⊙C相离时,d>r,∴0
1.已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8cm,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm,则直线与圆 , 直线与圆有 个公共点.
3)若AB和⊙O相交,则 .
2.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d,根据条件
填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
0cm≤
2
1
0
3.如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,以C为圆心的圆与AB相切,则这个圆的半径是 cm.
4.直线l 和⊙O有公共点,则直线l 与⊙O( )
A.相离 B.相切 C.相交 D.相切或相交
2.4
D
5.在同一平面内,已知点O到直线l的距离为6,以点O为圆心,r为半径画圆.
(1)当r=___时,⊙O上有且只有1个点到直线l的距离等于2;
(2)若⊙O上有且只有2个点到直线l的距离为2,则r的取值范围是________.
4
4<r<8
课堂小结
直线与圆的位置关系
类型
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:在图中没有d要先做出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
