湘教版数学九年级下册2.5.3 切线长定理 同步课件(共16张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.5.3 切线长定理 同步课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 662.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:29:40 | ||
图片预览


文档简介
(共16张PPT)
第2章 圆
2.5.3 切线长定理
情景引入
50°
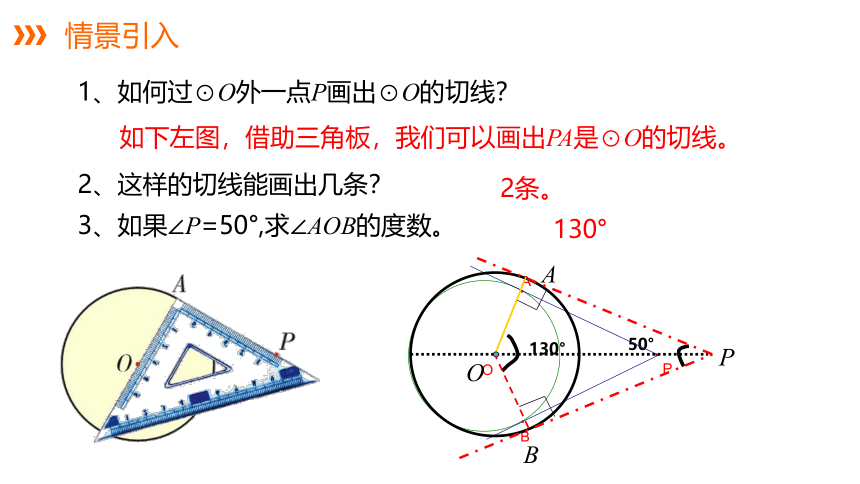
1、如何过⊙O外一点P画出⊙O的切线?
2、这样的切线能画出几条?
如下左图,借助三角板,我们可以画出PA是⊙O的切线。
3、如果∠P=50°,求∠AOB的度数。
130°
2条。
130°
O
P
A
B
获取新知
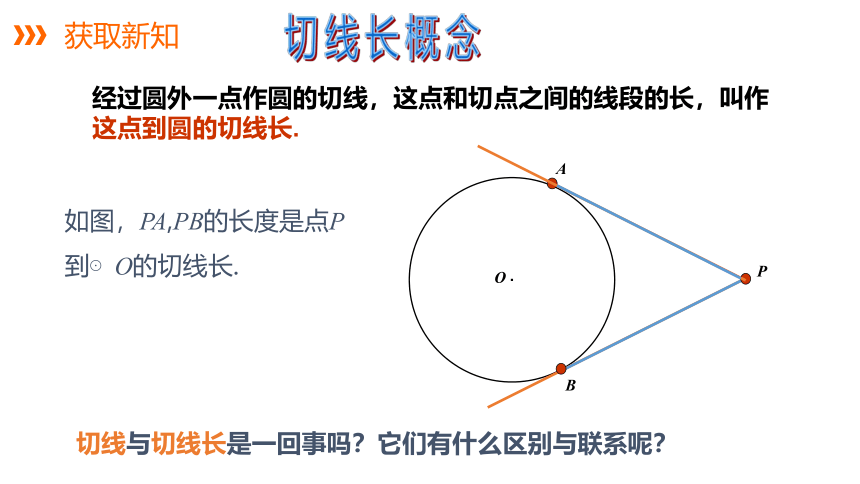
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
如图,PA,PB的长度是点P
到⊙O的切线长.
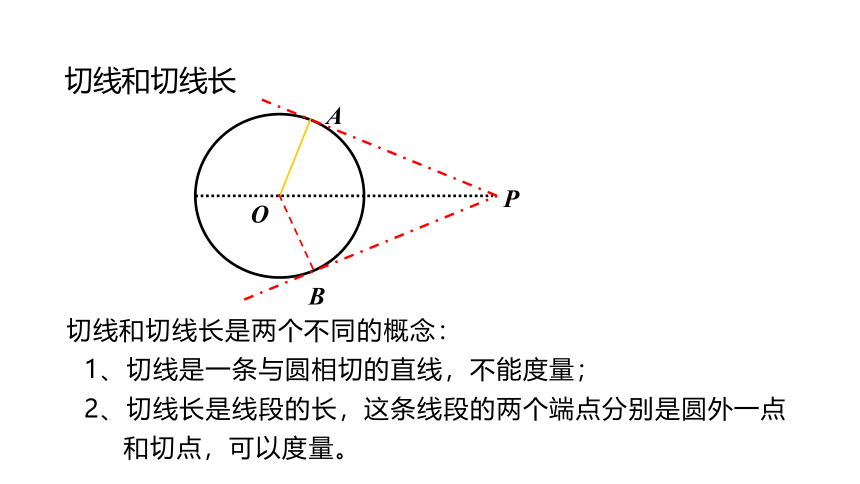
切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
O
P
A
B
切线和切线长
PA=PB,OPA=∠OPB
我们猜测过圆外一点所作的圆的两条切线长相等,这点和圆心的连线平分两条切线的夹角.接下来我们验证这个猜测.
思考:已知⊙O切线PA、PB,A、B为切点,把圆沿着直线OP对折,你能发现什么
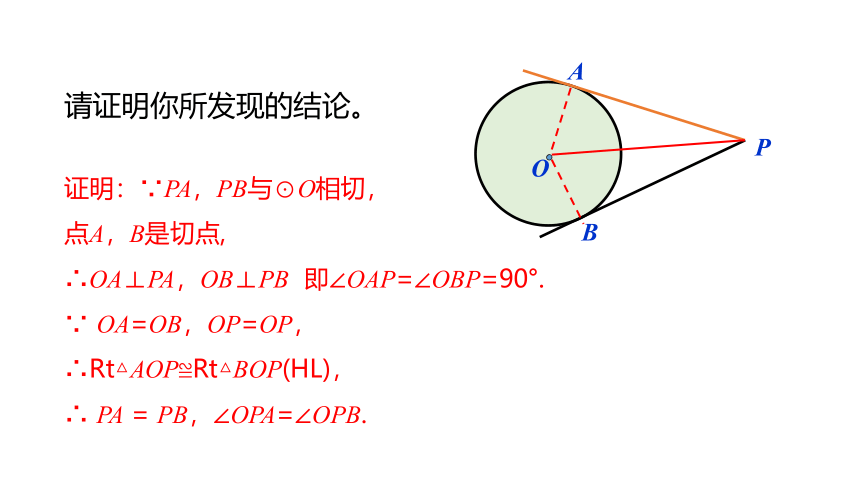
请证明你所发现的结论。
B
P
O
A
证明:∵PA,PB与⊙O相切,
点A,B是切点,
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°.
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL),
∴ PA = PB,∠OPA=∠OPB.
A
B
P
O
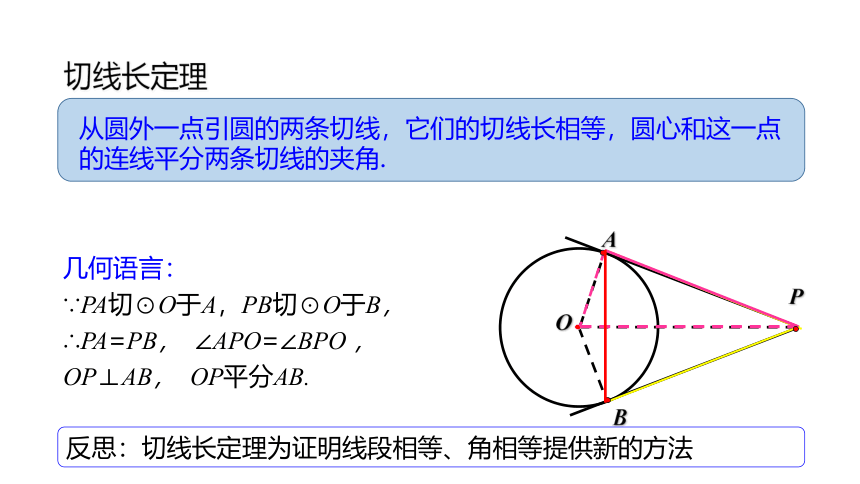
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
几何语言:
∵PA切⊙O于A,PB切⊙O于B,
∴PA=PB, ∠APO=∠BPO ,
OP⊥AB, OP平分AB.
反思:切线长定理为证明线段相等、角相等提供新的方法
切线长定理
练一练
知识点一 切线长定义
过圆外一点作圆的切线,这点和 的线段的长,叫做这点到圆的切线长.
知识点二 切线长定理
从圆外一点可以引圆的两条切线,它们的 相等;这一点和圆心的连线平分 ,垂直平分切点所成的 ,平分切点所成的两 .
切点
切线长
两条切线的夹角
弦
弧
例题讲解
例1 如图,AD是⊙O的直径,点C为⊙O外一点,CA和CB是⊙O的切线,A和B是切点,连接BD.
求证:CO∥BD.
分析:连接AB,因为AD是直径,那么∠ABD=90°,即BD⊥AB.因此要证CO∥BD,只要证CO⊥AB即可.
证明:连接AB.
∵CA和CB是⊙O的切线,点A,B为切点,
∴CA=CB,∠ACO=∠BCO.
∴CO⊥AB.
∵AD是⊙O的直径.
∴∠ABD=90°,即BD⊥AB.
∴CO∥BD.
例2 如图所示,PA,PB是⊙O的切线,切点分别是A,B,Q为上一点,过点Q作⊙O的切线,分别交PA,PB于点E,F.已知PA=12 cm,∠P=70°.求:
(1)△PEF 的周长;
(2)∠EOF 的度数.
解:(1)∵PA,PB,EF是⊙O的切线,
∴PA=PB,EA=EQ,FQ=FB,
∴△PEF的周长为PE+PF+EQ+FQ=PA+PB=24(cm).
(2)连接OA,OB,OQ.
∵PA,PB,EF是⊙O的切线,
∴PA⊥OA,PB⊥OB,EF⊥OQ,
∠AEO=∠QEO,∠QFO=∠BFO,
∴∠AOE=∠QOE,∠BOF=∠QOF.
又∵∠AOB=180°-∠P=110°,
∴∠EOF=∠AOB=55°.
解决切线长问题常见的辅助线作法:
(1)连接圆心和切点;
(2)连接两个切点;
(3)连接圆心和两切线的交点.
随堂演练
1.如图1,PA,PB切⊙O于点A,B,PA=8,CD切⊙O于点E,分别交PA,PB于点C,D,则△PCD的周长是( )
A.8 B.18 C.16 D.14
2.如图2,PA,PB分别切⊙O于点A,B,∠APB=50°,则∠AOP=____°.
C
65
图1
图2
3. 如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,F.如果AF=2cm,BD=7cm,CE=4cm,则BC=_______, AC= _____,AB=______
11cm
6cm
9cm
B
D
A
C
F
E
2
7
4
4.如图,PA,PB分别切⊙O于点A,B,连接PO与⊙O相交于点C,连接AC,BC.
求证:AC=BC.
证明:∵PA,PB分别切⊙O于点A,B,
∴PA=PB,∠APC=∠BPC.
又∵PC=PC,
∴△APC≌△BPC,
∴AC=BC.
切线长
切线长定理
作用
过圆外一点所画的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
内容
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
经过圆外一点作圆的切线,这点和切点
之间的线段的长.
课堂小结
第2章 圆
2.5.3 切线长定理
情景引入
50°
1、如何过⊙O外一点P画出⊙O的切线?
2、这样的切线能画出几条?
如下左图,借助三角板,我们可以画出PA是⊙O的切线。
3、如果∠P=50°,求∠AOB的度数。
130°
2条。
130°
O
P
A
B
获取新知
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
如图,PA,PB的长度是点P
到⊙O的切线长.
切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
O
P
A
B
切线和切线长
PA=PB,OPA=∠OPB
我们猜测过圆外一点所作的圆的两条切线长相等,这点和圆心的连线平分两条切线的夹角.接下来我们验证这个猜测.
思考:已知⊙O切线PA、PB,A、B为切点,把圆沿着直线OP对折,你能发现什么
请证明你所发现的结论。
B
P
O
A
证明:∵PA,PB与⊙O相切,
点A,B是切点,
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°.
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL),
∴ PA = PB,∠OPA=∠OPB.
A
B
P
O
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
几何语言:
∵PA切⊙O于A,PB切⊙O于B,
∴PA=PB, ∠APO=∠BPO ,
OP⊥AB, OP平分AB.
反思:切线长定理为证明线段相等、角相等提供新的方法
切线长定理
练一练
知识点一 切线长定义
过圆外一点作圆的切线,这点和 的线段的长,叫做这点到圆的切线长.
知识点二 切线长定理
从圆外一点可以引圆的两条切线,它们的 相等;这一点和圆心的连线平分 ,垂直平分切点所成的 ,平分切点所成的两 .
切点
切线长
两条切线的夹角
弦
弧
例题讲解
例1 如图,AD是⊙O的直径,点C为⊙O外一点,CA和CB是⊙O的切线,A和B是切点,连接BD.
求证:CO∥BD.
分析:连接AB,因为AD是直径,那么∠ABD=90°,即BD⊥AB.因此要证CO∥BD,只要证CO⊥AB即可.
证明:连接AB.
∵CA和CB是⊙O的切线,点A,B为切点,
∴CA=CB,∠ACO=∠BCO.
∴CO⊥AB.
∵AD是⊙O的直径.
∴∠ABD=90°,即BD⊥AB.
∴CO∥BD.
例2 如图所示,PA,PB是⊙O的切线,切点分别是A,B,Q为上一点,过点Q作⊙O的切线,分别交PA,PB于点E,F.已知PA=12 cm,∠P=70°.求:
(1)△PEF 的周长;
(2)∠EOF 的度数.
解:(1)∵PA,PB,EF是⊙O的切线,
∴PA=PB,EA=EQ,FQ=FB,
∴△PEF的周长为PE+PF+EQ+FQ=PA+PB=24(cm).
(2)连接OA,OB,OQ.
∵PA,PB,EF是⊙O的切线,
∴PA⊥OA,PB⊥OB,EF⊥OQ,
∠AEO=∠QEO,∠QFO=∠BFO,
∴∠AOE=∠QOE,∠BOF=∠QOF.
又∵∠AOB=180°-∠P=110°,
∴∠EOF=∠AOB=55°.
解决切线长问题常见的辅助线作法:
(1)连接圆心和切点;
(2)连接两个切点;
(3)连接圆心和两切线的交点.
随堂演练
1.如图1,PA,PB切⊙O于点A,B,PA=8,CD切⊙O于点E,分别交PA,PB于点C,D,则△PCD的周长是( )
A.8 B.18 C.16 D.14
2.如图2,PA,PB分别切⊙O于点A,B,∠APB=50°,则∠AOP=____°.
C
65
图1
图2
3. 如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,F.如果AF=2cm,BD=7cm,CE=4cm,则BC=_______, AC= _____,AB=______
11cm
6cm
9cm
B
D
A
C
F
E
2
7
4
4.如图,PA,PB分别切⊙O于点A,B,连接PO与⊙O相交于点C,连接AC,BC.
求证:AC=BC.
证明:∵PA,PB分别切⊙O于点A,B,
∴PA=PB,∠APC=∠BPC.
又∵PC=PC,
∴△APC≌△BPC,
∴AC=BC.
切线长
切线长定理
作用
过圆外一点所画的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
内容
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
经过圆外一点作圆的切线,这点和切点
之间的线段的长.
课堂小结
