湘教版数学九年级下册2.7正多边形与圆 同步课件(共25张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.7正多边形与圆 同步课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 887.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:31:33 | ||
图片预览






文档简介
(共25张PPT)
第2章 圆
2.7 正多边形与圆
情景引入
多姿多彩的正多边形:生活中的正多边形图案
新知探究
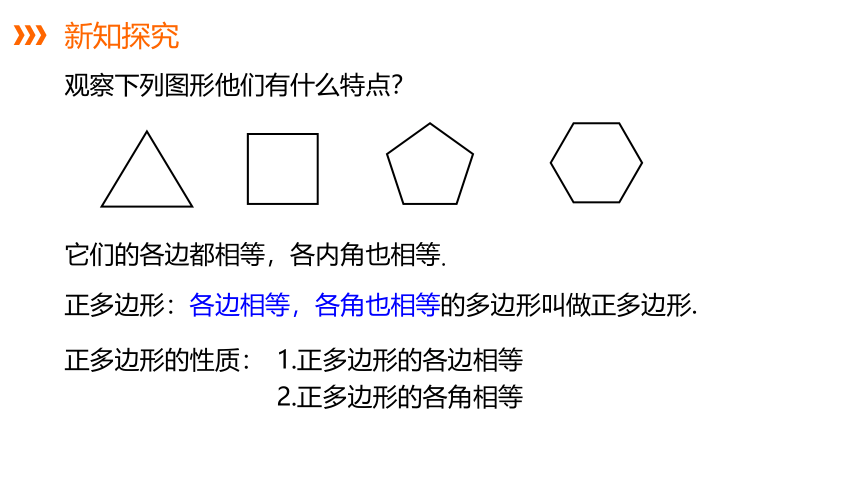
观察下列图形他们有什么特点?
它们的各边都相等,各内角也相等.
正多边形:各边相等,各角也相等的多边形叫做正多边形.
1.正多边形的各边相等
2.正多边形的各角相等
正多边形的性质:
菱形是正多边形吗?矩形呢?正方形呢 为什么?
菱形, 矩形都不是正多边形,正方形是正多边形.
×
四角不全相等
四边不全相等
四边相等,四角也相等
×
√
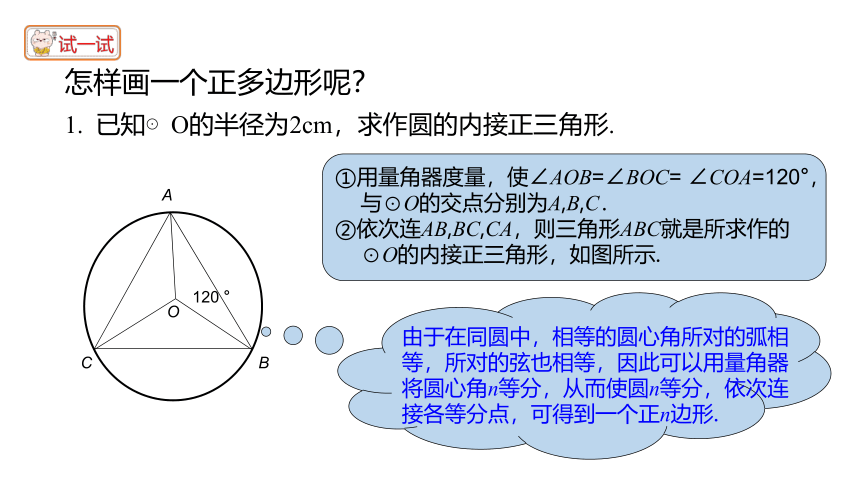
1. 已知⊙O的半径为2cm,求作圆的内接正三角形.
①用量角器度量,使∠AOB=∠BOC= ∠COA=120°,与⊙O的交点分别为A,B,C.
②依次连AB,BC,CA,则三角形ABC就是所求作的⊙O的内接正三角形,如图所示.
怎样画一个正多边形呢?
由于在同圆中,相等的圆心角所对的弧相等,所对的弦也相等,因此可以用量角器将圆心角n等分,从而使圆n等分,依次连接各等分点,可得到一个正n边形.
120 °
A
O
C
B
用量角器等分圆:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形.采用“先用量角器画一个 的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”.
这种方法简便,且可以画任意正多边形、误差小.
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
练一练
2. 已知⊙O的半径为r ,求作⊙O的内接正六边形.
分析:因为正六边形每条边所对的圆心角为 ,
所以正六边形的边长与圆的半径 .
因此,在半径为r的圆上依次截取等于 的弦,
即可将圆六等分.
60
相等
r
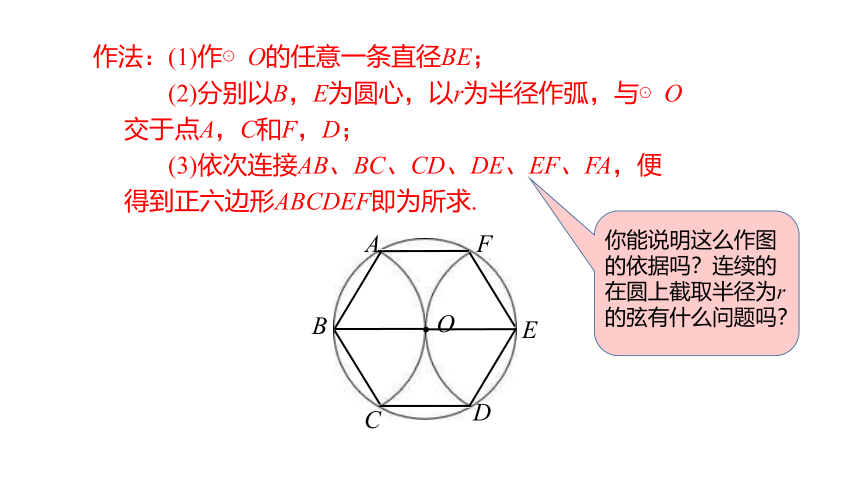
作法:(1)作⊙O的任意一条直径BE;
(2)分别以B,E为圆心,以r为半径作弧,与⊙O
交于点A,C和F,D;
(3)依次连接AB、BC、CD、DE、EF、FA,便
得到正六边形ABCDEF即为所求.
. O
B
E
C
D
F
A
你能说明这么作图的依据吗?连续的在圆上截取半径为r的弦有什么问题吗?
用尺规等分圆:
用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差.
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
将一个圆n(n≥3)等分,依次连接各等分点所得的多边形叫做这个圆的内接正多边形,这个圆叫做正多边形的外接圆。
E
F
C
D
.
O
中心角
A
B
G
边心距把△AOB分成2个全等的直角三角形
设正多边形的边长为a,半径为R,边心距为r,
R
a
面积
它的周长为L=na.
r
你能尺规作出正四边形、正八边形吗?
·
A
B
C
D
O
只要作出已知⊙O的互相垂直的直径即得圆内接正方形;
再过圆心作各边的垂线与⊙O相交(或作各中心角的角平分线与⊙O相交)即得圆内接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
练一练
轴对称图形
轴对称图形
轴对称图形;中心对称图形,对称中心为对称轴的交点
观察下列正多边形,哪些是轴对称图形,哪些是中心对称图形,并画出其对称轴或找出其对称中心.
正三角形
(奇数边)
正方形
(偶数边)
正五边形
(奇数边)
我们可以得出哪些结论?
1.正多边形都是轴对称图形。
2.当n为奇数时,正多边形仅为轴对称图形;当n为偶数时,正多边形既是轴对称图形,也是中心对称图形。
1. 正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
2. 一个正n边形绕它的中心旋转所得的图形与这个正n边形重合.
3. 边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心.此时,正n边形有条对称轴是顶点和中心的连线,有条对称轴是过中心与边垂直的直线。
4. 边数是奇数的正多边形还是中心对称图形,它的中心就是对称中心.此时,正n边形的n条对称轴是顶点与中心的连线。
正n边形(n为偶数)是中心对称图形,它的对称中心就是这个正n边形的中心.
正三角形 正方形 正五边形 正六边形
是 否 中 心 对 称 图 形
是 否 旋 转 对 称 图 形
绕 中 心 旋 转 最 少 角 度 数
×
√
×
√
√
√
√
√
120°
90°
72°
60°
归纳总结
例题讲解
例1 用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
你能简单说明下如何用尺规做出两条垂直的直径吗?
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
例2:有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
O
B
C
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
1.如图,点O是正五边形ABCDE的中心,则∠BAO的度数为_____.
54°
随堂演练
2.边长为a的正六边形的中心到边的距离是____,周长是_____,面积是________.
3.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于_____.
6a
2π
4.如图,已知圆O的半径为R,OD⊥BC于点D,
求它的内接正三角形ABC的边长.
课堂小结
圆内接正多边形
正多边形和圆的关系
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正n边形各顶点等分其外接圆.
第2章 圆
2.7 正多边形与圆
情景引入
多姿多彩的正多边形:生活中的正多边形图案
新知探究
观察下列图形他们有什么特点?
它们的各边都相等,各内角也相等.
正多边形:各边相等,各角也相等的多边形叫做正多边形.
1.正多边形的各边相等
2.正多边形的各角相等
正多边形的性质:
菱形是正多边形吗?矩形呢?正方形呢 为什么?
菱形, 矩形都不是正多边形,正方形是正多边形.
×
四角不全相等
四边不全相等
四边相等,四角也相等
×
√
1. 已知⊙O的半径为2cm,求作圆的内接正三角形.
①用量角器度量,使∠AOB=∠BOC= ∠COA=120°,与⊙O的交点分别为A,B,C.
②依次连AB,BC,CA,则三角形ABC就是所求作的⊙O的内接正三角形,如图所示.
怎样画一个正多边形呢?
由于在同圆中,相等的圆心角所对的弧相等,所对的弦也相等,因此可以用量角器将圆心角n等分,从而使圆n等分,依次连接各等分点,可得到一个正n边形.
120 °
A
O
C
B
用量角器等分圆:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形.采用“先用量角器画一个 的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”.
这种方法简便,且可以画任意正多边形、误差小.
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
练一练
2. 已知⊙O的半径为r ,求作⊙O的内接正六边形.
分析:因为正六边形每条边所对的圆心角为 ,
所以正六边形的边长与圆的半径 .
因此,在半径为r的圆上依次截取等于 的弦,
即可将圆六等分.
60
相等
r
作法:(1)作⊙O的任意一条直径BE;
(2)分别以B,E为圆心,以r为半径作弧,与⊙O
交于点A,C和F,D;
(3)依次连接AB、BC、CD、DE、EF、FA,便
得到正六边形ABCDEF即为所求.
. O
B
E
C
D
F
A
你能说明这么作图的依据吗?连续的在圆上截取半径为r的弦有什么问题吗?
用尺规等分圆:
用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差.
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
将一个圆n(n≥3)等分,依次连接各等分点所得的多边形叫做这个圆的内接正多边形,这个圆叫做正多边形的外接圆。
E
F
C
D
.
O
中心角
A
B
G
边心距把△AOB分成2个全等的直角三角形
设正多边形的边长为a,半径为R,边心距为r,
R
a
面积
它的周长为L=na.
r
你能尺规作出正四边形、正八边形吗?
·
A
B
C
D
O
只要作出已知⊙O的互相垂直的直径即得圆内接正方形;
再过圆心作各边的垂线与⊙O相交(或作各中心角的角平分线与⊙O相交)即得圆内接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
练一练
轴对称图形
轴对称图形
轴对称图形;中心对称图形,对称中心为对称轴的交点
观察下列正多边形,哪些是轴对称图形,哪些是中心对称图形,并画出其对称轴或找出其对称中心.
正三角形
(奇数边)
正方形
(偶数边)
正五边形
(奇数边)
我们可以得出哪些结论?
1.正多边形都是轴对称图形。
2.当n为奇数时,正多边形仅为轴对称图形;当n为偶数时,正多边形既是轴对称图形,也是中心对称图形。
1. 正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
2. 一个正n边形绕它的中心旋转所得的图形与这个正n边形重合.
3. 边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心.此时,正n边形有条对称轴是顶点和中心的连线,有条对称轴是过中心与边垂直的直线。
4. 边数是奇数的正多边形还是中心对称图形,它的中心就是对称中心.此时,正n边形的n条对称轴是顶点与中心的连线。
正n边形(n为偶数)是中心对称图形,它的对称中心就是这个正n边形的中心.
正三角形 正方形 正五边形 正六边形
是 否 中 心 对 称 图 形
是 否 旋 转 对 称 图 形
绕 中 心 旋 转 最 少 角 度 数
×
√
×
√
√
√
√
√
120°
90°
72°
60°
归纳总结
例题讲解
例1 用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
你能简单说明下如何用尺规做出两条垂直的直径吗?
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
例2:有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
O
B
C
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
1.如图,点O是正五边形ABCDE的中心,则∠BAO的度数为_____.
54°
随堂演练
2.边长为a的正六边形的中心到边的距离是____,周长是_____,面积是________.
3.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于_____.
6a
2π
4.如图,已知圆O的半径为R,OD⊥BC于点D,
求它的内接正三角形ABC的边长.
课堂小结
圆内接正多边形
正多边形和圆的关系
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正n边形各顶点等分其外接圆.
