湘教版数学九年级下册2.2.2圆周角定理及其推论 同步课件(共19张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.2.2圆周角定理及其推论 同步课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:33:45 | ||
图片预览




文档简介
(共19张PPT)
第2章 圆
2.2.2 圆周角定理及其推论1
复习引入
1.什么叫圆心角
.
O
A
B
顶点在圆心的角叫圆心角
2. 圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等.
.
O
A
问题:将圆心角顶点向上移,直至与⊙O相交于点C,观察得到的∠ACB有什么特征?
C
顶点在圆上
两边都与圆相交
这样的角叫圆周角.
B
探究点一 圆周角的概念
圆周角的定义:顶点在圆上,并且两边与圆相交的角叫做圆周角.
获取新知
我们把∠ACB叫作所对圆周角, 叫作圆周角∠ACB所对的弧.
探究点二 圆周角定理
圆周角在我们生活中处处可见,比如,我们从团旗上的图案抽象出如图所示图形,图形中就有很多圆周角.
E
·
A
O
D
B
C
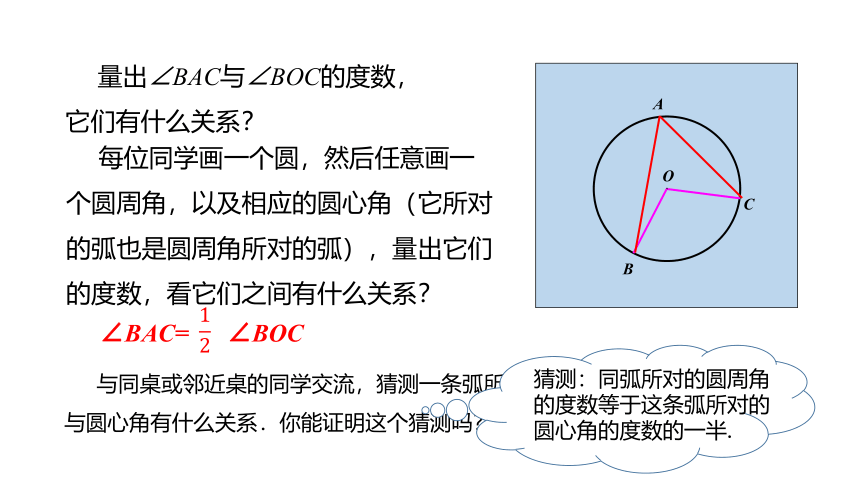
每位同学画一个圆,然后任意画一个圆周角,以及相应的圆心角(它所对的弧也是圆周角所对的弧),量出它们的度数,看它们之间有什么关系?
·
O
A
C
B
量出∠BAC与∠BOC的度数,它们有什么关系?
∠BAC= ∠BOC
与同桌或邻近桌的同学交流,猜测一条弧所对的圆周角与圆心角有什么关系.你能证明这个猜测吗?
猜测:同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半.
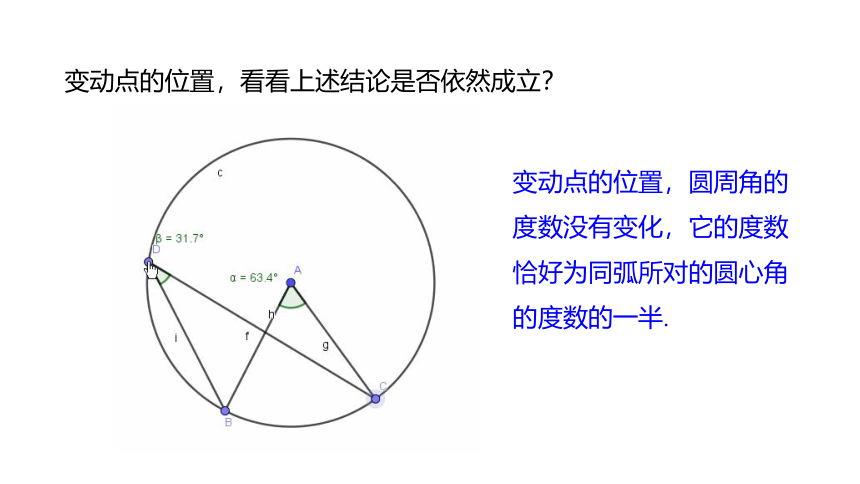
变动点的位置,看看上述结论是否依然成立?
变动点的位置,圆周角的度数没有变化,它的度数恰好为同弧所对的圆心角的度数的一半.
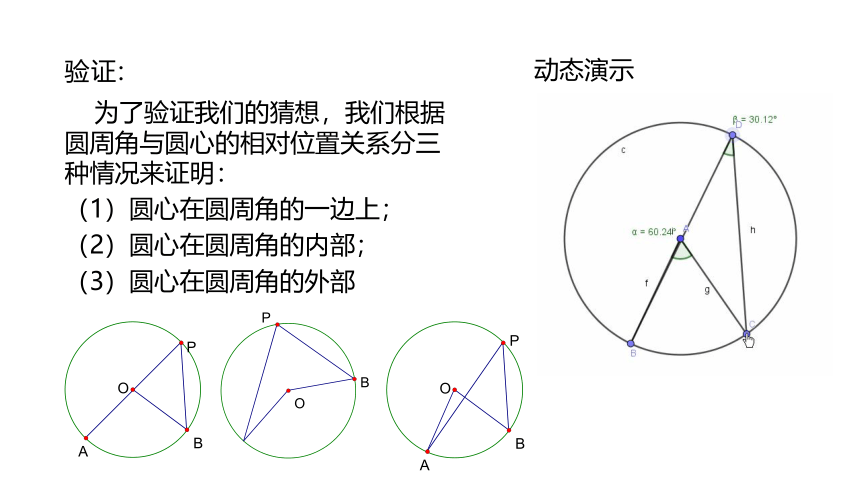
验证:
为了验证我们的猜想,我们根据圆周角与圆心的相对位置关系分三种情况来证明:
(1)圆心在圆周角的一边上;
(2)圆心在圆周角的内部;
(3)圆心在圆周角的外部
动态演示
我们先来证第(1)种情况:圆心在圆周角的一边上;
证明:∵ OB=OP,
∴∠P=∠B.
∵∠AOB是△OBP的外角,
∴∠P=∠AOB.
证明第(2)情况:圆心在圆周角的内部;
连结PO并延长交⊙于C
由(1)可知:
∠APC= ∠AOC,
∠BPC= ∠BOC,
∴ ∠APC+ ∠BPC= ( ∠AOC+ ∠BOC),
即∠APB= ∠AOB.
证明第(3)种情况:圆心在圆周角的外部
连结PO并延长交⊙O于C,
由(1)可知:
∠APC= ∠AOC,
∠BPC= ∠BOC,
∴ ∠BPC- ∠APC = ( ∠BOC- ∠AOC ),
即∠APB= ∠AOB.
圆周角的度数等于这条弧所对的圆心角度数的一半.
圆周角定理
例1 如图,∠A是圆O的圆周角,∠A=40°,求∠OBC的度数。
O
C
B
A
例题讲解
如图,∠A、∠A1、∠A2和∠A3都是弧BC所对的圆周角,那么他们相等吗?
因为∠A、∠A1、∠A2和∠A3所对弧上的圆心角均为∠BOC,由圆周角定理可知∠A=∠A1=∠A2=∠A3.
A1
A2
A3
获取新知
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
动态演示
圆周角定理的推论
例2 如图,OA,OB,OC都是⊙O的半径,∠AOB=50°,∠BOC=70°,求∠ACB和∠BAC的度数.
解:∵圆心角∠AOB与圆周角∠ACB
所对的弧为 ,
∴∠ACB = ∠AOB=25°.
同理∠BAC = ∠BOC=35°.
例题讲解
1、判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
随堂演练
2.圆周角的两个特征:
(1) ,
(2)___________________.
3.在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的_____.
顶点在圆上
两边都与圆相交
一半
4.如图1,A,B,C是⊙O上的三点,∠B=75°,则∠AOC=_____°.
150
图1
5. 如图2,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角,若∠BCD=25°,则∠AOD= .
图2
130°
O
A
B
C
D
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
第2章 圆
2.2.2 圆周角定理及其推论1
复习引入
1.什么叫圆心角
.
O
A
B
顶点在圆心的角叫圆心角
2. 圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等.
.
O
A
问题:将圆心角顶点向上移,直至与⊙O相交于点C,观察得到的∠ACB有什么特征?
C
顶点在圆上
两边都与圆相交
这样的角叫圆周角.
B
探究点一 圆周角的概念
圆周角的定义:顶点在圆上,并且两边与圆相交的角叫做圆周角.
获取新知
我们把∠ACB叫作所对圆周角, 叫作圆周角∠ACB所对的弧.
探究点二 圆周角定理
圆周角在我们生活中处处可见,比如,我们从团旗上的图案抽象出如图所示图形,图形中就有很多圆周角.
E
·
A
O
D
B
C
每位同学画一个圆,然后任意画一个圆周角,以及相应的圆心角(它所对的弧也是圆周角所对的弧),量出它们的度数,看它们之间有什么关系?
·
O
A
C
B
量出∠BAC与∠BOC的度数,它们有什么关系?
∠BAC= ∠BOC
与同桌或邻近桌的同学交流,猜测一条弧所对的圆周角与圆心角有什么关系.你能证明这个猜测吗?
猜测:同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半.
变动点的位置,看看上述结论是否依然成立?
变动点的位置,圆周角的度数没有变化,它的度数恰好为同弧所对的圆心角的度数的一半.
验证:
为了验证我们的猜想,我们根据圆周角与圆心的相对位置关系分三种情况来证明:
(1)圆心在圆周角的一边上;
(2)圆心在圆周角的内部;
(3)圆心在圆周角的外部
动态演示
我们先来证第(1)种情况:圆心在圆周角的一边上;
证明:∵ OB=OP,
∴∠P=∠B.
∵∠AOB是△OBP的外角,
∴∠P=∠AOB.
证明第(2)情况:圆心在圆周角的内部;
连结PO并延长交⊙于C
由(1)可知:
∠APC= ∠AOC,
∠BPC= ∠BOC,
∴ ∠APC+ ∠BPC= ( ∠AOC+ ∠BOC),
即∠APB= ∠AOB.
证明第(3)种情况:圆心在圆周角的外部
连结PO并延长交⊙O于C,
由(1)可知:
∠APC= ∠AOC,
∠BPC= ∠BOC,
∴ ∠BPC- ∠APC = ( ∠BOC- ∠AOC ),
即∠APB= ∠AOB.
圆周角的度数等于这条弧所对的圆心角度数的一半.
圆周角定理
例1 如图,∠A是圆O的圆周角,∠A=40°,求∠OBC的度数。
O
C
B
A
例题讲解
如图,∠A、∠A1、∠A2和∠A3都是弧BC所对的圆周角,那么他们相等吗?
因为∠A、∠A1、∠A2和∠A3所对弧上的圆心角均为∠BOC,由圆周角定理可知∠A=∠A1=∠A2=∠A3.
A1
A2
A3
获取新知
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
动态演示
圆周角定理的推论
例2 如图,OA,OB,OC都是⊙O的半径,∠AOB=50°,∠BOC=70°,求∠ACB和∠BAC的度数.
解:∵圆心角∠AOB与圆周角∠ACB
所对的弧为 ,
∴∠ACB = ∠AOB=25°.
同理∠BAC = ∠BOC=35°.
例题讲解
1、判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
随堂演练
2.圆周角的两个特征:
(1) ,
(2)___________________.
3.在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的_____.
顶点在圆上
两边都与圆相交
一半
4.如图1,A,B,C是⊙O上的三点,∠B=75°,则∠AOC=_____°.
150
图1
5. 如图2,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角,若∠BCD=25°,则∠AOD= .
图2
130°
O
A
B
C
D
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
