湘教版数学九年级下册2.1 圆的对称性 同步课件(共19张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.1 圆的对称性 同步课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:42:04 | ||
图片预览


文档简介
(共19张PPT)
2.1 圆的对称性
第2章 圆
情景引入
生活剪影
获取新知
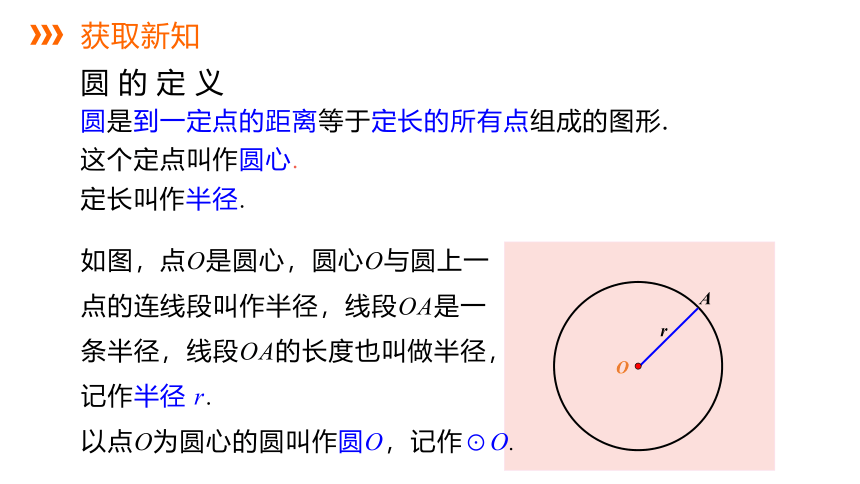
圆是到一定点的距离等于定长的所有点组成的图形.
·
定长叫作半径.
这个定点叫作圆心.
O
A
圆的定义
如图,点O是圆心,圆心O与圆上一点的连线段叫作半径,线段OA是一条半径,线段OA的长度也叫做半径,记作半径 r.
以点O为圆心的圆叫作圆O,记作⊙O.
r
·
O
r
A
圆心
半径
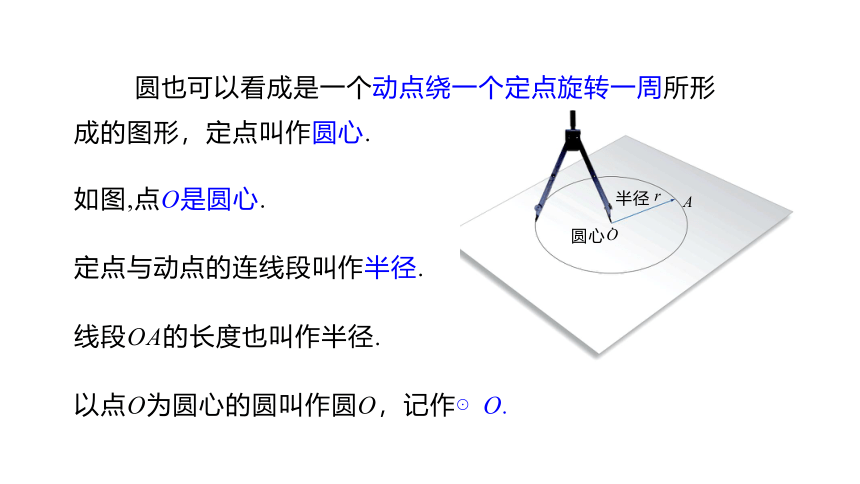
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O.
定点与动点的连线段叫作半径.
线段OA的长度也叫作半径.
如图,点O是圆心.
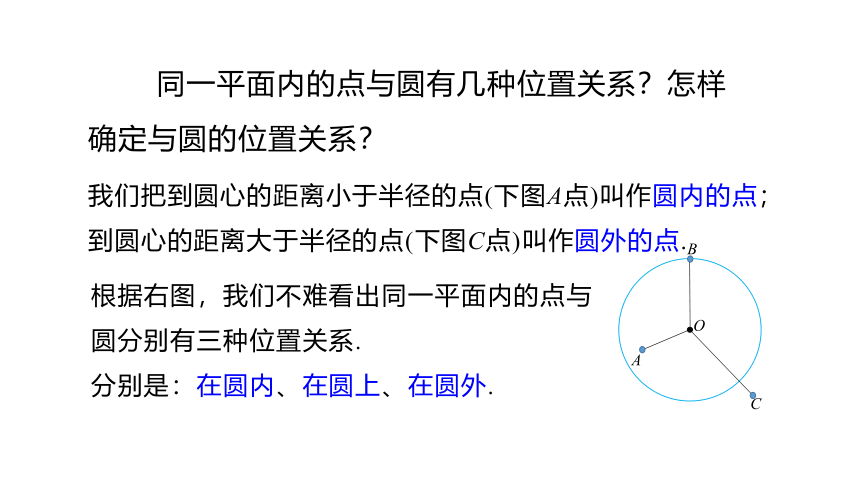
同一平面内的点与圆有几种位置关系?怎样确定与圆的位置关系?
我们把到圆心的距离小于半径的点(下图A点)叫作圆内的点;
到圆心的距离大于半径的点(下图C点)叫作圆外的点.
根据右图,我们不难看出同一平面内的点与圆分别有三种位置关系.
分别是:在圆内、在圆上、在圆外.
O
A
B
C
r
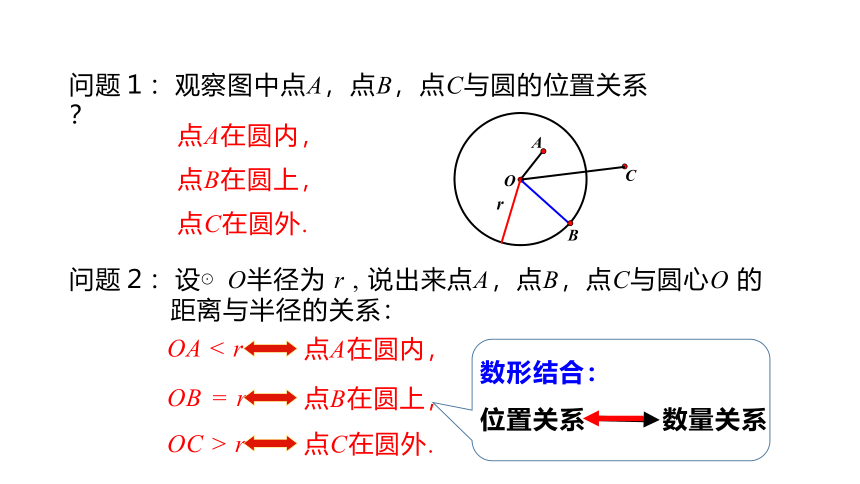
问题2:设⊙O半径为 r , 说出来点A,点B,点C与圆心O 的距离与半径的关系:
·
C
O
A
B
OC > r
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r
OB = r
点A在圆内,
点B在圆上,
点C在圆外.
数形结合:
位置关系
数量关系
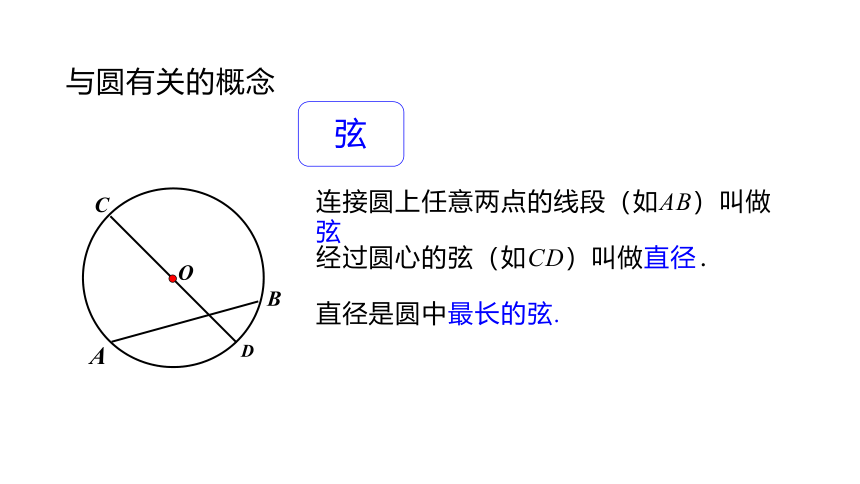
经过圆心的弦(如CD)叫做直径.
连接圆上任意两点的线段(如AB)叫做弦
·
B
O
A
C
与圆有关的概念
D
弦
直径是圆中最长的弦.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。
·
C
O
A
B
弧
1. 用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
这两个圆
重合
探究
2. 现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?这体现圆具有什么样的性质?
圆是旋转对称图形,即圆绕圆心旋转任意角度,都能与自身重合。特别地,圆是中心对称图形,圆心是它的对称中心.
·
能够重合的两个圆叫作相等的圆,或等圆。能够互相重合的弧叫做等弧。
探究
例1 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明: ∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
例题讲解
例2 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:已知⊙A的半径r=3 cm.
(1) 因为 ,所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r, 所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.
在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
获取新知
直径CD两侧的两个半圆能够完全重合.
这体现圆具有什么样的对称性?
圆是轴对称图形,
任意一条直径所在的直线,都是圆的对称轴.
圆的对称性
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
可利用折叠的方法即可体现上述问题.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可体现这个问题.
如图,为什么通常要把车轮设计成圆形? 请说说理由.
因为圆心到圆上各个点的距离相等,都等于半径,车轴离开地面的距离始终等于半径,车子就可以达到平稳的行驶;相同的面积时,圆的周长最长,节省材料;变滑动摩擦为滚动摩擦,省力;等,……
议一议
.
O
A
C
P
H
G
F
E
1、看图填空:
(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
D
B
Q
随堂演练
2.判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(7)圆心相同,半径相等的两个圆是同心圆;
(8)半径相等的两个圆是等圆.
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
√
×
×
×
×
√
×
√
3.已知⊙O的直径为10 cm,点P不在⊙O外,则OP的长( )
A.小于5 cm B.不大于5 cm
C.小于10 cm D.不大于10 cm
B
课堂小结
1.回顾圆的两种定义,弦(直径),弧(半圆、优弧、劣弧、等弧),等圆等知识点.
2.通过这节课的学习,你掌握了哪些新知识,还有哪些疑问 请与同伴交流.
2.1 圆的对称性
第2章 圆
情景引入
生活剪影
获取新知
圆是到一定点的距离等于定长的所有点组成的图形.
·
定长叫作半径.
这个定点叫作圆心.
O
A
圆的定义
如图,点O是圆心,圆心O与圆上一点的连线段叫作半径,线段OA是一条半径,线段OA的长度也叫做半径,记作半径 r.
以点O为圆心的圆叫作圆O,记作⊙O.
r
·
O
r
A
圆心
半径
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O.
定点与动点的连线段叫作半径.
线段OA的长度也叫作半径.
如图,点O是圆心.
同一平面内的点与圆有几种位置关系?怎样确定与圆的位置关系?
我们把到圆心的距离小于半径的点(下图A点)叫作圆内的点;
到圆心的距离大于半径的点(下图C点)叫作圆外的点.
根据右图,我们不难看出同一平面内的点与圆分别有三种位置关系.
分别是:在圆内、在圆上、在圆外.
O
A
B
C
r
问题2:设⊙O半径为 r , 说出来点A,点B,点C与圆心O 的距离与半径的关系:
·
C
O
A
B
OC > r
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r
OB = r
点A在圆内,
点B在圆上,
点C在圆外.
数形结合:
位置关系
数量关系
经过圆心的弦(如CD)叫做直径.
连接圆上任意两点的线段(如AB)叫做弦
·
B
O
A
C
与圆有关的概念
D
弦
直径是圆中最长的弦.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。
·
C
O
A
B
弧
1. 用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
这两个圆
重合
探究
2. 现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?这体现圆具有什么样的性质?
圆是旋转对称图形,即圆绕圆心旋转任意角度,都能与自身重合。特别地,圆是中心对称图形,圆心是它的对称中心.
·
能够重合的两个圆叫作相等的圆,或等圆。能够互相重合的弧叫做等弧。
探究
例1 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明: ∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
例题讲解
例2 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:已知⊙A的半径r=3 cm.
(1) 因为 ,所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r, 所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.
在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
获取新知
直径CD两侧的两个半圆能够完全重合.
这体现圆具有什么样的对称性?
圆是轴对称图形,
任意一条直径所在的直线,都是圆的对称轴.
圆的对称性
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
可利用折叠的方法即可体现上述问题.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可体现这个问题.
如图,为什么通常要把车轮设计成圆形? 请说说理由.
因为圆心到圆上各个点的距离相等,都等于半径,车轴离开地面的距离始终等于半径,车子就可以达到平稳的行驶;相同的面积时,圆的周长最长,节省材料;变滑动摩擦为滚动摩擦,省力;等,……
议一议
.
O
A
C
P
H
G
F
E
1、看图填空:
(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
D
B
Q
随堂演练
2.判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(7)圆心相同,半径相等的两个圆是同心圆;
(8)半径相等的两个圆是等圆.
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
√
×
×
×
×
√
×
√
3.已知⊙O的直径为10 cm,点P不在⊙O外,则OP的长( )
A.小于5 cm B.不大于5 cm
C.小于10 cm D.不大于10 cm
B
课堂小结
1.回顾圆的两种定义,弦(直径),弧(半圆、优弧、劣弧、等弧),等圆等知识点.
2.通过这节课的学习,你掌握了哪些新知识,还有哪些疑问 请与同伴交流.
