2022--2023学年沪科版九年级数学上册21.5.3 k的几何意义 课件 (共19张PPT)
文档属性
| 名称 | 2022--2023学年沪科版九年级数学上册21.5.3 k的几何意义 课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 706.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:49:30 | ||
图片预览






文档简介
(共19张PPT)
课题导入
课题导入
|k|越小,越接近坐标原点
21.5.3 k的几何意义
1、理解反比例函数中“k”的几何意义;
2、体会数形结合思想的应用.
目标引领
独立自学
如图,是 的图象,点P是图象上的一个动点.
(1)若P(1,y),则四边形OABC的面积=_____
(2)若P(3,y),则四边形OAPB的面积= .
(3)若P(5,y),则四边形OAPB的面积=_____
想一想:若P(x,y),
则四边形OAPB的面积= .
6
6
6
6
x
0
B
A
P(1,y)
P(3,y)
P(5,y)
A
A
B
B
y
思考:
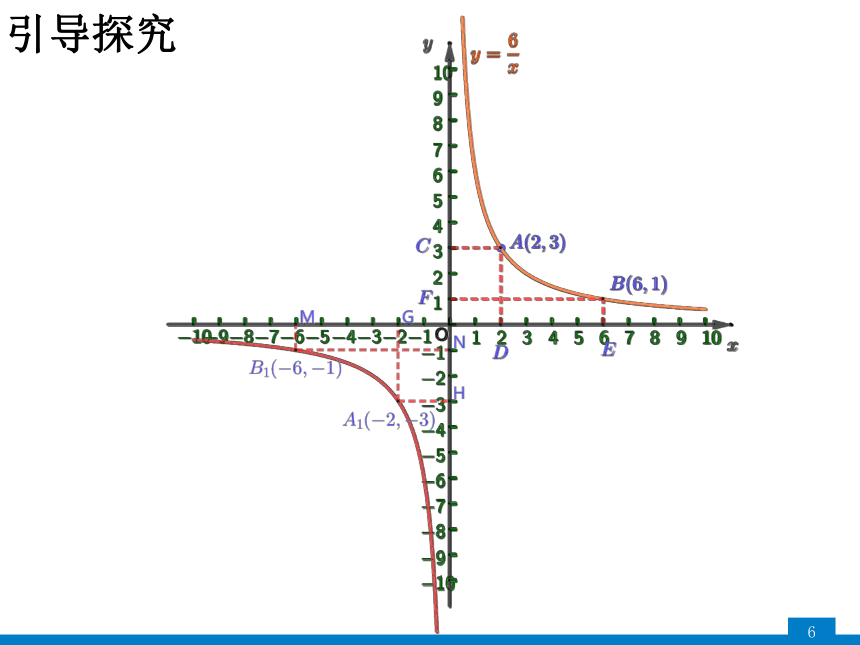
引导探究
3分钟后!
引导探究
从双曲线上任意一点向x、y轴分别作垂线段,两条垂线段与两坐标轴所围成的长方形的面积=︱k︱.
引导探究
k的几何意义
1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D,PF⊥y轴于F.则矩形ODPF的面积为 .
2
P
D
o
y
x
引导探究
F
已知解析式求面积
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .
引导探究
已知面积求解析式(注意正负)
x
y
O
A
3.如图A、B在 上,过A、B两点分别向y轴、x轴作垂线段,设四边形ACEG、BGDF的面积分别是S、S',若阴影部分的面积是1,则S+S'=_______
B
F
D
C
E
S
S'
1
4
引导探究
G
P
D
o
y
x
4.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
(m,n)
1
引导探究
P(m,n)
A
o
y
x
过P作x轴的垂线,垂足为A,则它与坐标轴
形成的三角形的面积是不变的,为:
推广:反比例函数与三角形面积
5.如图A在 上,AB⊥x轴,
且△AOB的面积是2,则k= .
x
y
O
-4
引导探究
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
引导探究
引导探究
引导探究
变式:如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线, 垂足分别为D、C,若矩形ABCD的面积是8,则k的值为 .
E
12
引导探究
目标升华
你有什么收获或疑惑?
当堂诊学
1.如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,点C和点D在x轴上,若四边形ABCD为矩形,则矩形ABCD的面积为 .
2
2.如图,直线l⊥x轴于点P,且与反比例函数 及
的图象分别交于A、B两点,连接OA、OB,已知
△OAB的面积为4,则k1-k2=_____.
8
强化补清
完成课后习题
课题导入
课题导入
|k|越小,越接近坐标原点
21.5.3 k的几何意义
1、理解反比例函数中“k”的几何意义;
2、体会数形结合思想的应用.
目标引领
独立自学
如图,是 的图象,点P是图象上的一个动点.
(1)若P(1,y),则四边形OABC的面积=_____
(2)若P(3,y),则四边形OAPB的面积= .
(3)若P(5,y),则四边形OAPB的面积=_____
想一想:若P(x,y),
则四边形OAPB的面积= .
6
6
6
6
x
0
B
A
P(1,y)
P(3,y)
P(5,y)
A
A
B
B
y
思考:
引导探究
3分钟后!
引导探究
从双曲线上任意一点向x、y轴分别作垂线段,两条垂线段与两坐标轴所围成的长方形的面积=︱k︱.
引导探究
k的几何意义
1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D,PF⊥y轴于F.则矩形ODPF的面积为 .
2
P
D
o
y
x
引导探究
F
已知解析式求面积
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .
引导探究
已知面积求解析式(注意正负)
x
y
O
A
3.如图A、B在 上,过A、B两点分别向y轴、x轴作垂线段,设四边形ACEG、BGDF的面积分别是S、S',若阴影部分的面积是1,则S+S'=_______
B
F
D
C
E
S
S'
1
4
引导探究
G
P
D
o
y
x
4.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
(m,n)
1
引导探究
P(m,n)
A
o
y
x
过P作x轴的垂线,垂足为A,则它与坐标轴
形成的三角形的面积是不变的,为:
推广:反比例函数与三角形面积
5.如图A在 上,AB⊥x轴,
且△AOB的面积是2,则k= .
x
y
O
-4
引导探究
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
引导探究
引导探究
引导探究
变式:如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线, 垂足分别为D、C,若矩形ABCD的面积是8,则k的值为 .
E
12
引导探究
目标升华
你有什么收获或疑惑?
当堂诊学
1.如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,点C和点D在x轴上,若四边形ABCD为矩形,则矩形ABCD的面积为 .
2
2.如图,直线l⊥x轴于点P,且与反比例函数 及
的图象分别交于A、B两点,连接OA、OB,已知
△OAB的面积为4,则k1-k2=_____.
8
强化补清
完成课后习题
