2022--2023学年沪科版九年级数学上册22.1.2 比例线段 课件 (共16张PPT)
文档属性
| 名称 | 2022--2023学年沪科版九年级数学上册22.1.2 比例线段 课件 (共16张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 165.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:51:48 | ||
图片预览





文档简介
(共16张PPT)
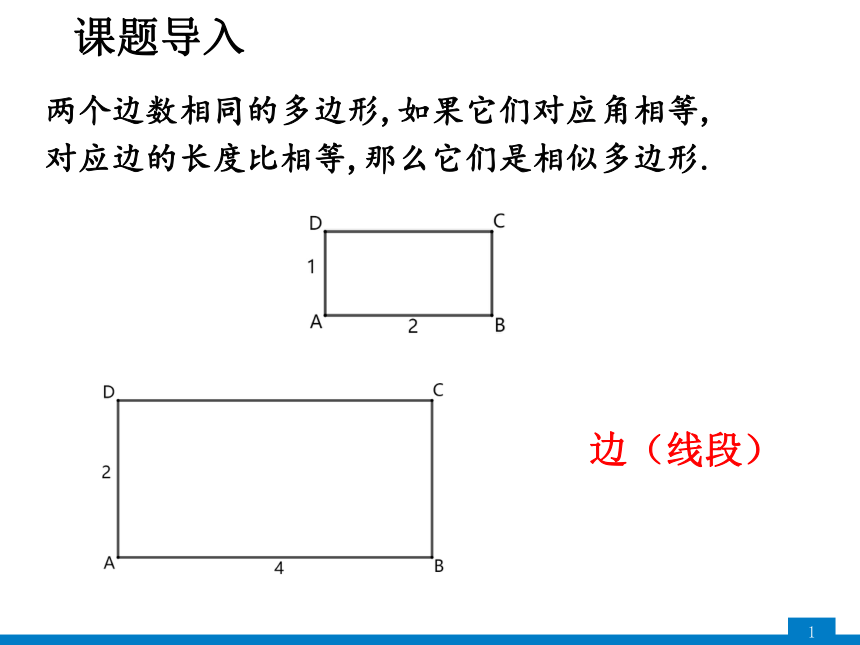
课题导入
两个边数相同的多边形,如果它们对应角相等,
对应边的长度比相等,那么它们是相似多边形.
边(线段)
22.1.2 比例线段
课题导入
1.知道线段的比的概念,会计算两条线段的比;
2.理解成比例线段的概念;
3.掌握成比例线段的判定方法.
目标引领
认真阅读课本p65页到p66页,思考下面问题:
1.什么是两条线段的比?
2.根据以上理解填空:
限时5分钟,看谁又快又好!
独立自学
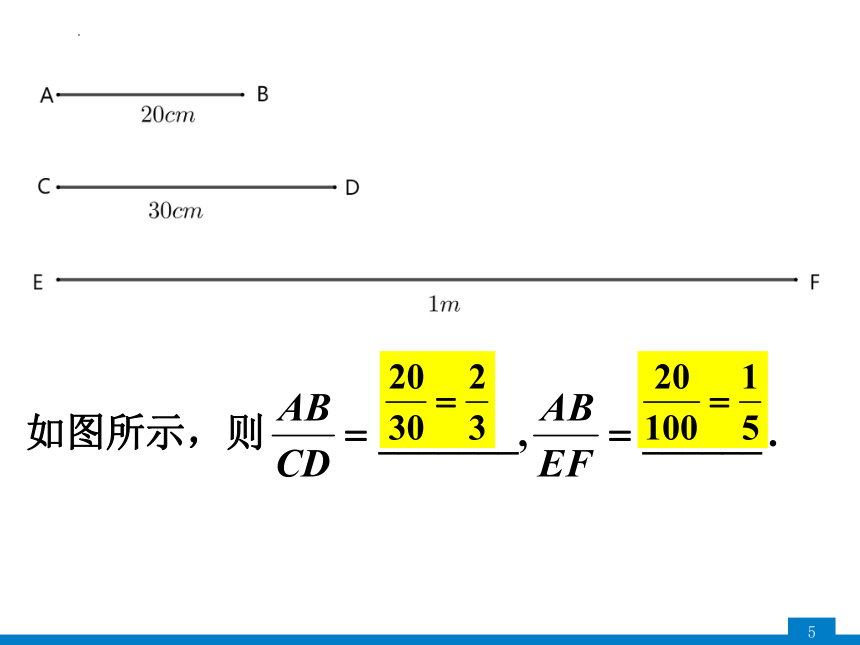
(1)若线段AB=6cm,CD=4cm,则 .
(2)若线段AB=8cm,CD=2dm,则 .
两条线段的比
用 去度量两条线段a、b,得到它们的长度,把这两条 叫做这两条线段的比,
记做:
同一个长度单位
线段长度的比
注意:
(1)单位要统一;
(2)两条线段的比值是一个没有单位的正数;
(3)明确两条线段的先后顺序.
引导探究
1.在比例尺为1:2000的地图上,有相距3.5cm的A、B
两地,则A、B两地间的实际距离为 .
7000cm
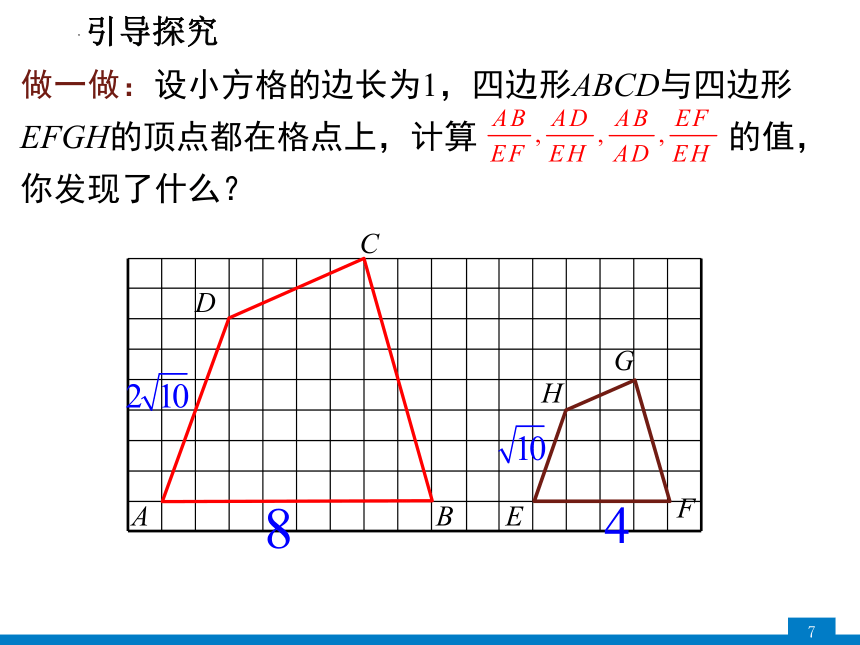
做一做:设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,计算 的值,
你发现了什么?
A
B
C
D
G
H
E
F
引导探究
四条线段a, b, c, d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a , b ,c , d叫作成比例线段,简称比例线段.
AB,EF,AD,EH是成比例线段,
AB,AD,EF,EH也是成比例线段.
注意:四条线段成比例时要注意它们的排列顺序!
引导探究
成比例线段
如果
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
a、d 叫做比例外项,
b、c 叫做比例内项,
d 叫做 a、b、c的第四比例项.
相关概念
引导探究
2.已知a、b、c、d是成比例线段,其中a=3cm,
b=2cm,c=6cm,则线段d= .
4cm
3.(1)若c是a、b的比例中项,且a=2,b=8,则c= ;
(2)若线段c是线段a、b的比例中项,且a=2, b=8,则c= ;
方法指导:注意区分线段的比例中项与数字的比例
中项的区别
4
引导探究
特殊情况:若作为比例内项的两条线段相等,即a:b=b:c,则b叫做a,c的比例中项.
变式:若b:c=3:2,且c是b和a的比例中项,
则a:c的值是 .
2:3
4.已知:线段a=3,b=8,c=6,d=4.则
(1)线段a、b、c、d是否成比例?
(2)线段a、d、c、b是否成比例?
引导探究
判断a:b= c:d
a:d= c:b
变式:判断下列四条线段是否是成比例线段.
一般将线段按大小顺序排列,看前两条线段的长度比是否等于后两条线段长度比.
给定顺序
重组顺序
5.已知三条线段的长度分别是2,3,4,如果再添上一条线段,使之能与已知的三条线段组成比例式,这条线段的长度是多少
引导探究
解:设这个数为x.
(1)当x为最小数时:
(2)当x为最大数时:
(3)当x为中间数时:
解这三个方程可得x= 或 或6.
或
4x=2 3
2x=3 4
3x=2 4
6.如图,一块矩形绸布的长AB=am,AD=1m,按照图中所示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的长与宽的比与原绸布的长与宽的比相同,即 ,那么a的值应当是多少?
引导探究
本节课你有哪些收获和疑惑?
目标升华
4.若x是a、b的比例中项,且a=3,b=27, 则x= ;若线段x是线段a、b的比例中项,且a=3,b=27,则x= ;
1.在比例尺为1:200的地图上,测得A、B两地间的图上
距离为4.5cm,则A、B两地间的实际距离为 .
当堂诊学
校本配套作业
强化补清
课题导入
两个边数相同的多边形,如果它们对应角相等,
对应边的长度比相等,那么它们是相似多边形.
边(线段)
22.1.2 比例线段
课题导入
1.知道线段的比的概念,会计算两条线段的比;
2.理解成比例线段的概念;
3.掌握成比例线段的判定方法.
目标引领
认真阅读课本p65页到p66页,思考下面问题:
1.什么是两条线段的比?
2.根据以上理解填空:
限时5分钟,看谁又快又好!
独立自学
(1)若线段AB=6cm,CD=4cm,则 .
(2)若线段AB=8cm,CD=2dm,则 .
两条线段的比
用 去度量两条线段a、b,得到它们的长度,把这两条 叫做这两条线段的比,
记做:
同一个长度单位
线段长度的比
注意:
(1)单位要统一;
(2)两条线段的比值是一个没有单位的正数;
(3)明确两条线段的先后顺序.
引导探究
1.在比例尺为1:2000的地图上,有相距3.5cm的A、B
两地,则A、B两地间的实际距离为 .
7000cm
做一做:设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,计算 的值,
你发现了什么?
A
B
C
D
G
H
E
F
引导探究
四条线段a, b, c, d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a , b ,c , d叫作成比例线段,简称比例线段.
AB,EF,AD,EH是成比例线段,
AB,AD,EF,EH也是成比例线段.
注意:四条线段成比例时要注意它们的排列顺序!
引导探究
成比例线段
如果
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
a、d 叫做比例外项,
b、c 叫做比例内项,
d 叫做 a、b、c的第四比例项.
相关概念
引导探究
2.已知a、b、c、d是成比例线段,其中a=3cm,
b=2cm,c=6cm,则线段d= .
4cm
3.(1)若c是a、b的比例中项,且a=2,b=8,则c= ;
(2)若线段c是线段a、b的比例中项,且a=2, b=8,则c= ;
方法指导:注意区分线段的比例中项与数字的比例
中项的区别
4
引导探究
特殊情况:若作为比例内项的两条线段相等,即a:b=b:c,则b叫做a,c的比例中项.
变式:若b:c=3:2,且c是b和a的比例中项,
则a:c的值是 .
2:3
4.已知:线段a=3,b=8,c=6,d=4.则
(1)线段a、b、c、d是否成比例?
(2)线段a、d、c、b是否成比例?
引导探究
判断a:b= c:d
a:d= c:b
变式:判断下列四条线段是否是成比例线段.
一般将线段按大小顺序排列,看前两条线段的长度比是否等于后两条线段长度比.
给定顺序
重组顺序
5.已知三条线段的长度分别是2,3,4,如果再添上一条线段,使之能与已知的三条线段组成比例式,这条线段的长度是多少
引导探究
解:设这个数为x.
(1)当x为最小数时:
(2)当x为最大数时:
(3)当x为中间数时:
解这三个方程可得x= 或 或6.
或
4x=2 3
2x=3 4
3x=2 4
6.如图,一块矩形绸布的长AB=am,AD=1m,按照图中所示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的长与宽的比与原绸布的长与宽的比相同,即 ,那么a的值应当是多少?
引导探究
本节课你有哪些收获和疑惑?
目标升华
4.若x是a、b的比例中项,且a=3,b=27, 则x= ;若线段x是线段a、b的比例中项,且a=3,b=27,则x= ;
1.在比例尺为1:200的地图上,测得A、B两地间的图上
距离为4.5cm,则A、B两地间的实际距离为 .
当堂诊学
校本配套作业
强化补清
