人教版2022--2023九年级(上)数学第二十一单元质量检测试卷A(含解析)
文档属性
| 名称 | 人教版2022--2023九年级(上)数学第二十一单元质量检测试卷A(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2022-20203学年九年级(上)第二十一章一元二次方程检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 根据下列表格的对应值:
判断方程 (,,, 为常数)的一个解 的取值范围是
A. B. C. D.
2. 关于 的方程 的两个根是 和 ,则 因式分解的结果是
A. B.
C. D.
3. 关于 的一元二次方程 有两个不等的整数根, 为整数,那么 的值是
A. B. C. D.
4. 【摸底测试 】
方程 的两个根为
A. , B. ,
C. , D. ,
5. 游行队伍有 行 列,后又增加了 人,且队伍增加的行、列数相同,设增加的行、列数为 ,下列方程符合题意的是
A.
B.
C.
D.
6. 【摸底测试 】
方程 的根是
A. , B. ,
C. , D. ,
7. 如图是某月的日历表,在此日历表上用一个矩形圈出三行三列的 个数(如 ,,,,,,,,).若圈出的 个数中,最大数与最小数的积为 ,则这 个数的和为
A. B. C. D.
8. 某企业 年初投资 万元生产适销对路产品, 年底将获得的利润与年初的投资的和作为 年初的投资,到 年底,两年共获利润 万元.已知 年的年获利率比 年的获利率多 个百分点.如果设 年的获利率是 ,那么下列所列出的方程中正确的是
A. B.
C. D.
9. 关于 的一元二次方程 的一个根是 ,则 的值是
A. 或 B. C. D.
10. 关于 的方程 的一个实数根的倒数恰是它本身,则 的值是
A. B. C. 或 D.
二、填空题(共6小题;每小题3分,共18分)
11. 快过元旦了,全班同学每两人互发一条祝福短信,共发了 条,设全班有 名同学,则可列方程为 .
12. 方程 的解是 .
13. 某数的正平方根比它的倒数的正平方根的 倍多 ,求这个数.若设这个数为 ,列出方程是 .
14. 已知方程 和 有共同的根 ,则 , .
15. 下列四个方程:① ;② ;③ ;④ .其中,无理方程是 (只要填写方程的序号).
16. 网上流行一个游戏,发起游戏的人首先发出一个“祝福”链接,将这个“祝福”链接发给 个人,收到链接的人也需把链接发给相同数量的新人,经过两轮传播后,共有 人参与了这个“祝福”链接的传播,则 的值为 .
三、解答题(共9小题;共72分)
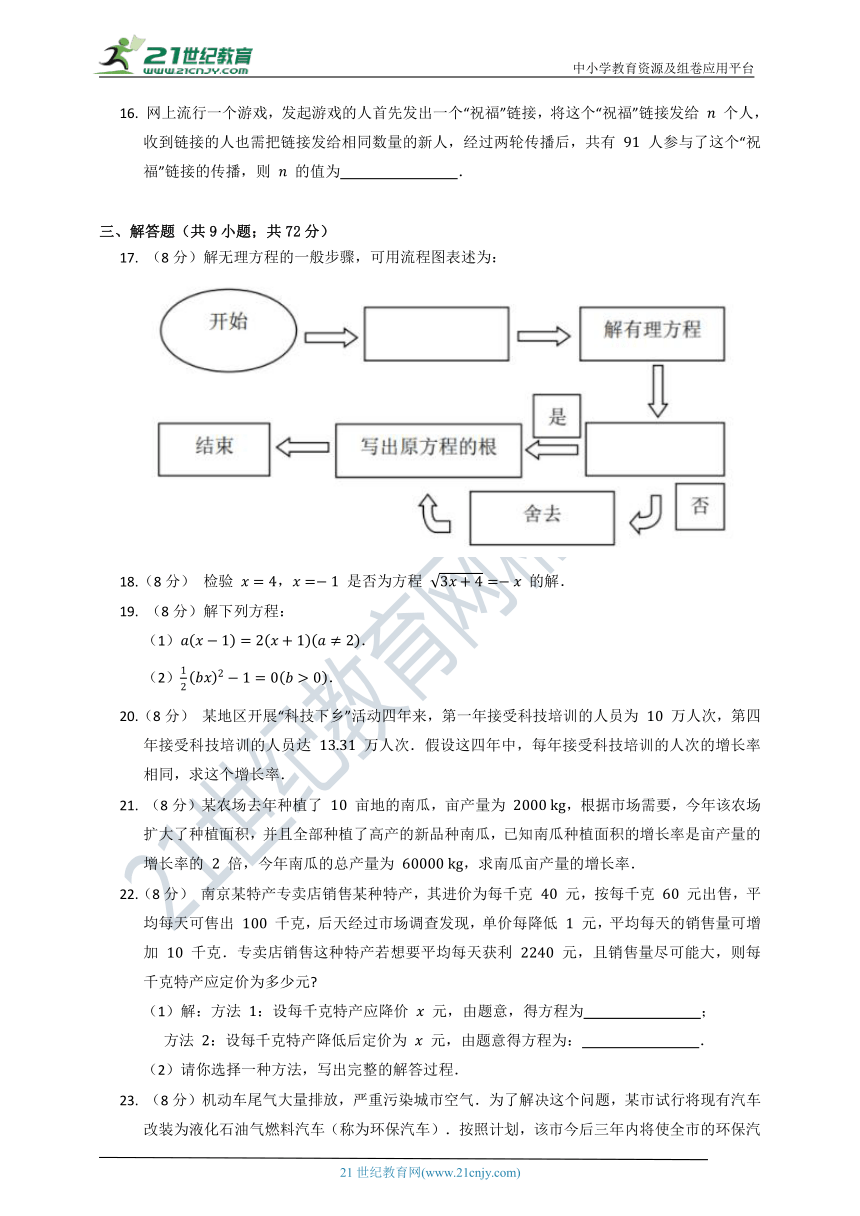
17. (8分)解无理方程的一般步骤,可用流程图表述为:
18.(8分) 检验 , 是否为方程 的解.
19. (8分)解下列方程:
(1).
(2).
20.(8分) 某地区开展“科技下乡”活动四年来,第一年接受科技培训的人员为 万人次,第四年接受科技培训的人员达 万人次.假设这四年中,每年接受科技培训的人次的增长率相同,求这个增长率.
21. (8分)某农场去年种植了 亩地的南瓜,亩产量为 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的 倍,今年南瓜的总产量为 ,求南瓜亩产量的增长率.
22.(8分) 南京某特产专卖店销售某种特产,其进价为每千克 元,按每千克 元出售,平均每天可售出 千克,后天经过市场调查发现,单价每降低 元,平均每天的销售量可增加 千克.专卖店销售这种特产若想要平均每天获利 元,且销售量尽可能大,则每千克特产应定价为多少元
(1)解:方法 :设每千克特产应降价 元,由题意,得方程为 ;
方法 :设每千克特产降低后定价为 元,由题意得方程为: .
(2)请你选择一种方法,写出完整的解答过程.
23. (8分)机动车尾气大量排放,严重污染城市空气.为了解决这个问题,某市试行将现有汽车改装为液化石油气燃料汽车(称为环保汽车).按照计划,该市今后三年内将使全市的环保汽车由今年的 辆增加到 辆,假如今后三年内这种环保汽车每年增长的百分率相同,求这个百分率.
24. (8分)分解因式:
(1).
(2).
25. (8分)实验与探究:三角点阵前 行的点数计算.
如图是一个三角点阵,从上向下数有无数多行,其中第一行有 个点,第二行有 个点 第 行有 个点 容易发现, 是三角点阵中前 行的点数的和,你能发现 是前多少行的点数的和吗
如果要用试验的方法,由上而下地逐行的相加其点数,虽然你能发现 .得知 是前 行的点数的和,但是这样寻找答案需我们先探求三角点阵中前 行的点数的和与 的数量关系是 ,可以发现.
把两个中括号中的第一项相加,第二项相加 第 项相加,上式等号的后边变形为这 个小括号都等于 ,整个式子等于 ,于是得到 ,
这就是说,三角点阵中前 项的点数的和是 .
下列用一元二次方程解决上述问题:
设三角点阵中前 行的点数的和为 ,则有 整理这个方程,得 ,
解方程得 ,.
根据问题中未知数的意义确定 ,即三角点阵中前 行的点数的和是 .
请你根据上述材料回答下列问题:
(1)三角点阵中前 行的点数的和能是 吗 如果能,求出 ;如果不能,试用一元二次方程说明道理.
(2)如果把图中的三角点阵中各行的点数依次换成 ,,,,,,你能探究出前 行的点数的和满足什么规律吗 这个三角点阵中前 行的点数的和能是 吗 如果能,求出 ;如果不能,试用一元二次方程说明道理.
答案
第一部分
1. C
2. B
3. A
【解析】 ,即 ,
解得: , .
关于 的一元二次方程 有两个不等的整数根,
, 为整数,且 .
又 为整数,
.
4. D
【解析】,
,
或 ,
,,
故选:D.
5. B
【解析】依题意,得 .
故选B.
6. B
【解析】,
,
或 ,
解得 ,,
故选:B.
7. D
【解析】根据题意可以得出,圈出的 个数中,最大数与最小数的差为 ,设最小数为 ,则最大数为 ,所以 ,解得 ,(不合题意,舍去),故圈出的 个数中,第一行的三个数为 ,,,第二行的三个数为 ,,,第三行的三个数为 ,,,故这 个数的和为 .
8. A
9. B
【解析】 方程 ,
,
.
将 代入 ,得:,
解得:(不合题意,舍去),.
10. C
【解析】倒数等于它本身的数是 ,即原方程的一个根为 或 .把 代入原方程得 ,解得 ;把 代入原方程得 ,解得 .
第二部分
11.
【解析】该班级共有 名同学,则每个人要发 条短信,
根据题意可得等量关系:
人数 每个人所发的短信数量 总短信数量,
故可列方程为 .
12.
13.
14. ,
15. ①
16.
【解析】由题意得 ,解得 ,(舍去),
的值为 .
第三部分
17. 去根号;检验
18. 不是方程的解, 是方程的解.
19. (1) ;
(2) .
20. .
提示:设这四年中,每年接受科技培训的人次的增长率是 ,根据题意可列方程:.
21. 设南瓜亩产量的增长率为 ,则种植面积的增长率为 .
根据题意,得:
解这个方程,得
答:南瓜亩产量的增长率为 .
22. (1) ;
【解析】方法 :设每千克特产应降价 元.
根据题意,得 .
方法 :设每千克特产降价后定价为 元,
由题意,得 ,
故答案为:,;
(2) 见解析
【解析】设每千克特产应降价 元.
根据题意,得 ,
解得 ,.
要让销售量尽可能大,只能取 ,
元,
答:每千克特产应定价 元.
23. 设今后三年内这种环保型汽车每年增长的百分率是 ,
根据题意可列方程:
解得:
答:今后三年内这种环保型汽车每年增长的百分率是 .
24. (1) .
(2) .
25. (1) 由题意可得 ,
整理得 ,
此方程无正整数解,
所以,三角点阵中前 行的点数的和不可能是 .
(2) 由题意可得 ;
依题意,得 ,
整理得 , ,
, ,
为正整数,
.
故 的值是 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2022-20203学年九年级(上)第二十一章一元二次方程检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 根据下列表格的对应值:
判断方程 (,,, 为常数)的一个解 的取值范围是
A. B. C. D.
2. 关于 的方程 的两个根是 和 ,则 因式分解的结果是
A. B.
C. D.
3. 关于 的一元二次方程 有两个不等的整数根, 为整数,那么 的值是
A. B. C. D.
4. 【摸底测试 】
方程 的两个根为
A. , B. ,
C. , D. ,
5. 游行队伍有 行 列,后又增加了 人,且队伍增加的行、列数相同,设增加的行、列数为 ,下列方程符合题意的是
A.
B.
C.
D.
6. 【摸底测试 】
方程 的根是
A. , B. ,
C. , D. ,
7. 如图是某月的日历表,在此日历表上用一个矩形圈出三行三列的 个数(如 ,,,,,,,,).若圈出的 个数中,最大数与最小数的积为 ,则这 个数的和为
A. B. C. D.
8. 某企业 年初投资 万元生产适销对路产品, 年底将获得的利润与年初的投资的和作为 年初的投资,到 年底,两年共获利润 万元.已知 年的年获利率比 年的获利率多 个百分点.如果设 年的获利率是 ,那么下列所列出的方程中正确的是
A. B.
C. D.
9. 关于 的一元二次方程 的一个根是 ,则 的值是
A. 或 B. C. D.
10. 关于 的方程 的一个实数根的倒数恰是它本身,则 的值是
A. B. C. 或 D.
二、填空题(共6小题;每小题3分,共18分)
11. 快过元旦了,全班同学每两人互发一条祝福短信,共发了 条,设全班有 名同学,则可列方程为 .
12. 方程 的解是 .
13. 某数的正平方根比它的倒数的正平方根的 倍多 ,求这个数.若设这个数为 ,列出方程是 .
14. 已知方程 和 有共同的根 ,则 , .
15. 下列四个方程:① ;② ;③ ;④ .其中,无理方程是 (只要填写方程的序号).
16. 网上流行一个游戏,发起游戏的人首先发出一个“祝福”链接,将这个“祝福”链接发给 个人,收到链接的人也需把链接发给相同数量的新人,经过两轮传播后,共有 人参与了这个“祝福”链接的传播,则 的值为 .
三、解答题(共9小题;共72分)
17. (8分)解无理方程的一般步骤,可用流程图表述为:
18.(8分) 检验 , 是否为方程 的解.
19. (8分)解下列方程:
(1).
(2).
20.(8分) 某地区开展“科技下乡”活动四年来,第一年接受科技培训的人员为 万人次,第四年接受科技培训的人员达 万人次.假设这四年中,每年接受科技培训的人次的增长率相同,求这个增长率.
21. (8分)某农场去年种植了 亩地的南瓜,亩产量为 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的 倍,今年南瓜的总产量为 ,求南瓜亩产量的增长率.
22.(8分) 南京某特产专卖店销售某种特产,其进价为每千克 元,按每千克 元出售,平均每天可售出 千克,后天经过市场调查发现,单价每降低 元,平均每天的销售量可增加 千克.专卖店销售这种特产若想要平均每天获利 元,且销售量尽可能大,则每千克特产应定价为多少元
(1)解:方法 :设每千克特产应降价 元,由题意,得方程为 ;
方法 :设每千克特产降低后定价为 元,由题意得方程为: .
(2)请你选择一种方法,写出完整的解答过程.
23. (8分)机动车尾气大量排放,严重污染城市空气.为了解决这个问题,某市试行将现有汽车改装为液化石油气燃料汽车(称为环保汽车).按照计划,该市今后三年内将使全市的环保汽车由今年的 辆增加到 辆,假如今后三年内这种环保汽车每年增长的百分率相同,求这个百分率.
24. (8分)分解因式:
(1).
(2).
25. (8分)实验与探究:三角点阵前 行的点数计算.
如图是一个三角点阵,从上向下数有无数多行,其中第一行有 个点,第二行有 个点 第 行有 个点 容易发现, 是三角点阵中前 行的点数的和,你能发现 是前多少行的点数的和吗
如果要用试验的方法,由上而下地逐行的相加其点数,虽然你能发现 .得知 是前 行的点数的和,但是这样寻找答案需我们先探求三角点阵中前 行的点数的和与 的数量关系是 ,可以发现.
把两个中括号中的第一项相加,第二项相加 第 项相加,上式等号的后边变形为这 个小括号都等于 ,整个式子等于 ,于是得到 ,
这就是说,三角点阵中前 项的点数的和是 .
下列用一元二次方程解决上述问题:
设三角点阵中前 行的点数的和为 ,则有 整理这个方程,得 ,
解方程得 ,.
根据问题中未知数的意义确定 ,即三角点阵中前 行的点数的和是 .
请你根据上述材料回答下列问题:
(1)三角点阵中前 行的点数的和能是 吗 如果能,求出 ;如果不能,试用一元二次方程说明道理.
(2)如果把图中的三角点阵中各行的点数依次换成 ,,,,,,你能探究出前 行的点数的和满足什么规律吗 这个三角点阵中前 行的点数的和能是 吗 如果能,求出 ;如果不能,试用一元二次方程说明道理.
答案
第一部分
1. C
2. B
3. A
【解析】 ,即 ,
解得: , .
关于 的一元二次方程 有两个不等的整数根,
, 为整数,且 .
又 为整数,
.
4. D
【解析】,
,
或 ,
,,
故选:D.
5. B
【解析】依题意,得 .
故选B.
6. B
【解析】,
,
或 ,
解得 ,,
故选:B.
7. D
【解析】根据题意可以得出,圈出的 个数中,最大数与最小数的差为 ,设最小数为 ,则最大数为 ,所以 ,解得 ,(不合题意,舍去),故圈出的 个数中,第一行的三个数为 ,,,第二行的三个数为 ,,,第三行的三个数为 ,,,故这 个数的和为 .
8. A
9. B
【解析】 方程 ,
,
.
将 代入 ,得:,
解得:(不合题意,舍去),.
10. C
【解析】倒数等于它本身的数是 ,即原方程的一个根为 或 .把 代入原方程得 ,解得 ;把 代入原方程得 ,解得 .
第二部分
11.
【解析】该班级共有 名同学,则每个人要发 条短信,
根据题意可得等量关系:
人数 每个人所发的短信数量 总短信数量,
故可列方程为 .
12.
13.
14. ,
15. ①
16.
【解析】由题意得 ,解得 ,(舍去),
的值为 .
第三部分
17. 去根号;检验
18. 不是方程的解, 是方程的解.
19. (1) ;
(2) .
20. .
提示:设这四年中,每年接受科技培训的人次的增长率是 ,根据题意可列方程:.
21. 设南瓜亩产量的增长率为 ,则种植面积的增长率为 .
根据题意,得:
解这个方程,得
答:南瓜亩产量的增长率为 .
22. (1) ;
【解析】方法 :设每千克特产应降价 元.
根据题意,得 .
方法 :设每千克特产降价后定价为 元,
由题意,得 ,
故答案为:,;
(2) 见解析
【解析】设每千克特产应降价 元.
根据题意,得 ,
解得 ,.
要让销售量尽可能大,只能取 ,
元,
答:每千克特产应定价 元.
23. 设今后三年内这种环保型汽车每年增长的百分率是 ,
根据题意可列方程:
解得:
答:今后三年内这种环保型汽车每年增长的百分率是 .
24. (1) .
(2) .
25. (1) 由题意可得 ,
整理得 ,
此方程无正整数解,
所以,三角点阵中前 行的点数的和不可能是 .
(2) 由题意可得 ;
依题意,得 ,
整理得 , ,
, ,
为正整数,
.
故 的值是 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
