鲁教版(五四制)七年级数学上册 第三章 勾股定理 单元测试(含解析)
文档属性
| 名称 | 鲁教版(五四制)七年级数学上册 第三章 勾股定理 单元测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 09:22:53 | ||
图片预览

文档简介
鲁教版数学七上勾股定理单元测试
(共21题)
一、选择题(共10题)
如图,在 的网格中,点 ,, 都在格点上,每个小正方形的边长为 ,则 的值为
A. B. C. D.
以下列长度的线段为边长作三角形,可以构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
如图所示,小颖利用有一个锐角是 的三角板测量一棵树的高度,已知她与树之间的水平距离 为 , 为 (即小颖的眼睛距地面的距离),那么这棵树高是
A. B. C. D.
如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为 的正六边形,则原来的纸条宽为
A. B. C. D.
如图,点 ,, 在 上,, 是 的切线,点 为切点, 的延长线交 于点 ,若 的长为 ,则 的长是
A. B. C. D.
如图, 是 的内接三角形,,, 是直径,,则 的长为
A. B. C. D.
如图,在 的正方形网格中,每个小正方形的边长都是 ,点 ,, 均在网格交点上, 是 的外接圆,则 的值为
A. B. C. D.
如图,在 中,,, 平分 ,交 于点 ,,垂足为 .若 ,则 的长为
A. B. C. D.
如图,平面直角坐标系中,点 在第一象限,点 在 轴的正半轴上,,.将 绕点 逆时针旋转 ,点 的对应点 的坐标是
A. B.
C. D.
为宣传上海世博会,小亮设计了形状如图所示的彩旗,其中 ,,点 在 上,,则 的长为
A. B. C. D.
二、填空题(共5题)
如图,在 中,,,,则 .
等腰直角三角形中,若斜边长为 ,则直角边的长为 .
如图,在 中,,点 是 上一点,,若 ,,则 .
如图,点 是正方形 内一点,且点 到点 ,, 的距离分别为 ,,,则正方形 的面积为 .
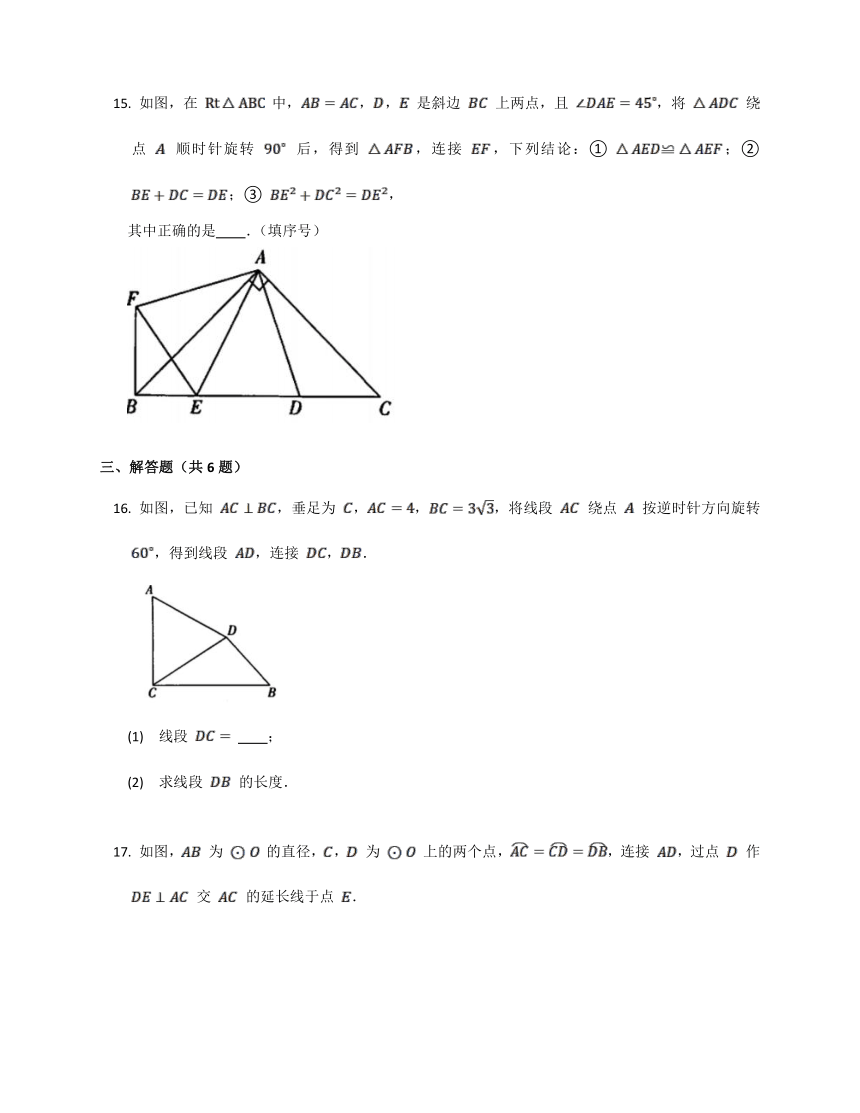
如图,在 中,,, 是斜边 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,下列结论:① ;② ;③ ,
其中正确的是 .(填序号)
三、解答题(共6题)
如图,已知 ,垂足为 ,,,将线段 绕点 按逆时针方向旋转 ,得到线段 ,连接 ,.
(1) 线段 ;
(2) 求线段 的长度.
如图, 为 的直径,, 为 上的两个点,,连接 ,过点 作 交 的延长线于点 .
(1) 求证: 是 的切线;
(2) 若直径 ,求 的长.
如图,在 中,,以 为直径的 交 边于点 ,过点 作 ,与过点 的切线交于点 ,连接 .
(1) 求证:;
(2) 若 ,,求 的长.
如图,在正方形 中,, 是对角线 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,求证:
(1) 是 的平分线;
(2) .
如图, 中,,,,若点 从点 出发以每秒 的速度向点 运动,设运动时间为 秒.
(1) 若点 恰好在 的平分线上,求出此时 的值;
(2) 若点 使得 ,求出此时 的值.
探究问题:
(1) 阅读理解:
①如图(A),在 所在平面上存在一点 ,若它到 三个顶点的距离之和最小,则称点 为 的费马点,此时 的值为 的费马距离.
②如图(B),若四边形 的四个顶点在同一个圆上,则有 ,此为托勒密定理.
知识迁移:
①请你利用托勒密定理解决如下问题:
如图(C),已知点 为等边 外接圆的 上任意一点.求证:;
②根据()①的结论,我们有如下探寻 (其中 ,, 均小于 )的费马点和费马距离的方法:
第一步:如图(D),在 的外部以 为一边作等边 及其外接圆;
第二步:在 上任取一点 ,连接 ,,,.易知 ;
第三步:请你根据()①中定义,在图(D)中找出 的费马点 ,则线段 的长度即为 的费马距离.
(2) 知识应用:今年以来某市持续干旱,许多村庄出现了人、畜饮水困难的问题,为解决老百姓的饮水问题,解放军某部来到该市某地打井取水.已知三村庄 ,, 构成了如图(E)所示的 (其中 ,, 均小于 ),现选取一点 打水井,使从水井 到三村庄 ,, 所铺设的输水管总长度最小,求输水管总长度的最小值.
答案
一、选择题(共10题)
1. 【答案】D
【解析】如图,过点 作 于点 ,
易得 ,,
边上的高 ,
在 中,,
.
【知识点】正弦、勾股定理
2. 【答案】D
【解析】根据勾股定理的逆定理判断:验证两条较短边长的平方和是否等于最长边长的平方.
【知识点】勾股逆定理
3. 【答案】A
【解析】 在 中,,,
,,
.
【知识点】勾股定理、30度所对的直角边等于斜边的一半
4. 【答案】C
【解析】如图,过点 作 于点 ,
由题意可知, 是边长为 的等边三角形,
在 中,
,,
,
即原来的纸条宽为 .
【知识点】等边三角形是轴对称图形、正多边形的有关计算、勾股定理
5. 【答案】B
【解析】 是 的切线,点 为切点,
,
,
,
,
,
,
.
【知识点】勾股定理、切线的性质、圆周角定理及其推理
6. 【答案】B
【解析】连接 ,
,,
,
,
,
是直径,
,
,
,
,
.
【知识点】勾股定理、圆内接四边形的性质、圆周角定理及其推理
7. 【答案】B
【解析】如图,作直径 ,连接 ,
由勾股定理得 ,在 中,,
,
.
【知识点】圆周角定理及其推理、勾股定理、余弦
8. 【答案】A
【解析】如图,过 作 于 .
因为 平分 ,,,
所以 .
在 中,,
所以 ,
在 中,,
所以 ,
所以 ,
所以 ,
所以 .
【知识点】角平分线的性质、勾股定理、30度所对的直角边等于斜边的一半
9. 【答案】A
【解析】如图,过点 作 轴于 .
由旋转的性质可知,,,,
在 中,
,,
,
,,
,
的坐标是 .
【知识点】勾股定理、30度所对的直角边等于斜边的一半、坐标平面内图形的旋转变换
10. 【答案】B
【解析】 ,,
,
,
在 中,,,
,
.
【知识点】等腰三角形的性质、勾股定理、30度所对的直角边等于斜边的一半
二、填空题(共5题)
11. 【答案】
【解析】在 中,,,,
,
.
【知识点】余弦、勾股定理
12. 【答案】
【解析】设等腰直角三角形的直角边长为 ,由勾股定理得 ,则 ,,故答案为 .
【知识点】勾股定理、等腰直角三角形
13. 【答案】
【解析】设 ,则 ,
在 中,,
在 中,,
,
,解得 ,
.
【知识点】勾股定理
14. 【答案】
【解析】如图,将 绕点 顺时针旋转 得到 ,连接 ,过点 作 于 .
,,
,
,,
,
,
,
,
,
,, 三点共线,
,
,
,
,
,
正方形 的面积为 .
【知识点】勾股定理、旋转及其性质、正方形的性质
15. 【答案】①③
【解析】如图,
由已知得,,
又 ,
,
由旋转的性质得,,,
,
又 ,
,故①正确.
,,
,
由旋转的性质知 ,
,
在 中,,
由 ,得 ,
由旋转的性质得 ,
,故③正确,②不正确.
综上,①③正确.
【知识点】勾股定理、旋转及其性质
三、解答题(共6题)
16. 【答案】
(1)
(2) 过点 作 于点 ,
因为 是等边三角形,
所以 ,
又因为 ,
所以 ,
所以在 中,,,
所以 .
所以在 中,.
【解析】
(1) 因为 ,,
所以 是等边三角形,
所以 .
【知识点】旋转及其性质、勾股定理
17. 【答案】
(1) 如图,连接 ,
,
,
,
,
,
,
,
,
,
,
,
,
是 的切线.
(2) 如图,连接 ,
为 的直径,
,
,,
,
.
【知识点】圆周角定理及其推理、弧、弦、圆心角的关系定理、30度所对的直角边等于斜边的一半、勾股定理、切线的判定
18. 【答案】
(1) ,
.
,
,
,
是 的直径,
.
是 的切线,
.
,
,
.
又 ,
,
.
(2) ,,
.
在 中,.
在 中,,
即 的长为 .
【知识点】圆周角定理及其推理、切线的性质、勾股定理
19. 【答案】
(1) 将 绕点 顺吋针旋转 后,得到 ,
,,,
,
,
,
.
在 和 中,
,
,
是 的平分线..
(2) 由()得 ,
,
由旋转知 ,
又 ,
,即 .
在 中,,
则 .
【知识点】旋转及其性质、勾股定理、边角边
20. 【答案】
(1) 作 于 ,如图,,
,,,
,
平分 ,
,
,
,
解得 ,
即此时 的值为 .
(2) ,,
,
在 中,
,
,解得 ,
即此时 的值为 .
【知识点】勾股定理、角平分线的性质
21. 【答案】
(1) ①由托勒密定理可知 .
是等边三角形,
,
.
② ;
点 的位置( 与 的交点)如图所示:
(2) 以 为一边作如图所示的等边 ,连接 ,则线段 的长即为 的费马距离.
为等边三角形,,
,,
,
,
在 中,
,,
,
从水井 到三村庄 ,, 所铺设的输水管总长度的最小值为 .
【知识点】等边三角形的概念、勾股定理、等边三角形三个角相等,都等于60°
(共21题)
一、选择题(共10题)
如图,在 的网格中,点 ,, 都在格点上,每个小正方形的边长为 ,则 的值为
A. B. C. D.
以下列长度的线段为边长作三角形,可以构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
如图所示,小颖利用有一个锐角是 的三角板测量一棵树的高度,已知她与树之间的水平距离 为 , 为 (即小颖的眼睛距地面的距离),那么这棵树高是
A. B. C. D.
如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为 的正六边形,则原来的纸条宽为
A. B. C. D.
如图,点 ,, 在 上,, 是 的切线,点 为切点, 的延长线交 于点 ,若 的长为 ,则 的长是
A. B. C. D.
如图, 是 的内接三角形,,, 是直径,,则 的长为
A. B. C. D.
如图,在 的正方形网格中,每个小正方形的边长都是 ,点 ,, 均在网格交点上, 是 的外接圆,则 的值为
A. B. C. D.
如图,在 中,,, 平分 ,交 于点 ,,垂足为 .若 ,则 的长为
A. B. C. D.
如图,平面直角坐标系中,点 在第一象限,点 在 轴的正半轴上,,.将 绕点 逆时针旋转 ,点 的对应点 的坐标是
A. B.
C. D.
为宣传上海世博会,小亮设计了形状如图所示的彩旗,其中 ,,点 在 上,,则 的长为
A. B. C. D.
二、填空题(共5题)
如图,在 中,,,,则 .
等腰直角三角形中,若斜边长为 ,则直角边的长为 .
如图,在 中,,点 是 上一点,,若 ,,则 .
如图,点 是正方形 内一点,且点 到点 ,, 的距离分别为 ,,,则正方形 的面积为 .
如图,在 中,,, 是斜边 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,下列结论:① ;② ;③ ,
其中正确的是 .(填序号)
三、解答题(共6题)
如图,已知 ,垂足为 ,,,将线段 绕点 按逆时针方向旋转 ,得到线段 ,连接 ,.
(1) 线段 ;
(2) 求线段 的长度.
如图, 为 的直径,, 为 上的两个点,,连接 ,过点 作 交 的延长线于点 .
(1) 求证: 是 的切线;
(2) 若直径 ,求 的长.
如图,在 中,,以 为直径的 交 边于点 ,过点 作 ,与过点 的切线交于点 ,连接 .
(1) 求证:;
(2) 若 ,,求 的长.
如图,在正方形 中,, 是对角线 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,求证:
(1) 是 的平分线;
(2) .
如图, 中,,,,若点 从点 出发以每秒 的速度向点 运动,设运动时间为 秒.
(1) 若点 恰好在 的平分线上,求出此时 的值;
(2) 若点 使得 ,求出此时 的值.
探究问题:
(1) 阅读理解:
①如图(A),在 所在平面上存在一点 ,若它到 三个顶点的距离之和最小,则称点 为 的费马点,此时 的值为 的费马距离.
②如图(B),若四边形 的四个顶点在同一个圆上,则有 ,此为托勒密定理.
知识迁移:
①请你利用托勒密定理解决如下问题:
如图(C),已知点 为等边 外接圆的 上任意一点.求证:;
②根据()①的结论,我们有如下探寻 (其中 ,, 均小于 )的费马点和费马距离的方法:
第一步:如图(D),在 的外部以 为一边作等边 及其外接圆;
第二步:在 上任取一点 ,连接 ,,,.易知 ;
第三步:请你根据()①中定义,在图(D)中找出 的费马点 ,则线段 的长度即为 的费马距离.
(2) 知识应用:今年以来某市持续干旱,许多村庄出现了人、畜饮水困难的问题,为解决老百姓的饮水问题,解放军某部来到该市某地打井取水.已知三村庄 ,, 构成了如图(E)所示的 (其中 ,, 均小于 ),现选取一点 打水井,使从水井 到三村庄 ,, 所铺设的输水管总长度最小,求输水管总长度的最小值.
答案
一、选择题(共10题)
1. 【答案】D
【解析】如图,过点 作 于点 ,
易得 ,,
边上的高 ,
在 中,,
.
【知识点】正弦、勾股定理
2. 【答案】D
【解析】根据勾股定理的逆定理判断:验证两条较短边长的平方和是否等于最长边长的平方.
【知识点】勾股逆定理
3. 【答案】A
【解析】 在 中,,,
,,
.
【知识点】勾股定理、30度所对的直角边等于斜边的一半
4. 【答案】C
【解析】如图,过点 作 于点 ,
由题意可知, 是边长为 的等边三角形,
在 中,
,,
,
即原来的纸条宽为 .
【知识点】等边三角形是轴对称图形、正多边形的有关计算、勾股定理
5. 【答案】B
【解析】 是 的切线,点 为切点,
,
,
,
,
,
,
.
【知识点】勾股定理、切线的性质、圆周角定理及其推理
6. 【答案】B
【解析】连接 ,
,,
,
,
,
是直径,
,
,
,
,
.
【知识点】勾股定理、圆内接四边形的性质、圆周角定理及其推理
7. 【答案】B
【解析】如图,作直径 ,连接 ,
由勾股定理得 ,在 中,,
,
.
【知识点】圆周角定理及其推理、勾股定理、余弦
8. 【答案】A
【解析】如图,过 作 于 .
因为 平分 ,,,
所以 .
在 中,,
所以 ,
在 中,,
所以 ,
所以 ,
所以 ,
所以 .
【知识点】角平分线的性质、勾股定理、30度所对的直角边等于斜边的一半
9. 【答案】A
【解析】如图,过点 作 轴于 .
由旋转的性质可知,,,,
在 中,
,,
,
,,
,
的坐标是 .
【知识点】勾股定理、30度所对的直角边等于斜边的一半、坐标平面内图形的旋转变换
10. 【答案】B
【解析】 ,,
,
,
在 中,,,
,
.
【知识点】等腰三角形的性质、勾股定理、30度所对的直角边等于斜边的一半
二、填空题(共5题)
11. 【答案】
【解析】在 中,,,,
,
.
【知识点】余弦、勾股定理
12. 【答案】
【解析】设等腰直角三角形的直角边长为 ,由勾股定理得 ,则 ,,故答案为 .
【知识点】勾股定理、等腰直角三角形
13. 【答案】
【解析】设 ,则 ,
在 中,,
在 中,,
,
,解得 ,
.
【知识点】勾股定理
14. 【答案】
【解析】如图,将 绕点 顺时针旋转 得到 ,连接 ,过点 作 于 .
,,
,
,,
,
,
,
,
,
,, 三点共线,
,
,
,
,
,
正方形 的面积为 .
【知识点】勾股定理、旋转及其性质、正方形的性质
15. 【答案】①③
【解析】如图,
由已知得,,
又 ,
,
由旋转的性质得,,,
,
又 ,
,故①正确.
,,
,
由旋转的性质知 ,
,
在 中,,
由 ,得 ,
由旋转的性质得 ,
,故③正确,②不正确.
综上,①③正确.
【知识点】勾股定理、旋转及其性质
三、解答题(共6题)
16. 【答案】
(1)
(2) 过点 作 于点 ,
因为 是等边三角形,
所以 ,
又因为 ,
所以 ,
所以在 中,,,
所以 .
所以在 中,.
【解析】
(1) 因为 ,,
所以 是等边三角形,
所以 .
【知识点】旋转及其性质、勾股定理
17. 【答案】
(1) 如图,连接 ,
,
,
,
,
,
,
,
,
,
,
,
,
是 的切线.
(2) 如图,连接 ,
为 的直径,
,
,,
,
.
【知识点】圆周角定理及其推理、弧、弦、圆心角的关系定理、30度所对的直角边等于斜边的一半、勾股定理、切线的判定
18. 【答案】
(1) ,
.
,
,
,
是 的直径,
.
是 的切线,
.
,
,
.
又 ,
,
.
(2) ,,
.
在 中,.
在 中,,
即 的长为 .
【知识点】圆周角定理及其推理、切线的性质、勾股定理
19. 【答案】
(1) 将 绕点 顺吋针旋转 后,得到 ,
,,,
,
,
,
.
在 和 中,
,
,
是 的平分线..
(2) 由()得 ,
,
由旋转知 ,
又 ,
,即 .
在 中,,
则 .
【知识点】旋转及其性质、勾股定理、边角边
20. 【答案】
(1) 作 于 ,如图,,
,,,
,
平分 ,
,
,
,
解得 ,
即此时 的值为 .
(2) ,,
,
在 中,
,
,解得 ,
即此时 的值为 .
【知识点】勾股定理、角平分线的性质
21. 【答案】
(1) ①由托勒密定理可知 .
是等边三角形,
,
.
② ;
点 的位置( 与 的交点)如图所示:
(2) 以 为一边作如图所示的等边 ,连接 ,则线段 的长即为 的费马距离.
为等边三角形,,
,,
,
,
在 中,
,,
,
从水井 到三村庄 ,, 所铺设的输水管总长度的最小值为 .
【知识点】等边三角形的概念、勾股定理、等边三角形三个角相等,都等于60°
