角的比较[上学期]

课件25张PPT。知识目标 :1.会比较角的大小;
2.能估计一个角的大小;
3.认识角的平分线;
4.会进行度、分、秒的换算.
能力目标 :培养观察、想象、估测的能力.
情感与价值观目标：让学生经历主动探索、合作交流的过程,感受数学的魅力.借助三角板估测角的度数.学习目标学习重点角的比较、角平分线、角的度分秒的换算.学习难点第四节 角的比较 郑州市第三十九中学
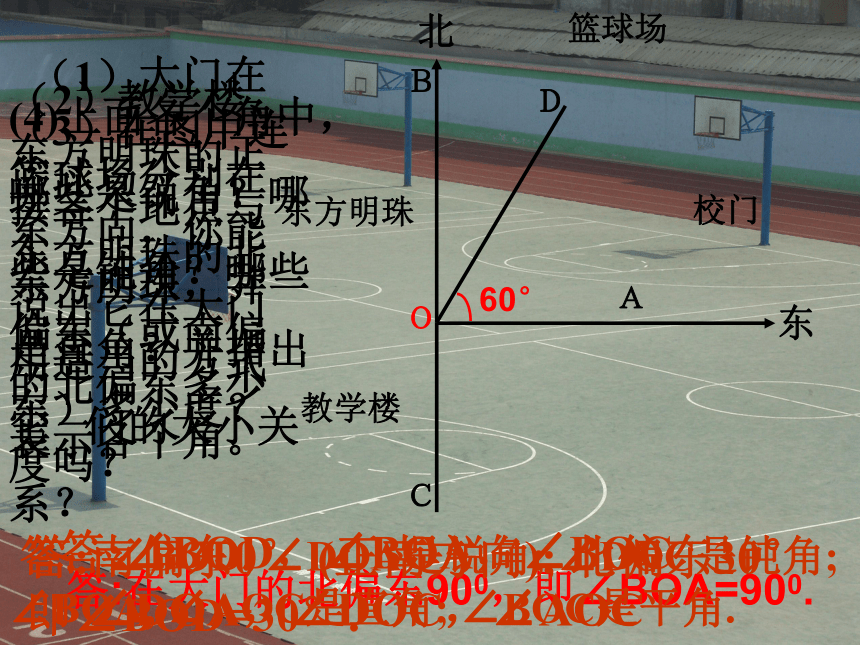
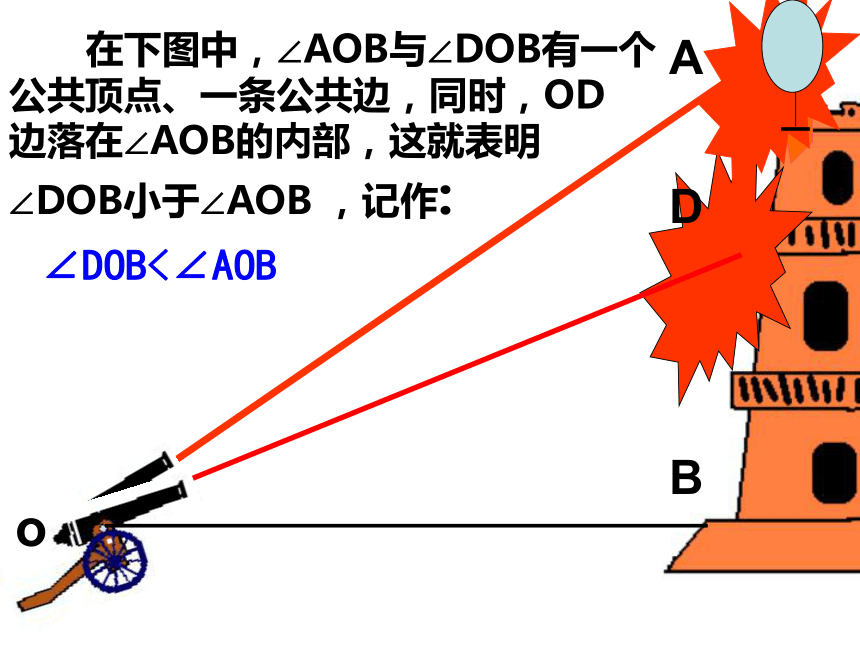
孙洁二七广场３９中35°东方明珠篮球场校门教学楼ＯＡＢＣＤ （1）大门在东方明珠的正东方向，你能说出它在大门的北偏东多少度吗？答:在大门的北偏东900，即∠BOA=900.（2）教学楼、篮球场分别在东方明珠的北偏东（或南偏东）多少度？答:南偏东0° (正南方向); 北偏东30°即∠BOD=30°.60°（3）在图中连接各个地点与东方明珠，并用适当的方式表示各个角。答:∠BOD，∠BOA，∠BOC ∠DOA，∠DOC，∠AOC(4)上面各个角中，哪些是锐角？哪些是钝角？哪些是直角？并指出它 们的大小关系？ 答：∠BOD, ∠DOA是锐角; ∠DOC是钝角; ∠BOA, ∠AOC是直角; ∠BOC是平角.比一比角的大小oABD　　在下图中，∠AOB与∠DOB有一个
公共顶点、一条公共边，同时，OD
边落在∠AOB的内部，这就表明
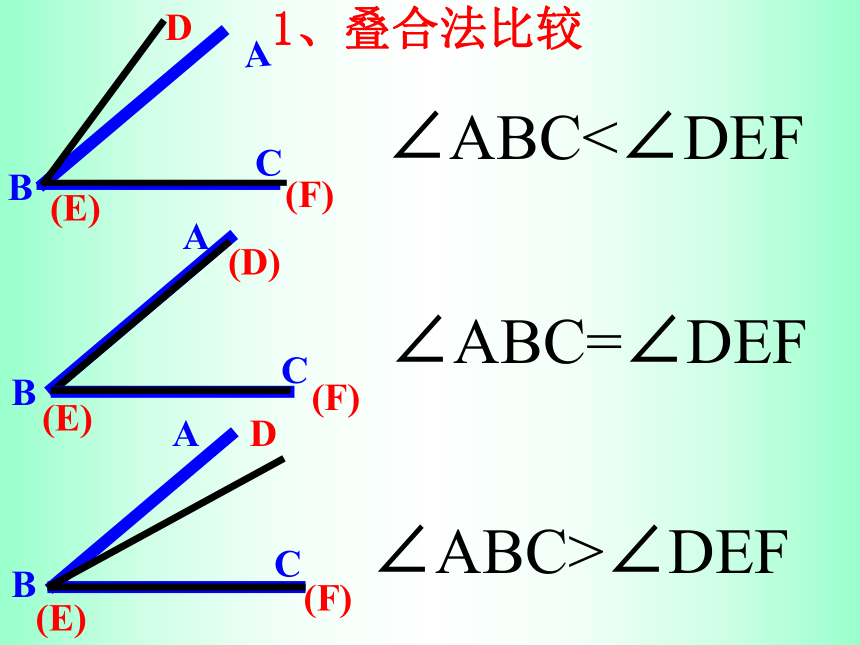
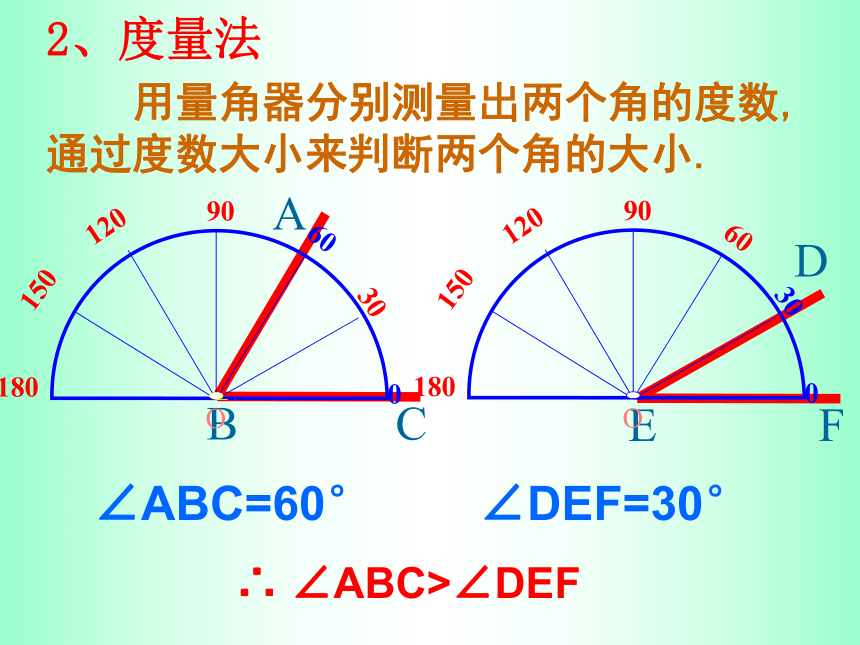
∠DOB小于∠AOB ，记作:∠DOB<∠AOB∠ABC=∠DEF∠ABC<∠DEF∠ABC>∠DEF1、叠合法比较2、度量法∠ABC=60°∠DEF=30°∴ ∠ABC>∠DEF 用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.例1： 根据下图，求解下列问题：
(1)比较∠AOB，∠AOC，∠AOD，∠AOE的大小，并指出其中的锐角、直角、钝角、平角.
　　　解:（1）由图可以看出
∠AOB＜∠AOC＜∠AOD＜∠AOE　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　其中　∠AOB 为锐角，
　　　∠AOC为直角，
　　　∠AOD为钝角，
　　　∠AOE为平角．
例1： 根据下图，求解下列问题：
(2)写出∠AOB, ∠AOC, ∠BOC,
∠AOE中某些角之间的两个等量关系.解：　
(２)∠AOB+ ∠BOC= ∠AOC
2 ∠AOC=∠AOE例1： 根据下图，求解下列问题：
(3)借助三角尺估测∠AOB，∠BOD, ∠COD, ∠AOD的度数. EDCBAOO解:
(3) ∠AOB大约是300
∠BOD大约是750 30o45o30o例1： 根据下图，求解下列问题：
(3)借助三角尺估测∠AOB， ∠BOD, ∠COD, ∠AOD的度数. EDCBAOO解:
(3) ∠COD大约是150 30o45o60o∠AOD大约是1050折一折动动手，做一做 在一张纸上画出一个角并剪下，将这个角对折，使其两边重合，折痕与角两边所成的两个角的大小有什么关系？角的平分线1、定义：一条射线把一个角分成两个相等
的角， 这条射线叫做这个角的平分线． 2、几何语言表达：∵ OC是∠AOB的平分线OABC12∴∠1＝∠2＝ ∠AOB
或∠AOB＝２∠１＝２∠２1习题：
如上图ＯＢ是∠AOC的平分线，OＤ是
∠COE的平分线
（1）若∠AOC=500，则∠BOC=______
（2）若∠AOC=500， ∠ COE=800，
则∠COD=______,∠BOD=______.250650400250400算一算度、分、秒的换算 例:计算
1.45°等于多少分?等于多少秒?
1800″等于多少分?等于多少度?例:计算
1.45°等于多少分?等于多少秒?
1800″等于多少分?等于多少度?解: (1) 60′x1.45=87′, 60 ″ x87=5220 ″,
即1.45o=87′=5220 ″.*课堂小结这节课，你收获了什么？通过这节课，你认为数学和生活的关系是
什么？1、角的比较*叠合法*度量法
2、角的平分线
3、角的度、分、秒的换算 数学来源于生活，又应用于生活，数学和生活密不可分，生活中处处有
数学！作业
P150 随堂练习 （1）
P151 习题 （1）（2） 把两个三角尺按如图所示那样拼在一起，
请确定图中∠B＝＿＿， ∠E＝＿＿，
∠BAD＝＿＿，∠DCE＝＿＿．BCADE60o90o135o45o45o90o60o30o