2022—2023学年人教版数学八年级上册12.3角平分线的性质 课件(共14张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册12.3角平分线的性质 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 755.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 10:12:28 | ||
图片预览


文档简介
(共14张PPT)
12.3 角平分线的性质
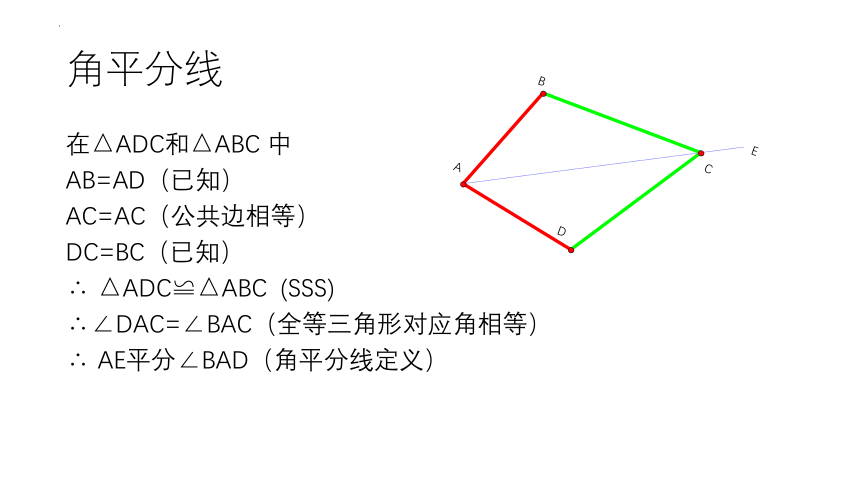
角平分线
在△ADC和△ABC 中
AB=AD(已知)
AC=AC(公共边相等)
DC=BC(已知)
∴ △ADC≌△ABC (SSS)
∴∠DAC=∠BAC(全等三角形对应角相等)
∴ AE平分∠BAD(角平分线定义)
B
D
A
C
E
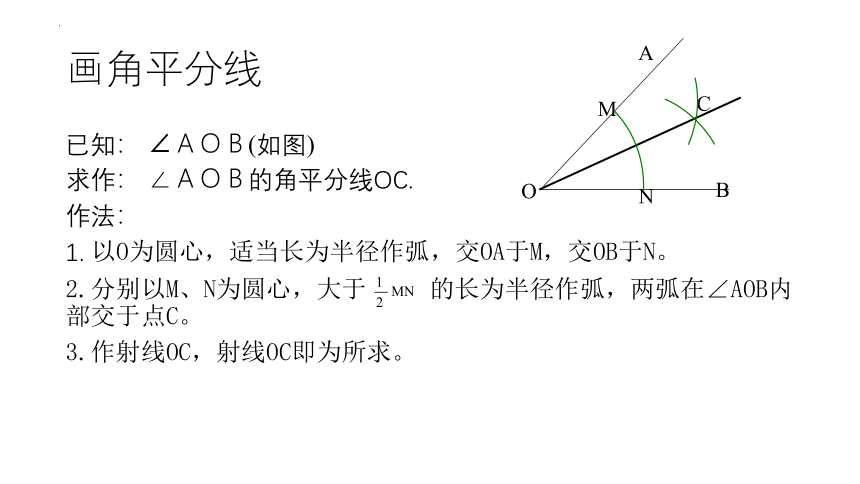
画角平分线
已知: ∠AOB(如图)
求作: ∠AOB的角平分线OC.
作法:
1. 以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
2.分别以M、N为圆心,大于 的长为半径作弧,两弧在∠AOB内部交于点C。
3.作射线OC,射线OC即为所求。
O
A
B
N
M
C
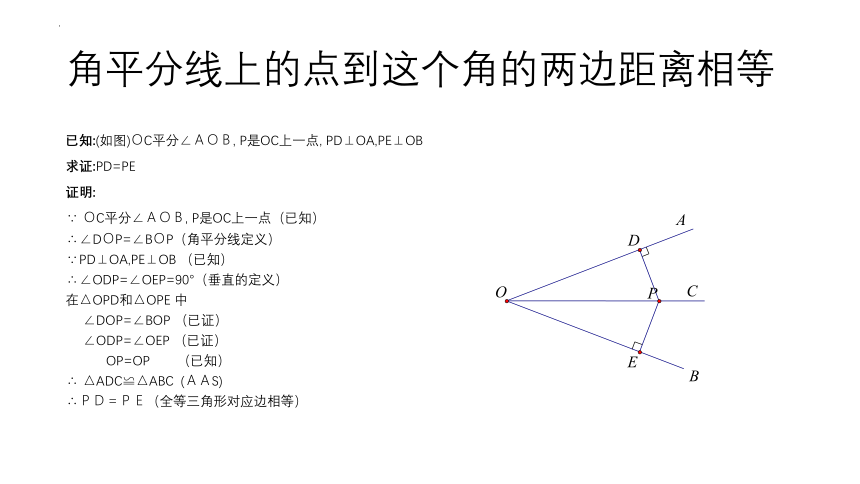
角平分线上的点到这个角的两边距离相等
已知:(如图)OC平分∠AOB, P是OC上一点, PD⊥OA,PE⊥OB
求证:PD=PE
证明:
∵ OC平分∠AOB, P是OC上一点(已知)
∴∠DOP=∠BOP(角平分线定义)
∵PD⊥OA,PE⊥OB (已知)
∴∠ODP=∠OEP=90°(垂直的定义)
在△OPD和△OPE 中
∠DOP=∠BOP (已证)
∠ODP=∠OEP (已证)
OP=OP (已知)
∴ △ADC≌△ABC (AAS)
∴PD=PE(全等三角形对应边相等)
E
D
O
A
B
P
C
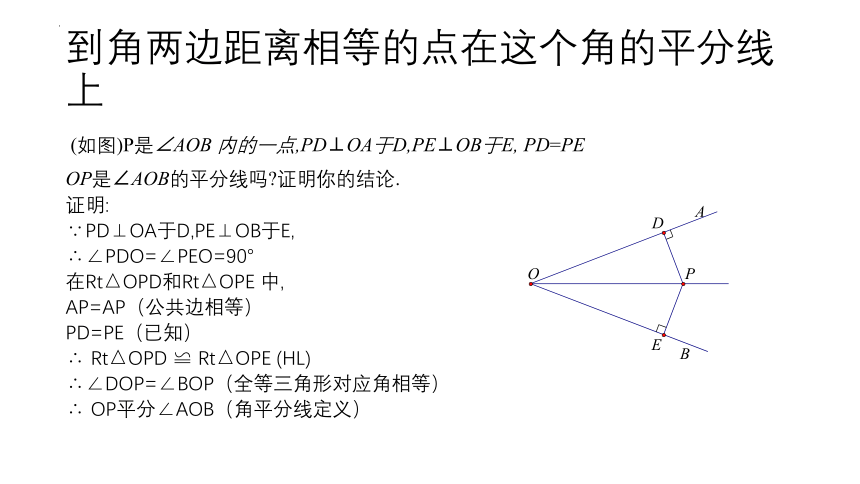
到角两边距离相等的点在这个角的平分线上
(如图)P是∠AOB 内的一点,PD⊥OA于D,PE⊥OB于E, PD=PE
OP是∠AOB的平分线吗 证明你的结论.
证明:
∵PD⊥OA于D,PE⊥OB于E,
∴∠PDO=∠PEO=90°
在Rt△OPD和Rt△OPE 中,
AP=AP(公共边相等)
PD=PE(已知)
∴ Rt△OPD ≌ Rt△OPE (HL)
∴∠DOP=∠BOP(全等三角形对应角相等)
∴ OP平分∠AOB(角平分线定义)
A
B
E
D
O
P
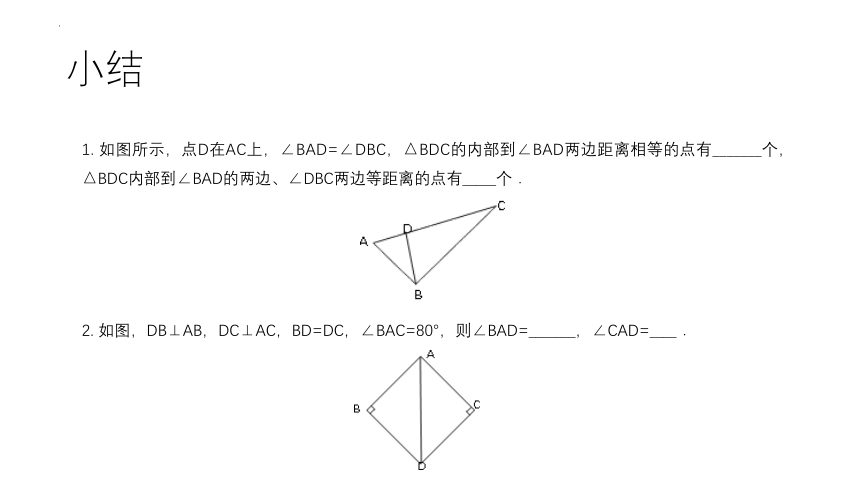
小结
1. 如图所示,点D在AC上,∠BAD=∠DBC,△BDC的内部到∠BAD两边距离相等的点有_______个,△BDC内部到∠BAD的两边、∠DBC两边等距离的点有_____个.
2. 如图,DB⊥AB,DC⊥AC,BD=DC,∠BAC=80°,则∠BAD=_______,∠CAD=____.
3. 与相交的两直线距离相等的点是在 ( )
A.一条射线上 B.一条直线上
C.两条互相垂直的直线上 D.以上都不对
4. 下列结论中,错误的是 ( )
A.到已知角两边距离相等的点都在同一条直线上
B.一条直线上有一点到已知角的两边距离相等,这条直线平分已知角
C.到角的两边距离相等的点,与角顶点的连线平分这个角
D.角内有两点各自到角的两边的距离相等,经过这两点的直线平分这个角
5. 如图11.3-12,已知BD平分∠ABC,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M、N为垂足.求证:PM=PN
6. 如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是 。
7. 已知△ABC中,∠A=80°,∠B和∠C的角平分线交于O点,则∠BOC= 。
8. 在△ABC中,∠B=∠ACB,CD是∠ACB的角平分线,已知∠ADC=105°,则∠A的度数为( )
A.40° B.36° C.70° D.60°
9. 如图,BD=CD,BF⊥AC于F,CE⊥AB于E。求证:点D在∠BAC的角平分线上。
10. 到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
11. 如图,点D、B分别在∠A的两边上,C是∠A内一点,AB = AD,BC = CD,CE⊥AD于E,CF⊥AF于F.
求证:CE = CF
12. 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E。
(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD
B
A
C
D
E
13. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
A
B
C
E
F
D
14. 已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.
A
A
A
A
A
A
A
D
N
E
B
F
M
C
A
12.3 角平分线的性质
角平分线
在△ADC和△ABC 中
AB=AD(已知)
AC=AC(公共边相等)
DC=BC(已知)
∴ △ADC≌△ABC (SSS)
∴∠DAC=∠BAC(全等三角形对应角相等)
∴ AE平分∠BAD(角平分线定义)
B
D
A
C
E
画角平分线
已知: ∠AOB(如图)
求作: ∠AOB的角平分线OC.
作法:
1. 以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
2.分别以M、N为圆心,大于 的长为半径作弧,两弧在∠AOB内部交于点C。
3.作射线OC,射线OC即为所求。
O
A
B
N
M
C
角平分线上的点到这个角的两边距离相等
已知:(如图)OC平分∠AOB, P是OC上一点, PD⊥OA,PE⊥OB
求证:PD=PE
证明:
∵ OC平分∠AOB, P是OC上一点(已知)
∴∠DOP=∠BOP(角平分线定义)
∵PD⊥OA,PE⊥OB (已知)
∴∠ODP=∠OEP=90°(垂直的定义)
在△OPD和△OPE 中
∠DOP=∠BOP (已证)
∠ODP=∠OEP (已证)
OP=OP (已知)
∴ △ADC≌△ABC (AAS)
∴PD=PE(全等三角形对应边相等)
E
D
O
A
B
P
C
到角两边距离相等的点在这个角的平分线上
(如图)P是∠AOB 内的一点,PD⊥OA于D,PE⊥OB于E, PD=PE
OP是∠AOB的平分线吗 证明你的结论.
证明:
∵PD⊥OA于D,PE⊥OB于E,
∴∠PDO=∠PEO=90°
在Rt△OPD和Rt△OPE 中,
AP=AP(公共边相等)
PD=PE(已知)
∴ Rt△OPD ≌ Rt△OPE (HL)
∴∠DOP=∠BOP(全等三角形对应角相等)
∴ OP平分∠AOB(角平分线定义)
A
B
E
D
O
P
小结
1. 如图所示,点D在AC上,∠BAD=∠DBC,△BDC的内部到∠BAD两边距离相等的点有_______个,△BDC内部到∠BAD的两边、∠DBC两边等距离的点有_____个.
2. 如图,DB⊥AB,DC⊥AC,BD=DC,∠BAC=80°,则∠BAD=_______,∠CAD=____.
3. 与相交的两直线距离相等的点是在 ( )
A.一条射线上 B.一条直线上
C.两条互相垂直的直线上 D.以上都不对
4. 下列结论中,错误的是 ( )
A.到已知角两边距离相等的点都在同一条直线上
B.一条直线上有一点到已知角的两边距离相等,这条直线平分已知角
C.到角的两边距离相等的点,与角顶点的连线平分这个角
D.角内有两点各自到角的两边的距离相等,经过这两点的直线平分这个角
5. 如图11.3-12,已知BD平分∠ABC,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M、N为垂足.求证:PM=PN
6. 如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是 。
7. 已知△ABC中,∠A=80°,∠B和∠C的角平分线交于O点,则∠BOC= 。
8. 在△ABC中,∠B=∠ACB,CD是∠ACB的角平分线,已知∠ADC=105°,则∠A的度数为( )
A.40° B.36° C.70° D.60°
9. 如图,BD=CD,BF⊥AC于F,CE⊥AB于E。求证:点D在∠BAC的角平分线上。
10. 到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
11. 如图,点D、B分别在∠A的两边上,C是∠A内一点,AB = AD,BC = CD,CE⊥AD于E,CF⊥AF于F.
求证:CE = CF
12. 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E。
(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD
B
A
C
D
E
13. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
A
B
C
E
F
D
14. 已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.
A
A
A
A
A
A
A
D
N
E
B
F
M
C
A
