2022—2023学年人教版数学七年级上册2.2整式的加减 课件(共30张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册2.2整式的加减 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 135.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 10:18:24 | ||
图片预览





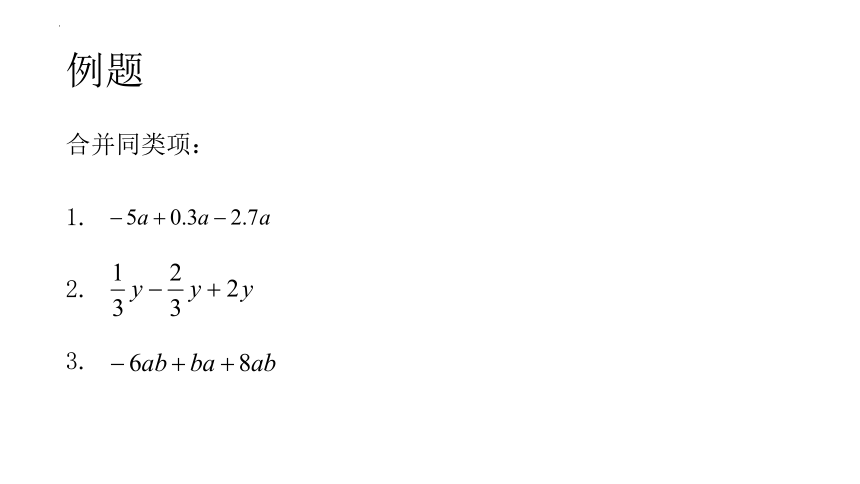



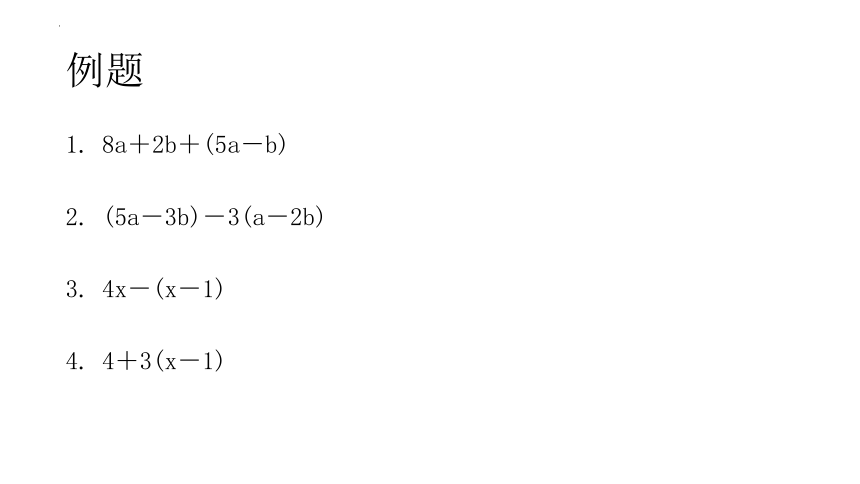


文档简介
(共30张PPT)
2.2 整式的加减
同类项
1. 同类项的概念:所含字母相同,并且相同字母的指数也相同的项叫做同类项.
2. 同类项的识别:找相同——“所含字母相同,相同字母的指数相同”;避无关——“与系数、字母排列顺序无关”;常数都是同类项. 可简化为“同类项,除了系数都一样,常数都是同类项.”
例题
判断下列说法是否正确,正确的在括号内打“√”,错误的打“×”
(1) 与 是同类项( )
(2) 与 是同类项( )
(3) 与 是同类项( )
(4) 与 是同类项( )
(5) 与 是同类项( )
合并同类项
1. 把多项式中的同类项合并成一项可以化简多项式.
2. 合并同类项法则:把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
3. 合并同类项的具体做法:
(1)准确地找同类项;
(2)逆用分配律,把同类项的系数加在一起(用小括号),字母和字母的指数不变;
(3)写出合并后的结果.
注意:
(1)如果两个同类项的系数互为相反数,合并同类项后,结果为0.
(2)合并同类项时,只能把同类项合并成一项,不是同类项的不能合并. 不能合并的项,在每步运算中不要漏掉.
(3)在多项式中,只要不再有同类项,就是最后的结果,结果可能是单项式,也可能是多项式.
例题
合并同类项:
1.
2.
3.
练习
合并下列各式的同类项:
1. 15x+4x-10x;
2. -p2-p2-p2;
3. 6x-10x2+12x2-5x;
4. x2y-3xy2+2yx2-y2x.
去括号与添括号法则
1. 去括号法则:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里的各项都不变符号;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里的各项都改变符号.
如:+(a+b-c)=a+b-c,-(a+b-c)=-a-b+c.
2. 添括号法则:所添括号前面是“+”号,括到括号里的各项都不变符号;所添括号前面是“-”号,括到括号里的各项都改变符号.
如:a-b-c=+(a-b-c),a-b-c=-(-a+b+c).
顺口溜:
去括号,看符号:
是“+”号,不变号;
是“-”号,全变号。
例题
8a+2b+(5a-b)
(5a-3b)-3(a-2b)
4x-(x-1)
4+3(x-1)
练习
判断下列各题中的正误:
1、4a+(-a+3)=4a+a+3=5a+3
2、 (2a-b)-(6b-7a)=2a-b-6b-7a=-5a-7b
3、3(x-2y)-2(4x-6y)=3x-6y-8x+6y=-5x
4、-(2x+4y)+(6x-2y+1)=-2x-4y+6x-2y=4x-6y
5、4-3(2x-5)=4-6x+15=19-6x
整式的加减法法则
一般地,几个整式相加减,如果有括号就先去括号,然后合并同类项.
(1)整式的加减运算,实质是正确地去括号、合并同类项,以及进行实际背景的加减运算.
(2)几个多项式相加,可以省略括号,直接写成相加的形式
(3)两个多项式相减,被减数可不加括号,但减数一定要添加括号. (4)在进行整式加减运算时,可把着眼点放在问题的整体上,用整体思想考虑问题,可使计算简化.
例题
计算:
(1)3x2- [7x-(4x-3)-2x2];
(2)(2xy-y)-(-y+yx);
(3)5(a2b-3ab2)-2(a2b-7ab2).
整式的化简求值
应用整式的加减的运算法则进行化简求值时,一般先去括号、合并同类项,再代入字母的值进行计算,简记为:“一化,二代,三计算”.
例题
先化简,再求值:(4a2-3a)-(1-4a+4a2),其中a=-2.
练习
先化简,再求值:
1. 3x2-8x+x3-12x2-3x3+1,其中x=2;
2. 4x2+2xy+9y2-2x2-3xy+y2,其中x=2,y=1.
小结
1. 同类项:所含字母 ,并且相同字母的指数也
的项叫做同类项. 几个常数项也是 .
2. 合并同类项:把多项式中的同类项合并成一项,叫做合并同类项. 合并同类项后,所得项的系数是合并前各同类项的系数的 ,且字母部分不变.
3. 去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号 ;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号 .
4. 整式加减的运算法则:一般地,几个整式相加减,如果有括号就先 ,然后再 .
5. 化简:-5a+(3a-2)-(3a-7)
6.已知在数轴上位置如图所示,化简: b-a + a-b
0
a
b
7. 下列去括号正确的是( )
A.2a-(3b-c)=2a-3b-c
B.3a+(2b-3c)-(-a)=3a+2b-3c-a
C.6a-(-2b+5)=6a+2b+5
D.-(5x-3y)-(2x-y)=-5x+3y-2x+y
8. 下列多项式加减结果正确的是( )
A.(x2+x-1)-(x4-x2+x)=x4+2x-1
B.-(4a2b-3ab2)+(-3a2b+6ab2)=-a2b-3ab2
C.(5x4+5)+(-5x4+4)=x4+9
D.(3x2-5)-2(x2-1)=x2-3
D
D
9.化简:a-[4a-2(a-2b)]=___________.
10.若a-b=3,ab=-3,则3a-3b-6ab=_______.
11.若当x=1时,整式ax3+bx+7的值为4,则当x=-1时,整式ax3+bx+7的值为_______.
-a-4b
27
10
12.计算:
(1)2x2-3x+4x2-6x-5;
解:原式=6x2-9x-5
(2)3xy+4x2y-3xy2-5x2y;
解:原式=3xy-x2y-3xy2
(3)5(a-b)2-7(a-b)+3(a-b)2-9(a-b);
解:原式=8(a-b)2-16(a-b)
(4)3(a2-2ab)-2(-3ab+b2).
解:原式=3a2-6ab+6ab-2b2=3a2-2b2
13.化简求值:
(1)5a3-2a2+a-2(a3-3a2)-1,a=-1;
解:原式=3a3+4a2+a-1,当a=-1时,原式=-1
(2)4a2b-[3ab2-2(3a2b-1)],其中a=-0.1,b=1;
解:原式=10a2b-3ab2-2,当a=-0.1,b=1时,原式=-1.6
(3)3x-{4x-2[-(5x-1)+3]},其中x=-2;
解:原式=3x-4x+2(-5x+1+3)=-11x+8,当x=-2时,原式=-11×(-2)+8=30
14.如果单项式xa+1y3与2x3yb是同类项,那么ab=_______.
15.若3xm+5y2与x3yn的和是单项式,则mn=______.
16.若-4xay+x2yb=-3x2y,则a+b=______.
17.把(a-b)看成一个字母,合并同类项8(a-b)2-7(a-b)+(a-b)2-5(a-b)的结果为__________________.
18.若多项式a2+2kab与d2-6ab的和不含ab项,则k=_______.
19. 合并同类项:
(1)3x2-1-2x-5+3x-x2;
(2)-0.8a2b-6ab-1.2a2b+5ab+a2b;
(3)4ax+3by-6ax+4bx-3by.
B
C
20. 下列各式去括号后正确的是( )
A.a-(b-c)=a+b-c
B.a-(b-c)=a-b+c
C.a-(b-c)=a-b-c
D.a+(b-c)=a+b+c
21. 下列各式中,去括号后得x-y+z的是( )
A.x-(y+z) B.-(x-y)+z
C.x-(y-z) D.-(x+y)+z
a+b-c
a+b-c
22. 去掉下列各式中的括号:
(1)a-(-b+c)=____________;
(2)a+(b-c)=_______________;
(3)(a-2b)-(b2-2a2)=___________________.
23. 化简:
(1)(4ab-b2)-2(a2+2ab-b2);
(2)-3(2x2-xy)+4(x2+xy-6).
a-2b-b2+2a2
解:原式=-2a2+b2
解:原式=-2x2+7xy-24
解:原式=-2x3-9x2-8x+1=-67
24. 先化简,再求值:
(1)3x2-8x+x3-12x2-3x3+1,其中x=2;
(2)4x2+2xy+9y2-2x2-3xy+y2,其中x=2,y=1.
解:原式=2x2-xy+10y2=16
C
A
25. 计算a+b+(a-b)的最后结果是( )
A.2a+2b B.2b
C.2a D.0
26. 计算5(2x-3)+4(3-2x)的结果为( )
A.2x-3 B.2x+9
C.8x-3 D.18x-3
27. 当x=5时,(x2-x)-(x2-2x+1)=( )
A.-14 B.4
C.-4 D.1
B
B
28. 若A=x2-2xy+y2,B=x2+2xy+y2,则4xy=( )
A.A+B B.B-A
C.A-B D.2A-2B
29. 减去-4a等于3a2-2a-1的多项式是( )
A.3a2-6a-1 B.5a2-1
C.3a2+2a-1 D.3a2+6a-1
30. 化简:(x2+y2)-3(x2-2y2)=_______________.
31. 多项式x2-x+5减去3x2-4的结果是________________.
32. 多项式______________与m2+m-2的和是m2-2m.
A
-2x2+7y2
-2x2-x+9
-3m+2
2.2 整式的加减
同类项
1. 同类项的概念:所含字母相同,并且相同字母的指数也相同的项叫做同类项.
2. 同类项的识别:找相同——“所含字母相同,相同字母的指数相同”;避无关——“与系数、字母排列顺序无关”;常数都是同类项. 可简化为“同类项,除了系数都一样,常数都是同类项.”
例题
判断下列说法是否正确,正确的在括号内打“√”,错误的打“×”
(1) 与 是同类项( )
(2) 与 是同类项( )
(3) 与 是同类项( )
(4) 与 是同类项( )
(5) 与 是同类项( )
合并同类项
1. 把多项式中的同类项合并成一项可以化简多项式.
2. 合并同类项法则:把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
3. 合并同类项的具体做法:
(1)准确地找同类项;
(2)逆用分配律,把同类项的系数加在一起(用小括号),字母和字母的指数不变;
(3)写出合并后的结果.
注意:
(1)如果两个同类项的系数互为相反数,合并同类项后,结果为0.
(2)合并同类项时,只能把同类项合并成一项,不是同类项的不能合并. 不能合并的项,在每步运算中不要漏掉.
(3)在多项式中,只要不再有同类项,就是最后的结果,结果可能是单项式,也可能是多项式.
例题
合并同类项:
1.
2.
3.
练习
合并下列各式的同类项:
1. 15x+4x-10x;
2. -p2-p2-p2;
3. 6x-10x2+12x2-5x;
4. x2y-3xy2+2yx2-y2x.
去括号与添括号法则
1. 去括号法则:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里的各项都不变符号;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里的各项都改变符号.
如:+(a+b-c)=a+b-c,-(a+b-c)=-a-b+c.
2. 添括号法则:所添括号前面是“+”号,括到括号里的各项都不变符号;所添括号前面是“-”号,括到括号里的各项都改变符号.
如:a-b-c=+(a-b-c),a-b-c=-(-a+b+c).
顺口溜:
去括号,看符号:
是“+”号,不变号;
是“-”号,全变号。
例题
8a+2b+(5a-b)
(5a-3b)-3(a-2b)
4x-(x-1)
4+3(x-1)
练习
判断下列各题中的正误:
1、4a+(-a+3)=4a+a+3=5a+3
2、 (2a-b)-(6b-7a)=2a-b-6b-7a=-5a-7b
3、3(x-2y)-2(4x-6y)=3x-6y-8x+6y=-5x
4、-(2x+4y)+(6x-2y+1)=-2x-4y+6x-2y=4x-6y
5、4-3(2x-5)=4-6x+15=19-6x
整式的加减法法则
一般地,几个整式相加减,如果有括号就先去括号,然后合并同类项.
(1)整式的加减运算,实质是正确地去括号、合并同类项,以及进行实际背景的加减运算.
(2)几个多项式相加,可以省略括号,直接写成相加的形式
(3)两个多项式相减,被减数可不加括号,但减数一定要添加括号. (4)在进行整式加减运算时,可把着眼点放在问题的整体上,用整体思想考虑问题,可使计算简化.
例题
计算:
(1)3x2- [7x-(4x-3)-2x2];
(2)(2xy-y)-(-y+yx);
(3)5(a2b-3ab2)-2(a2b-7ab2).
整式的化简求值
应用整式的加减的运算法则进行化简求值时,一般先去括号、合并同类项,再代入字母的值进行计算,简记为:“一化,二代,三计算”.
例题
先化简,再求值:(4a2-3a)-(1-4a+4a2),其中a=-2.
练习
先化简,再求值:
1. 3x2-8x+x3-12x2-3x3+1,其中x=2;
2. 4x2+2xy+9y2-2x2-3xy+y2,其中x=2,y=1.
小结
1. 同类项:所含字母 ,并且相同字母的指数也
的项叫做同类项. 几个常数项也是 .
2. 合并同类项:把多项式中的同类项合并成一项,叫做合并同类项. 合并同类项后,所得项的系数是合并前各同类项的系数的 ,且字母部分不变.
3. 去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号 ;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号 .
4. 整式加减的运算法则:一般地,几个整式相加减,如果有括号就先 ,然后再 .
5. 化简:-5a+(3a-2)-(3a-7)
6.已知在数轴上位置如图所示,化简: b-a + a-b
0
a
b
7. 下列去括号正确的是( )
A.2a-(3b-c)=2a-3b-c
B.3a+(2b-3c)-(-a)=3a+2b-3c-a
C.6a-(-2b+5)=6a+2b+5
D.-(5x-3y)-(2x-y)=-5x+3y-2x+y
8. 下列多项式加减结果正确的是( )
A.(x2+x-1)-(x4-x2+x)=x4+2x-1
B.-(4a2b-3ab2)+(-3a2b+6ab2)=-a2b-3ab2
C.(5x4+5)+(-5x4+4)=x4+9
D.(3x2-5)-2(x2-1)=x2-3
D
D
9.化简:a-[4a-2(a-2b)]=___________.
10.若a-b=3,ab=-3,则3a-3b-6ab=_______.
11.若当x=1时,整式ax3+bx+7的值为4,则当x=-1时,整式ax3+bx+7的值为_______.
-a-4b
27
10
12.计算:
(1)2x2-3x+4x2-6x-5;
解:原式=6x2-9x-5
(2)3xy+4x2y-3xy2-5x2y;
解:原式=3xy-x2y-3xy2
(3)5(a-b)2-7(a-b)+3(a-b)2-9(a-b);
解:原式=8(a-b)2-16(a-b)
(4)3(a2-2ab)-2(-3ab+b2).
解:原式=3a2-6ab+6ab-2b2=3a2-2b2
13.化简求值:
(1)5a3-2a2+a-2(a3-3a2)-1,a=-1;
解:原式=3a3+4a2+a-1,当a=-1时,原式=-1
(2)4a2b-[3ab2-2(3a2b-1)],其中a=-0.1,b=1;
解:原式=10a2b-3ab2-2,当a=-0.1,b=1时,原式=-1.6
(3)3x-{4x-2[-(5x-1)+3]},其中x=-2;
解:原式=3x-4x+2(-5x+1+3)=-11x+8,当x=-2时,原式=-11×(-2)+8=30
14.如果单项式xa+1y3与2x3yb是同类项,那么ab=_______.
15.若3xm+5y2与x3yn的和是单项式,则mn=______.
16.若-4xay+x2yb=-3x2y,则a+b=______.
17.把(a-b)看成一个字母,合并同类项8(a-b)2-7(a-b)+(a-b)2-5(a-b)的结果为__________________.
18.若多项式a2+2kab与d2-6ab的和不含ab项,则k=_______.
19. 合并同类项:
(1)3x2-1-2x-5+3x-x2;
(2)-0.8a2b-6ab-1.2a2b+5ab+a2b;
(3)4ax+3by-6ax+4bx-3by.
B
C
20. 下列各式去括号后正确的是( )
A.a-(b-c)=a+b-c
B.a-(b-c)=a-b+c
C.a-(b-c)=a-b-c
D.a+(b-c)=a+b+c
21. 下列各式中,去括号后得x-y+z的是( )
A.x-(y+z) B.-(x-y)+z
C.x-(y-z) D.-(x+y)+z
a+b-c
a+b-c
22. 去掉下列各式中的括号:
(1)a-(-b+c)=____________;
(2)a+(b-c)=_______________;
(3)(a-2b)-(b2-2a2)=___________________.
23. 化简:
(1)(4ab-b2)-2(a2+2ab-b2);
(2)-3(2x2-xy)+4(x2+xy-6).
a-2b-b2+2a2
解:原式=-2a2+b2
解:原式=-2x2+7xy-24
解:原式=-2x3-9x2-8x+1=-67
24. 先化简,再求值:
(1)3x2-8x+x3-12x2-3x3+1,其中x=2;
(2)4x2+2xy+9y2-2x2-3xy+y2,其中x=2,y=1.
解:原式=2x2-xy+10y2=16
C
A
25. 计算a+b+(a-b)的最后结果是( )
A.2a+2b B.2b
C.2a D.0
26. 计算5(2x-3)+4(3-2x)的结果为( )
A.2x-3 B.2x+9
C.8x-3 D.18x-3
27. 当x=5时,(x2-x)-(x2-2x+1)=( )
A.-14 B.4
C.-4 D.1
B
B
28. 若A=x2-2xy+y2,B=x2+2xy+y2,则4xy=( )
A.A+B B.B-A
C.A-B D.2A-2B
29. 减去-4a等于3a2-2a-1的多项式是( )
A.3a2-6a-1 B.5a2-1
C.3a2+2a-1 D.3a2+6a-1
30. 化简:(x2+y2)-3(x2-2y2)=_______________.
31. 多项式x2-x+5减去3x2-4的结果是________________.
32. 多项式______________与m2+m-2的和是m2-2m.
A
-2x2+7y2
-2x2-x+9
-3m+2
