1.1.2 空间向量的数量积运算 同步训练-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(含答案)
文档属性
| 名称 | 1.1.2 空间向量的数量积运算 同步训练-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 37.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:25:06 | ||
图片预览

文档简介
1.1.2 空间向量的数量积运算(同步训练)
1.设a,b,c是任意的非零向量,且它们互相不共线,则下列命题:
①(a·b)c-(c·a)b=0;②|a|-|b|<|a-b|;
③(a·b)c-(c·a)b不与c垂直;④(3a+2b)·(3a-2b)=9|a|2-4|b|2.
其中正确的有( )
A.①② B.②③ C.③④ D.②④
2.在空间四边形ABCD中,·+·+·=( )
A.0 B.1
C.2 D.3
3.在正四面体P-ABC中,棱长为1,且D为棱AB的中点,则·的值为( )
A.- B.
C.- D.
4.已知|a|=13,|b|=19,|a+b|=24,则|a-b|等于( )
A.22 B.48
C.28 D.32
5.设a,b,c为非零向量,则(a·b)·c( )
A.是三个向量的数量积 B.是与a共线的向量
C.是与c共线的向量 D.无意义
6.已知非零向量b在非零向量a方向上的投影为零,则向量a,b的关系是( )
A.a∥b B.a⊥b
C.a与b相交 D.a与b重合
7.已知|a|=3,|b|=4,a与b的夹角为135°,m=a+b,n=a+λb,若m⊥n,则λ=( )
A.-1 B.-
C.-2 D.1
8.(多选)(2021年邢台月考)下列关于数量积的运算正确的是( )
A.|a·b|=|a|·|b| B.|a-b|=
C.(a·b)·c=a·(b·c) D.(a+b)·c=a·c+b·c
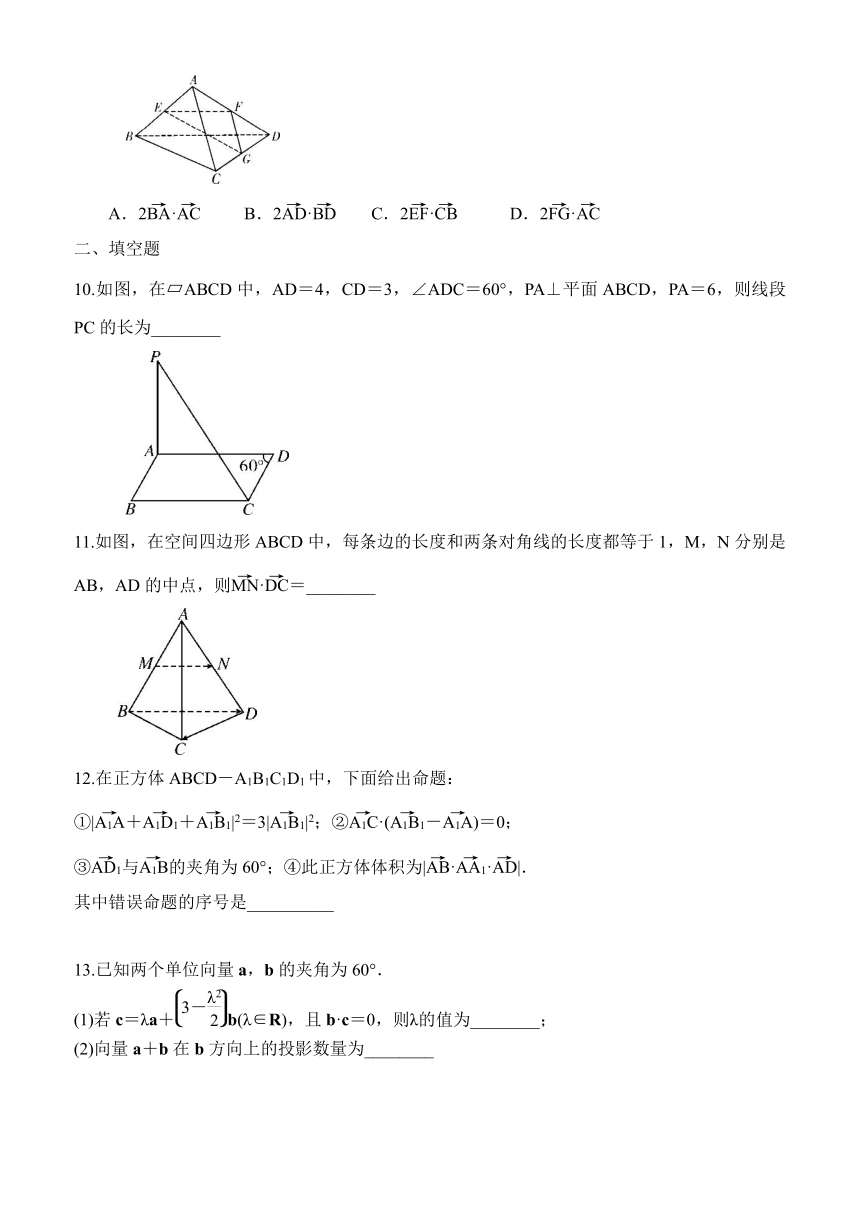
9.(多选)如图,在四面体A-BCD中,各棱长均为a,E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是( )
A.2· B.2· C.2· D.2·
二、填空题
10.如图,在 ABCD中,AD=4,CD=3,∠ADC=60°,PA⊥平面ABCD,PA=6,则线段PC的长为________
11.如图,在空间四边形ABCD中,每条边的长度和两条对角线的长度都等于1,M,N分别是AB,AD的中点,则·=________
12.在正方体ABCD-A1B1C1D1中,下面给出命题:
①|++|2=3||2;②·(-)=0;
③与的夹角为60°;④此正方体体积为|··|.
其中错误命题的序号是__________
13.已知两个单位向量a,b的夹角为60°.
(1)若c=λa+b(λ∈R),且b·c=0,则λ的值为________;
(2)向量a+b在b方向上的投影数量为________
三、解答题
14.如图,已知正四面体OABC的棱长为1,求:
(1)(+)·(+);(2)|++|.
15.如图,在平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=.设=a,=b,=c.
(1)试用a,b,c表示向量,;
(2)若∠A1AD=∠A1AB=120°,求直线AC与BD1所成的角.
参考答案:
一、选择题
1.D 2.A 3.D 4.A 5.C 6.B 7.B 8.BD 9.BD
二、填空题
10.答案:7 11.答案:- 12.答案:③④ 13.答案:(1)-2或3 (2)
三、解答题
14.解:(1)(+)·(+)=(+)·(-+-)=(+)·(+-2)=12+1×1×cos 60°-2×1×1×cos 60°+1×1×cos 60°+12-2×1×1×cos 60°=1.
(2)|++|==
==.
15.解:(1)由向量的加减运算法则知=+=a+b,=-=b+c-a.
(2)由题意知|a|=|b|=1,|c|=,〈a,b〉=90°,〈a,c〉=〈b,c〉=120°,
·=(a+b)·(b+c-a)=a·c-a2+b2+b·c=1··cos 120°-1+1+1·cos 120°=--=-.
因为||=.
||=====2,
所以cos〈,〉===-.所以〈,〉=120°,
即AC与BD1所成的角为60°.
1.设a,b,c是任意的非零向量,且它们互相不共线,则下列命题:
①(a·b)c-(c·a)b=0;②|a|-|b|<|a-b|;
③(a·b)c-(c·a)b不与c垂直;④(3a+2b)·(3a-2b)=9|a|2-4|b|2.
其中正确的有( )
A.①② B.②③ C.③④ D.②④
2.在空间四边形ABCD中,·+·+·=( )
A.0 B.1
C.2 D.3
3.在正四面体P-ABC中,棱长为1,且D为棱AB的中点,则·的值为( )
A.- B.
C.- D.
4.已知|a|=13,|b|=19,|a+b|=24,则|a-b|等于( )
A.22 B.48
C.28 D.32
5.设a,b,c为非零向量,则(a·b)·c( )
A.是三个向量的数量积 B.是与a共线的向量
C.是与c共线的向量 D.无意义
6.已知非零向量b在非零向量a方向上的投影为零,则向量a,b的关系是( )
A.a∥b B.a⊥b
C.a与b相交 D.a与b重合
7.已知|a|=3,|b|=4,a与b的夹角为135°,m=a+b,n=a+λb,若m⊥n,则λ=( )
A.-1 B.-
C.-2 D.1
8.(多选)(2021年邢台月考)下列关于数量积的运算正确的是( )
A.|a·b|=|a|·|b| B.|a-b|=
C.(a·b)·c=a·(b·c) D.(a+b)·c=a·c+b·c
9.(多选)如图,在四面体A-BCD中,各棱长均为a,E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是( )
A.2· B.2· C.2· D.2·
二、填空题
10.如图,在 ABCD中,AD=4,CD=3,∠ADC=60°,PA⊥平面ABCD,PA=6,则线段PC的长为________
11.如图,在空间四边形ABCD中,每条边的长度和两条对角线的长度都等于1,M,N分别是AB,AD的中点,则·=________
12.在正方体ABCD-A1B1C1D1中,下面给出命题:
①|++|2=3||2;②·(-)=0;
③与的夹角为60°;④此正方体体积为|··|.
其中错误命题的序号是__________
13.已知两个单位向量a,b的夹角为60°.
(1)若c=λa+b(λ∈R),且b·c=0,则λ的值为________;
(2)向量a+b在b方向上的投影数量为________
三、解答题
14.如图,已知正四面体OABC的棱长为1,求:
(1)(+)·(+);(2)|++|.
15.如图,在平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=.设=a,=b,=c.
(1)试用a,b,c表示向量,;
(2)若∠A1AD=∠A1AB=120°,求直线AC与BD1所成的角.
参考答案:
一、选择题
1.D 2.A 3.D 4.A 5.C 6.B 7.B 8.BD 9.BD
二、填空题
10.答案:7 11.答案:- 12.答案:③④ 13.答案:(1)-2或3 (2)
三、解答题
14.解:(1)(+)·(+)=(+)·(-+-)=(+)·(+-2)=12+1×1×cos 60°-2×1×1×cos 60°+1×1×cos 60°+12-2×1×1×cos 60°=1.
(2)|++|==
==.
15.解:(1)由向量的加减运算法则知=+=a+b,=-=b+c-a.
(2)由题意知|a|=|b|=1,|c|=,〈a,b〉=90°,〈a,c〉=〈b,c〉=120°,
·=(a+b)·(b+c-a)=a·c-a2+b2+b·c=1··cos 120°-1+1+1·cos 120°=--=-.
因为||=.
||=====2,
所以cos〈,〉===-.所以〈,〉=120°,
即AC与BD1所成的角为60°.
