人教版九年级上册24.3 正多边形和圆 课件(共21张PPT)
文档属性
| 名称 | 人教版九年级上册24.3 正多边形和圆 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 632.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
24.3 正多边形和圆
第二十四章 圆
24.3 正多边形和圆
情景导入
生活中的正多边形图案
获取新知
知识点一:圆的内接正多边形
1. 你还记得什么样的图形是正多边形吗?
各边相等,各角也相等的多边形叫正多边形(同时满足)
2.正多边形有哪些性质?
正多边形的各边相等,
正多边形的各角相等
思考
你知道正多边形与圆的关系吗?
问题1 怎样把一个圆进行四等分?
问题2 依次连接各等分点,得到一个什么图形?
A
B
C
D
·
O
⌒
BC;
BC+CD+DE=
⌒
⌒
⌒
①
=
③ ∠A ∠E;
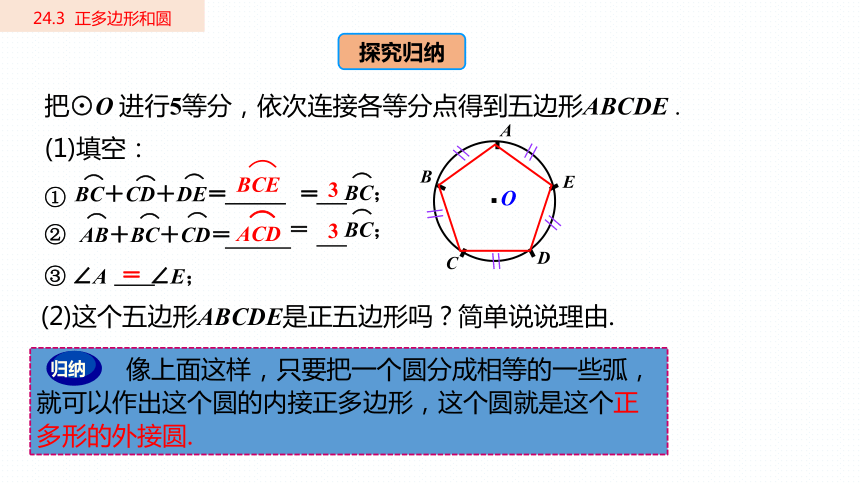
把⊙O 进行5等分,依次连接各等分点得到五边形ABCDE .
(1)填空:
·
A
O
E
D
C
B
⌒
BCE
⌒
BC;
AB+BC+CD=
⌒
⌒
⌒
②
=
3
3
=
ACD
⌒
(2)这个五边形ABCDE是正五边形吗?简单说说理由.
像上面这样,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多形的外接圆.
归纳
探究归纳
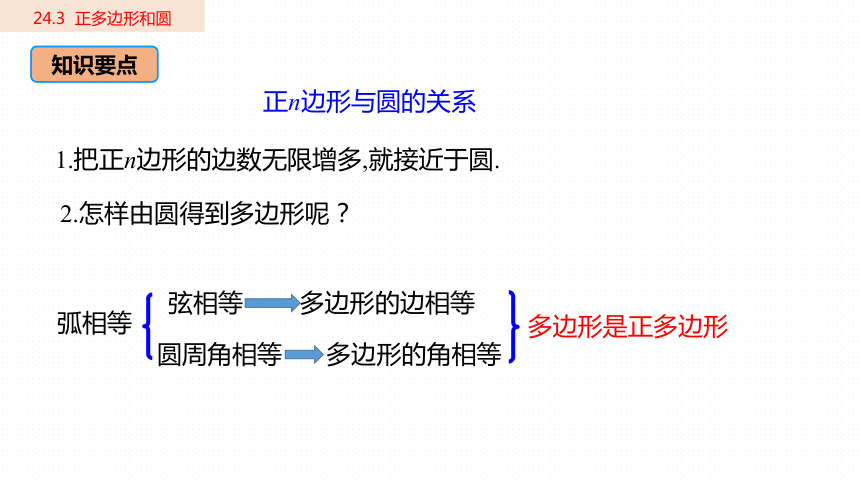
正n边形与圆的关系
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢?
弧相等
弦相等 多边形的边相等
圆周角相等 多边形的角相等
多边形是正多边形
知识要点
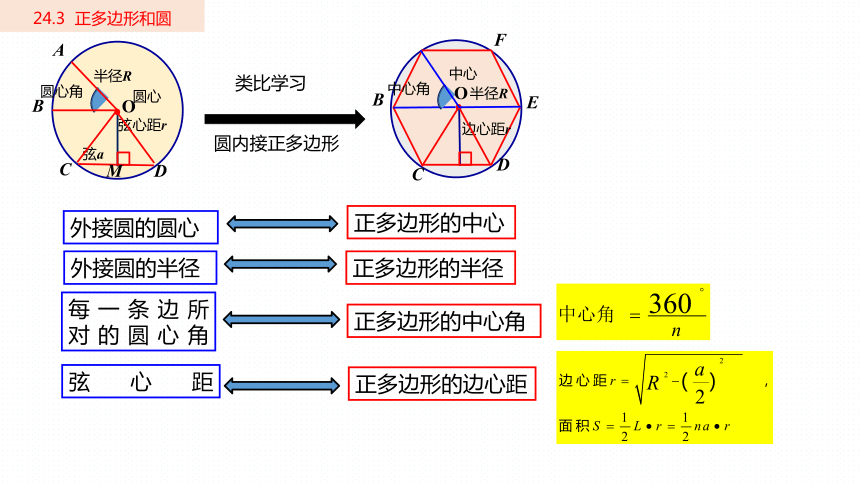
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
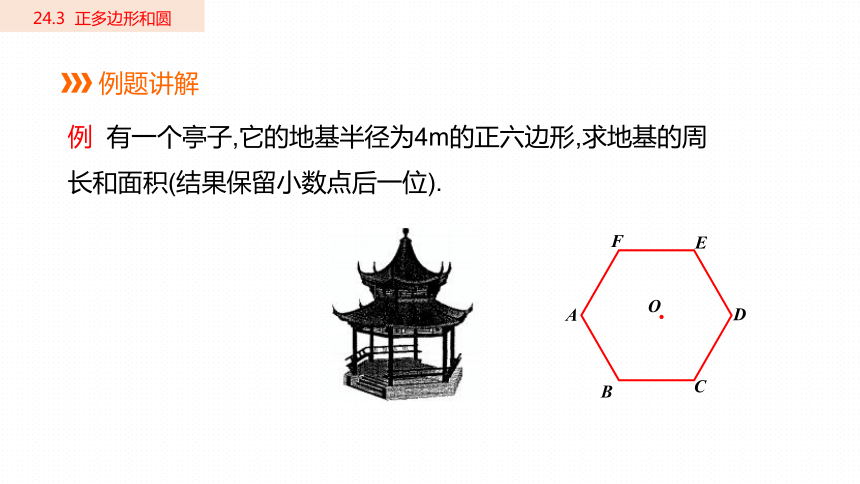
例题讲解
例 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).
O
A
B
C
D
E
F
解:如图,连接OB,OC.因为六边形ABCDEF是正六边形,所以它的中心角等于 =60°,△OBC是等边三角形,
从而正六边形的边长等于它的半径.
作OP⊥BC,垂足为P.
在Rt△OPC中,OC=4 m,
PC= =2(m),利用勾股定理,
可得边心距r=
亭子地基的面积S=
O
A
B
C
D
E
F
R
r
P
因此,亭子地基的周长l=6×4=24(m).
获取新知
知识点二:正多边形的作图
已知⊙O的半径为R,求作⊙O的内接正六边形.
分析:因为正六边形每条边所对的圆心角为 ,
所以正六边形的边长与圆的半径 .
因此,在半径为R的圆上依次截取长度为 的弦,
即可将圆六等分.
60
相等
R
作法:(1)在⊙O的任意取一点A;
(2)用量角器量出∠AOB=60°;
(3)在圆上依次截取六段与 相等的弧,交⊙O与点C、点D、 点E、点F;
(4)依次连接AB、BC、CD、DE、EF、FA,便得到正六边形ABCDEF.
O
F
A
B
D
E
·
C
60°
⌒
AB
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
作法:(1)作⊙O的任意一条直径FC;
(2)分别以F,C为圆心,以R为半径作弧,与⊙O
交于点E,A和D,B;
(3)依次连接AB、BC、CD、DE、EF、FA,便
得到正六边形ABCDEF.
. O
F
C
A
B
D
E
你能说明这么作图的依据吗?连续的在圆上截取半径为R的弦有什么问题吗?
对于一些特殊的正多边形,还可以利用尺规来作.
例如正六边形还可以按如下方法作出:
用量角器等分圆:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形.采用“先用量角器画一个 的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”.
这种方法简便,且可以画任意正多边形、误差小.
方法归纳
用尺规等分圆:
用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差.
例题讲解
例2 用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
你能简单说明下如何用尺规做出两条垂直的直径吗?
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
1.一元钱硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大不能超过( )
A.12 mm B.12 mm
C.6 mm D.6 mm
A
随堂演练
2. 如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
C
3、 若正六边形的边长为1,那么正六边形的中心角是______°,半径是_______,边心距是_______,它的每一个内角是_______.
60
1
120°
4.用尺规作图(不要求写作法和证明,但要保留作图痕迹).
(1)如图,已知正五边形ABCDE,求作它的中心O.
(2)如图,已知☉O,求作☉O的内接正八边形.
解:(1)如图①,点O即为所求.
(2)如图②,八边形ABCDEFGH即为所求.
课堂小结
圆内接正多边形
正多边形和圆的关系
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正n边形各顶点等分其外接圆.
24.3 正多边形和圆
第二十四章 圆
24.3 正多边形和圆
情景导入
生活中的正多边形图案
获取新知
知识点一:圆的内接正多边形
1. 你还记得什么样的图形是正多边形吗?
各边相等,各角也相等的多边形叫正多边形(同时满足)
2.正多边形有哪些性质?
正多边形的各边相等,
正多边形的各角相等
思考
你知道正多边形与圆的关系吗?
问题1 怎样把一个圆进行四等分?
问题2 依次连接各等分点,得到一个什么图形?
A
B
C
D
·
O
⌒
BC;
BC+CD+DE=
⌒
⌒
⌒
①
=
③ ∠A ∠E;
把⊙O 进行5等分,依次连接各等分点得到五边形ABCDE .
(1)填空:
·
A
O
E
D
C
B
⌒
BCE
⌒
BC;
AB+BC+CD=
⌒
⌒
⌒
②
=
3
3
=
ACD
⌒
(2)这个五边形ABCDE是正五边形吗?简单说说理由.
像上面这样,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多形的外接圆.
归纳
探究归纳
正n边形与圆的关系
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢?
弧相等
弦相等 多边形的边相等
圆周角相等 多边形的角相等
多边形是正多边形
知识要点
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
例题讲解
例 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).
O
A
B
C
D
E
F
解:如图,连接OB,OC.因为六边形ABCDEF是正六边形,所以它的中心角等于 =60°,△OBC是等边三角形,
从而正六边形的边长等于它的半径.
作OP⊥BC,垂足为P.
在Rt△OPC中,OC=4 m,
PC= =2(m),利用勾股定理,
可得边心距r=
亭子地基的面积S=
O
A
B
C
D
E
F
R
r
P
因此,亭子地基的周长l=6×4=24(m).
获取新知
知识点二:正多边形的作图
已知⊙O的半径为R,求作⊙O的内接正六边形.
分析:因为正六边形每条边所对的圆心角为 ,
所以正六边形的边长与圆的半径 .
因此,在半径为R的圆上依次截取长度为 的弦,
即可将圆六等分.
60
相等
R
作法:(1)在⊙O的任意取一点A;
(2)用量角器量出∠AOB=60°;
(3)在圆上依次截取六段与 相等的弧,交⊙O与点C、点D、 点E、点F;
(4)依次连接AB、BC、CD、DE、EF、FA,便得到正六边形ABCDEF.
O
F
A
B
D
E
·
C
60°
⌒
AB
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
作法:(1)作⊙O的任意一条直径FC;
(2)分别以F,C为圆心,以R为半径作弧,与⊙O
交于点E,A和D,B;
(3)依次连接AB、BC、CD、DE、EF、FA,便
得到正六边形ABCDEF.
. O
F
C
A
B
D
E
你能说明这么作图的依据吗?连续的在圆上截取半径为R的弦有什么问题吗?
对于一些特殊的正多边形,还可以利用尺规来作.
例如正六边形还可以按如下方法作出:
用量角器等分圆:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形.采用“先用量角器画一个 的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”.
这种方法简便,且可以画任意正多边形、误差小.
方法归纳
用尺规等分圆:
用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差.
例题讲解
例2 用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
你能简单说明下如何用尺规做出两条垂直的直径吗?
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
1.一元钱硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大不能超过( )
A.12 mm B.12 mm
C.6 mm D.6 mm
A
随堂演练
2. 如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
C
3、 若正六边形的边长为1,那么正六边形的中心角是______°,半径是_______,边心距是_______,它的每一个内角是_______.
60
1
120°
4.用尺规作图(不要求写作法和证明,但要保留作图痕迹).
(1)如图,已知正五边形ABCDE,求作它的中心O.
(2)如图,已知☉O,求作☉O的内接正八边形.
解:(1)如图①,点O即为所求.
(2)如图②,八边形ABCDEFGH即为所求.
课堂小结
圆内接正多边形
正多边形和圆的关系
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正n边形各顶点等分其外接圆.
同课章节目录
