人教版八年级数学上册11.1.2 三角形的高、中线与角平分线 课堂提升训练试卷(word版 有答案)
文档属性
| 名称 | 人教版八年级数学上册11.1.2 三角形的高、中线与角平分线 课堂提升训练试卷(word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 147.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 10:42:41 | ||
图片预览

文档简介
11.1.2 三角形的高、中线与角平分线 课堂提升训练试卷
一、选择题
1.将三角形面积平分的是三角形的( )
A.角平分线 B.高 C.中线 D.外角平分线
2.如图,点 和点 分别为 中 、 的中点, ,则 ( )
A. B. C. D.
3.如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )
A.4 B.8 C.12 D.16
4.下列说法中错误的是
A.三角形的中线、角平分线、高线都是线段
B.任意三角形的外角和都是360°
C.有一个内角是直角的三角形是直角三角形
D.三角形的一个外角大于任何一个内角
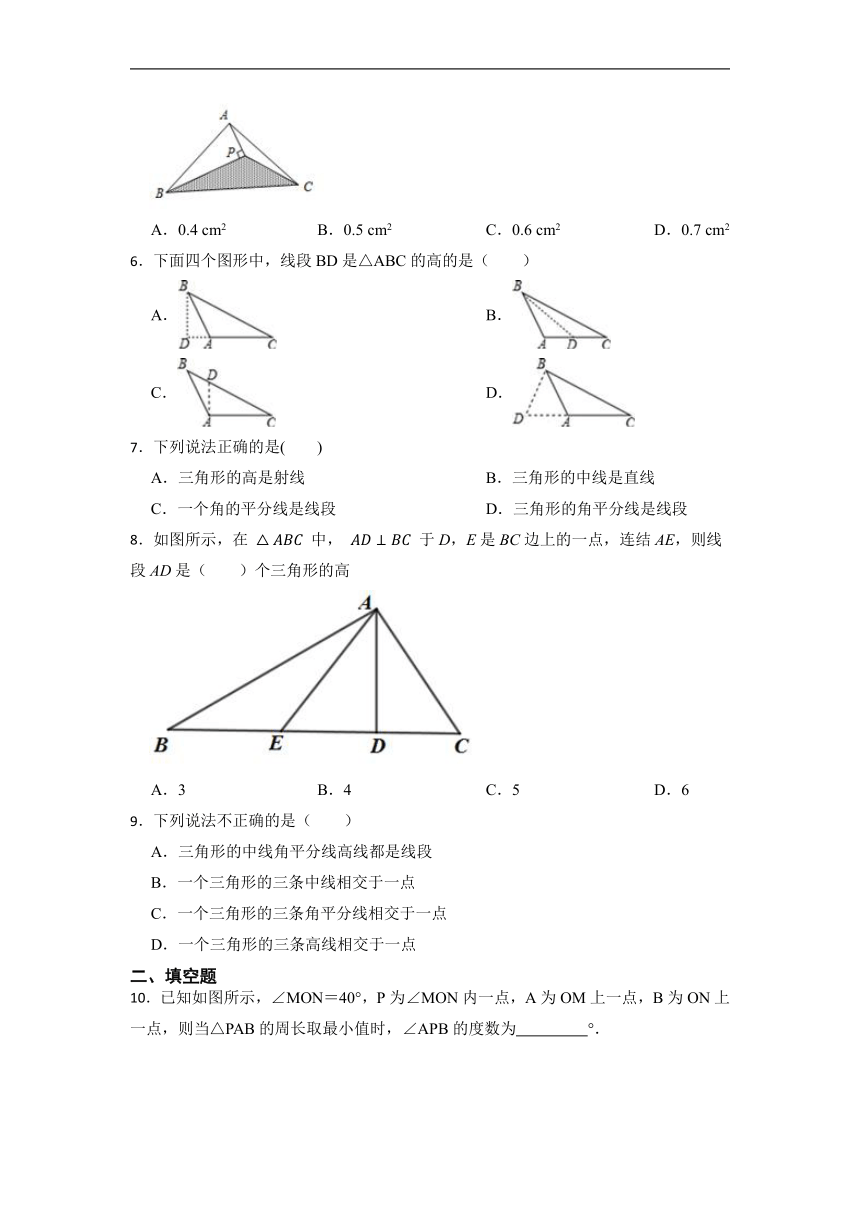
5.如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
A.0.4 cm2 B.0.5 cm2 C.0.6 cm2 D.0.7 cm2
6.下面四个图形中,线段BD是△ABC的高的是( )
A. B.
C. D.
7.下列说法正确的是( )
A.三角形的高是射线 B.三角形的中线是直线
C.一个角的平分线是线段 D.三角形的角平分线是线段
8.如图所示,在 中, 于D,E是BC边上的一点,连结AE,则线段AD是( )个三角形的高
A.3 B.4 C.5 D.6
9.下列说法不正确的是( )
A.三角形的中线角平分线高线都是线段
B.一个三角形的三条中线相交于一点
C.一个三角形的三条角平分线相交于一点
D.一个三角形的三条高线相交于一点
二、填空题
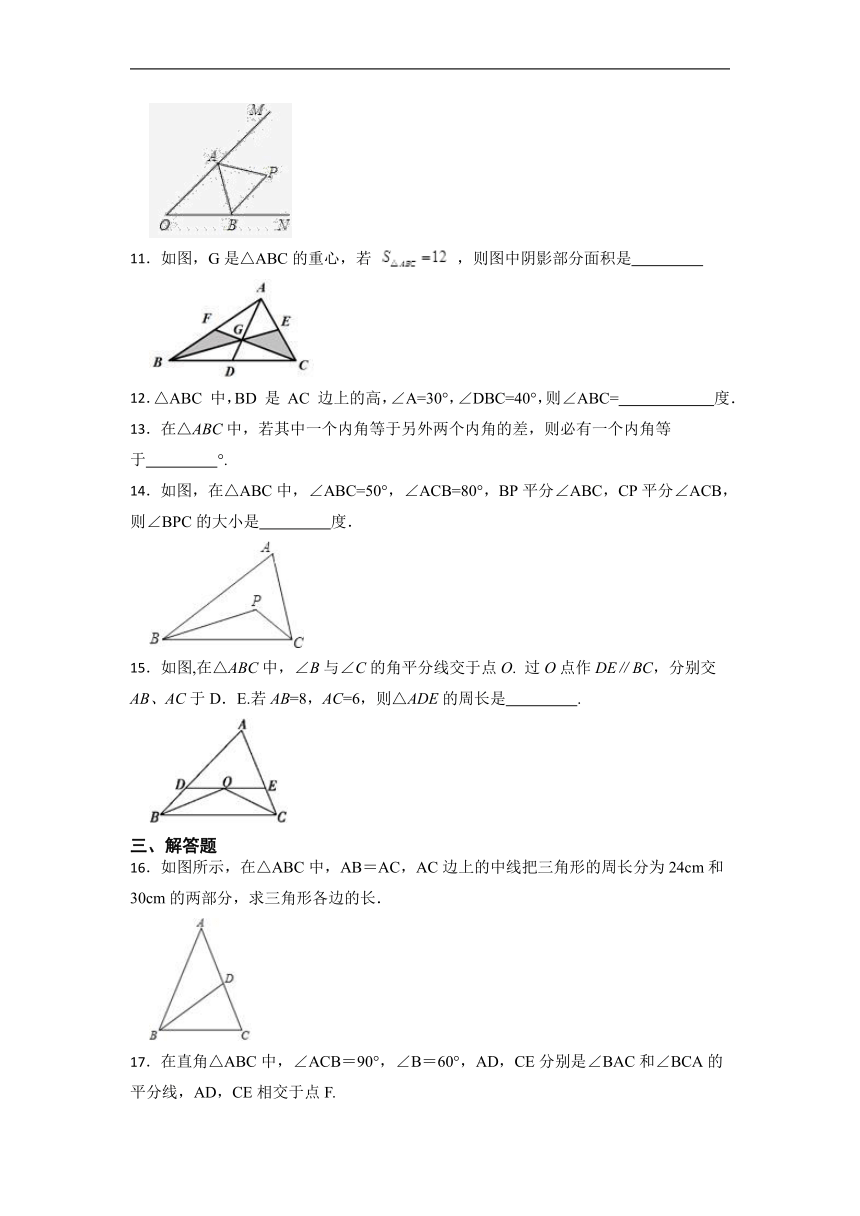
10.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为 °.
11.如图,G是△ABC的重心,若 ,则图中阴影部分面积是
12.△ABC 中,BD 是 AC 边上的高,∠A=30°,∠DBC=40°,则∠ABC= 度.
13.在△ABC中,若其中一个内角等于另外两个内角的差,则必有一个内角等于 °.
14.如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是 度.
15.如图,在△ABC中,∠B与∠C的角平分线交于点O. 过O点作DE∥BC,分别交AB、AC于D.E.若AB=8,AC=6,则△ADE的周长是 .
三、解答题
16.如图所示,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24cm和30cm的两部分,求三角形各边的长.
17.在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
求∠EFD的度数;
18.如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中,画出△ABD的BD边上的中线;
(2)在图2中,若BA=BD,画出△ABD的AD边上的高.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】D
9.【答案】D
10.【答案】100
11.【答案】4
12.【答案】100或20
13.【答案】90
14.【答案】115
15.【答案】14
16.【答案】解:根据题意画出图形,如下图,
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为24,则2x+x=24,解得x=8,
则x+y=30,即8+y=30,解得y=22,
则等腰三角形的腰长为16厘米,底边长为22厘米,能够成三角形;
若AB+AD的长为30,则2x+x=30,解得x=10,
则x+y=24,即10+y=24,解得y=14;
则腰长为20cm,底长为14cm,能够成三角形.
17.【答案】解:∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=∠BAC=15°,∠FCA=∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
18.【答案】(1)解:如图1所示,AF即为所求:
(2)解:如图2所示,BH即为所求.
一、选择题
1.将三角形面积平分的是三角形的( )
A.角平分线 B.高 C.中线 D.外角平分线
2.如图,点 和点 分别为 中 、 的中点, ,则 ( )
A. B. C. D.
3.如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )
A.4 B.8 C.12 D.16
4.下列说法中错误的是
A.三角形的中线、角平分线、高线都是线段
B.任意三角形的外角和都是360°
C.有一个内角是直角的三角形是直角三角形
D.三角形的一个外角大于任何一个内角
5.如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
A.0.4 cm2 B.0.5 cm2 C.0.6 cm2 D.0.7 cm2
6.下面四个图形中,线段BD是△ABC的高的是( )
A. B.
C. D.
7.下列说法正确的是( )
A.三角形的高是射线 B.三角形的中线是直线
C.一个角的平分线是线段 D.三角形的角平分线是线段
8.如图所示,在 中, 于D,E是BC边上的一点,连结AE,则线段AD是( )个三角形的高
A.3 B.4 C.5 D.6
9.下列说法不正确的是( )
A.三角形的中线角平分线高线都是线段
B.一个三角形的三条中线相交于一点
C.一个三角形的三条角平分线相交于一点
D.一个三角形的三条高线相交于一点
二、填空题
10.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为 °.
11.如图,G是△ABC的重心,若 ,则图中阴影部分面积是
12.△ABC 中,BD 是 AC 边上的高,∠A=30°,∠DBC=40°,则∠ABC= 度.
13.在△ABC中,若其中一个内角等于另外两个内角的差,则必有一个内角等于 °.
14.如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是 度.
15.如图,在△ABC中,∠B与∠C的角平分线交于点O. 过O点作DE∥BC,分别交AB、AC于D.E.若AB=8,AC=6,则△ADE的周长是 .
三、解答题
16.如图所示,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24cm和30cm的两部分,求三角形各边的长.
17.在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
求∠EFD的度数;
18.如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中,画出△ABD的BD边上的中线;
(2)在图2中,若BA=BD,画出△ABD的AD边上的高.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】D
9.【答案】D
10.【答案】100
11.【答案】4
12.【答案】100或20
13.【答案】90
14.【答案】115
15.【答案】14
16.【答案】解:根据题意画出图形,如下图,
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为24,则2x+x=24,解得x=8,
则x+y=30,即8+y=30,解得y=22,
则等腰三角形的腰长为16厘米,底边长为22厘米,能够成三角形;
若AB+AD的长为30,则2x+x=30,解得x=10,
则x+y=24,即10+y=24,解得y=14;
则腰长为20cm,底长为14cm,能够成三角形.
17.【答案】解:∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=∠BAC=15°,∠FCA=∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
18.【答案】(1)解:如图1所示,AF即为所求:
(2)解:如图2所示,BH即为所求.
