第二十三章 旋转达标测试卷(含答案)
图片预览


文档简介
旋转自我评估
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
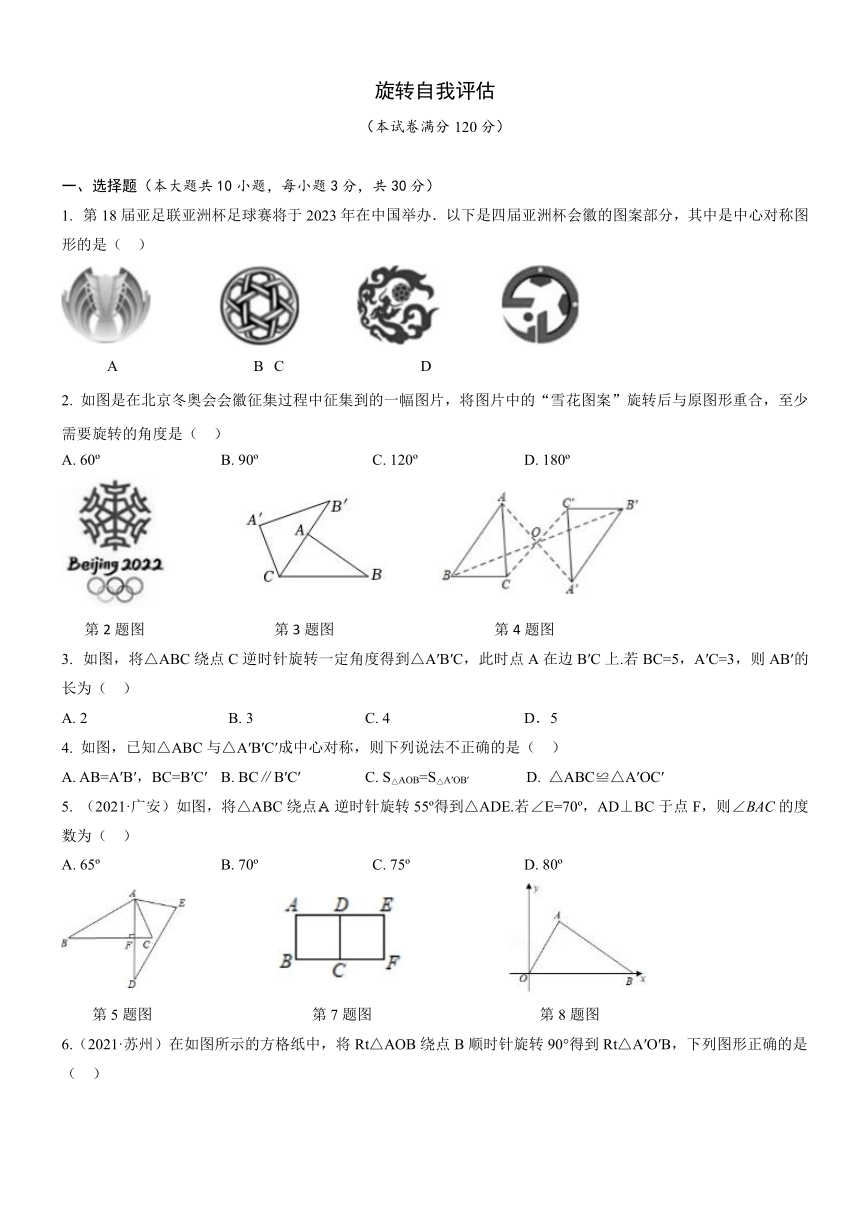
1. 第18届亚足联亚洲杯足球赛将于2023年在中国举办.以下是四届亚洲杯会徽的图案部分,其中是中心对称图形的是( )
A B C D
2. 如图是在北京冬奥会会徽征集过程中征集到的一幅图片,将图片中的“雪花图案”旋转后与原图形重合,至少需要旋转的角度是( )
A. 60 B. 90 C. 120 D. 180
第2题图 第3题图 第4题图
3. 如图,将△ABC绕点C逆时针旋转一定角度得到△A′B′C,此时点A在边B′C上.若BC=5,A′C=3,则AB′的长为( )
A. 2 B. 3 C. 4 D.5
4. 如图,已知△ABC与△A′B′C′成中心对称,则下列说法不正确的是( )
A. AB=A′B′,BC=B′C′ B. BC∥B′C′ C. S△AOB=S△A′OB′ D. △ABC≌△A′OC′
5. (2021·广安)如图,将△ABC绕点逆时针旋转55 得到△ADE.若∠E=70 ,AD⊥BC于点F,则∠BAC的度数为( )
A. 65 B. 70 C. 75 D. 80
第5题图 第7题图 第8题图
6.(2021·苏州)在如图所示的方格纸中,将Rt△AOB绕点B顺时针旋转90°得到Rt△A′O′B,下列图形正确的是( )
A B C D 第6题图
7. 如图,正方形CDEF绕某点旋转与正方形ABCD重合,这样的点的个数为( )
A. 0 B. 1 C. 2 D. 3
8. 如图,在△AOB中,OA=4,OB=6,AB=.将△AOB绕原点O旋转90°得到△A′OB′,则旋转后点A的对应点A′的坐标是( )
A.(4,2)或(﹣4,2) B. 或
C. 或 D. 或
9. (2021·衢州)如图,将菱形ABCD绕点A逆时针旋转α得到菱形AB′C′D′,∠B=β.当AC平分∠B′AC′时,α与β满足的数量关系是( )
A. α=2β B. 2α=3β C. 4α+β=180 D. 3α+2β=180
第9题图 第10题图
10. 如图,矩形ABCD的顶点A,B在两坐标轴上,OA=OB=2,BC=.将矩形ABCD绕原点O顺时针每次旋转90°,则第2022次旋转后点C的坐标是( )
A.(3,-5) B.(-5,-3) C.(-3,5) D.(5,3)
二、填空题(本大题共6小题,每小题4分,共24分)
11. 已知点P(-2,3)关于y轴的对称点为Q(a,b),点Q关于原点的对称点为R(m,n),则m+n的值是___________.
12. 如图,一块等腰直角三角尺ABC,在水平桌面上绕点C顺时针旋转到△A′B′C的位置,使A,C,B′三点共线,那么旋转的角度为_________________.
第12题图 第13题图 第14题图 第15题图 第16题图
13. (2021 青海)如图所示的图案由三个叶片组成,绕点O旋转120°后可以与自身重合.若每个叶片的面积为4 cm2,∠AOB=120°,则图中阴影部分的面积之和为 cm2.
14. 如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转,在旋转过程中,当AE=BF时,∠AOE的度数是 .
15. (2021·上海)定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.如图,在平面内有一个正方形,边长为2,中心为点O,在正方形外有一点P,OP=2,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为____________.
16. 如图,在Rt△ABC中,两条直角边AC=8,BC=6,将△ACB绕AC的中点M旋转一定角度得到△DFE,点F正好落在AB边上,DE与AB交于点G,则AG的长为_____________.
三、解答题(本大题共8小题,共66分)
17.(6分)(2021·黑龙江)如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,△ABO的三个顶点分别为A(-1,3),B(-4,3),O(0,0).
(1)画出△ABO关于原点对称的△A1B1O,并写出点B1的坐标;
(2)画出△ABO绕点顺时针旋转后得到的△A2B2O,并写出点B2的坐标.
第17题图 第18题图 第19题图
18.(6分)如图,四边形ABCD是正方形,△ADE旋转后能与△ABF重合.
(1)直接写出旋转中心和旋转角的度数;
(2)若AD=4,DE=1,连接EF,求EF的长.
19.(6分)如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°.
(1)求证:∠EAB=∠FAC;
(2)△ABC可以经过图形的变换得到△AEF,请描述这个变换;
(3)求∠AMB的度数.
20.(8分)对于平面直角坐标系xOy中的图形M和点P,给出如下定义:将图形M绕点P顺时针旋转90°得到图形N,图形N称为图形M关于点P的“垂直图形”.例如,如图所示点D为点C关于点P的“垂直图形”.
(1)点A关于原点O的“垂直图形”为点B.
①若点A的坐标为(0,2),则点B的坐标为_____________;
②若点B的坐标为(2,1),则点A的坐标为 _____________.
(2)已知E(-3,3),F(a,0),点E关于点F的“垂直图形”记为E',求点E'的坐标.(用含a的式子表示)
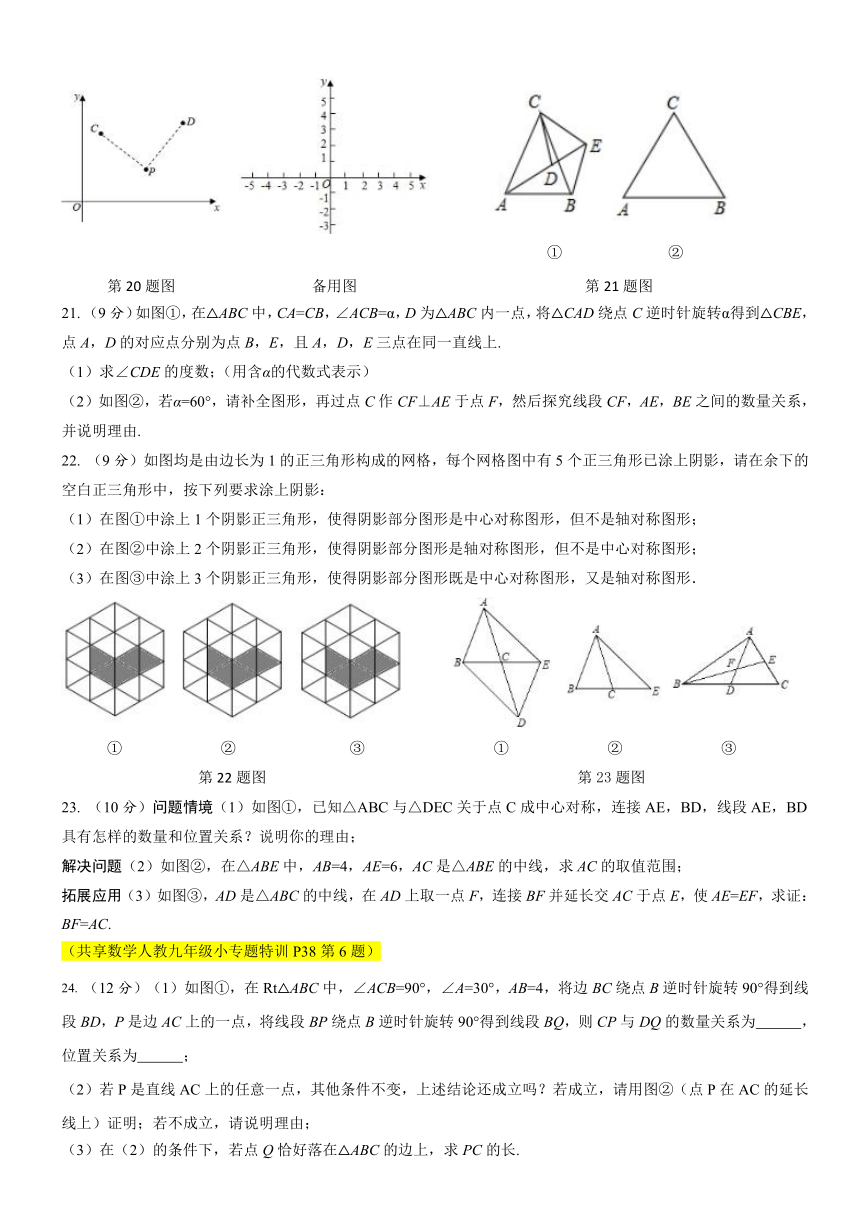
① ② 第20题图 备用图 第21题图
21. (9分)如图①,在△ABC中,CA=CB,∠ACB=α,D为△ABC内一点,将△CAD绕点C逆时针旋转α得到△CBE,点A,D的对应点分别为点B,E,且A,D,E三点在同一直线上.
(1)求∠CDE的度数;(用含α的代数式表示)
(2)如图②,若α=60°,请补全图形,再过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并说明理由.
22. (9分)如图均是由边长为1的正三角形构成的网格,每个网格图中有5个正三角形已涂上阴影,请在余下的空白正三角形中,按下列要求涂上阴影:
(1)在图①中涂上1个阴影正三角形,使得阴影部分图形是中心对称图形,但不是轴对称图形;
(2)在图②中涂上2个阴影正三角形,使得阴影部分图形是轴对称图形,但不是中心对称图形;
(3)在图③中涂上3个阴影正三角形,使得阴影部分图形既是中心对称图形,又是轴对称图形.
① ② ③ ① ② ③
第22题图 第23题图
23. (10分)问题情境(1)如图①,已知△ABC与△DEC关于点C成中心对称,连接AE,BD,线段AE,BD具有怎样的数量和位置关系?说明你的理由;
解决问题(2)如图②,在△ABE中,AB=4,AE=6,AC是△ABE的中线,求AC的取值范围;
拓展应用(3)如图③,AD是△ABC的中线,在AD上取一点F,连接BF并延长交AC于点E,使AE=EF,求证:BF=AC.
(共享数学人教九年级小专题特训P38第6题)
24. (12分)(1)如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,将边BC绕点B逆时针旋转90°得到线段BD,P是边AC上的一点,将线段BP绕点B逆时针旋转90°得到线段BQ,则CP与DQ的数量关系为 ,位置关系为 ;
(2)若P是直线AC上的任意一点,其他条件不变,上述结论还成立吗?若成立,请用图②(点P在AC的延长线上)证明;若不成立,请说明理由;
(3)在(2)的条件下,若点Q恰好落在△ABC的边上,求PC的长.
① ②
第24题图
(参考答案见答案页第2期)
题报第③期 旋转自我评估参考答案
答案详解
16. 解析:连接CF.因为AC=8,BC=6,所以AB===10.因为M是AC的中点,所以AM=MC=4.由旋转的性质,知∠A=∠D,DM=AM,CM=MF,DE=AB=10,所以AM=MF=CM.所以∠AFC=90°.因为AB·CF=AC·BC,所以CF=.所以AF==.因为∠A=∠D,∠A=∠AFM,所以∠D=∠AFM.又因为∠DFE=90°,所以DG=GF,∠E=∠GFE.所以GF=GE.所以GF=GD=GE=5.所以AG=AF-GF=-5=.
三、17.(1)图略,B1(4,-3). (2)图略,B2(3,4).
18. 解:(1)旋转中心为点A,旋转角的度数是90°.
(2)因为四边形ABCD是正方形,所以∠D=90°.所以AE===.
由旋转的性质,知AF=AE=,∠EAF=90°,所以EF=.
19.(1)证明:因为AB=AE,∠B=∠E,BC=EF,所以△ABC≌△AEF.
所以∠BAC=∠EAF.所以∠BAC﹣∠BAF=∠EAF﹣∠BAF.所以∠FAC=∠EAB=25°.
(2)解:将△ABC绕点A顺时针旋转25°得到△AEF.
(3)解:由(1)易得∠C=∠F=57°,∠FAC=∠EAB=25°,所以∠AMB=∠C+∠FAC=57°+25°=82°.
20. 解:(1)①(2,0) ②(-1,2)
(2)过点E作EH⊥x轴于点H,过点E′作E′K⊥x轴于点K,如图所示.
因为∠EHF=∠EFE′=∠E′KF=90°,所以∠EFH+∠E=90°,∠EFH+∠E′FK=90°.所以∠E=∠E′FK.
在△EHF和△FKE′中,∠EHF=∠FKE′,∠E=∠E′FK,EF=FE′,所以△EHF≌△FKE′(AAS).所以EH=FK=3,FH=KE′=a+3.所以OK=a+3.所以E′(a+3,a+3).
第20题图
21. 解:(1)由旋转的性质,得△BCE≌△ACD,所以CE=CD,∠BCE=∠ACD.所以∠CDE=∠CED,∠BCE+∠BCD=∠ACD+∠BCD,即∠DCE=∠ACB=α.所以∠CDE==.
(2)AE=BE+CF.
理由:补全图形,如图所示.因为将△CAD绕点C逆时针旋转60°得到△CBE,所以△CAD≌△CBE.所以AD=BE,CD=CE,∠DCE=60°.所以△CDE是等边三角形.
因为CF⊥DE,所以DF=EF=CD.所以CF==CD,即CD=DE=CF.
因为AE=AD+DE,所以AE=BE+CF.
① ② ③
第21题图 第22题图
22. 解:(1)如图①所示. (2)给出示例如图②所示(答案不唯一). (3)如图③所示.
23. 解:(1)AE∥BD且AE=BD.理由:因为△ABC与△DEC关于点C成中心对称,所以AC=CD,BC=CE.所以四边形ABDE是平行四边形.所以AE∥BD且AE=BD.
(2)作△DEB与△ABE关于点C成中心对称.由(1)易得四边形ABDE是平行四边形,所以BD=AE=6.
在△ABD中,AB=4,BD=6,所以BD﹣AB<AD<BD+AB.所以2<2AC<10.所以1<AC<5.
(3)因为AD是△ABC的中线,所以BD=CD.
作△BDH与△CDA关于点D成中心对称,则HD=AD,BH=AC,∠H=∠CAD.
因为AE=EF,所以∠EAF=∠AFE.因为∠AFE=∠BFH,所以∠H=∠BFH.所以BF=BH.所以AC=BF.
(共享数学人教九年级小专题特训参考答案P22第6题答案)
24. 解:(1)CP=DQ CP⊥DQ
(2)成立.证明:如图①,延长DQ交AC于点H.
因为将边BC绕点B旋转90°得到线段BD,所以BD=BC,∠DBC=90°. 因为将线段BP绕点B旋转90°得到线段BQ,所以BQ=BP,∠QBP=90°.所以∠QBP=∠DBC.所以∠DBQ=∠CBP.
所以△QBD≌△PBC.所以DQ=CP,∠D=∠BCP.
因为∠BCP+∠BCH=180°,所以∠D+∠BCH=180°.
因为∠D+∠BCH+∠DBC+∠CHD=360°,所以∠CHD=90°.所以CP⊥DQ.
① ② ③
第24题图
(3)当点Q在边AB上时,如图②,因为∠A=30°,∠PBQ=90°,所以∠P=60°,BC=AB=2.所以∠PBC=30°.所以BP=2PC.在Rt△PBC中,由勾股定理,得BP2=PC2+BC2,即4PC2=PC2+4.解得PC=±(负值舍去).
当点Q在边AC上时,如图③,因为BP=BQ,∠PBQ=90°,BC⊥AP,所以BC=PC=CQ=2.
综上所述,PC的长为或2.
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 第18届亚足联亚洲杯足球赛将于2023年在中国举办.以下是四届亚洲杯会徽的图案部分,其中是中心对称图形的是( )
A B C D
2. 如图是在北京冬奥会会徽征集过程中征集到的一幅图片,将图片中的“雪花图案”旋转后与原图形重合,至少需要旋转的角度是( )
A. 60 B. 90 C. 120 D. 180
第2题图 第3题图 第4题图
3. 如图,将△ABC绕点C逆时针旋转一定角度得到△A′B′C,此时点A在边B′C上.若BC=5,A′C=3,则AB′的长为( )
A. 2 B. 3 C. 4 D.5
4. 如图,已知△ABC与△A′B′C′成中心对称,则下列说法不正确的是( )
A. AB=A′B′,BC=B′C′ B. BC∥B′C′ C. S△AOB=S△A′OB′ D. △ABC≌△A′OC′
5. (2021·广安)如图,将△ABC绕点逆时针旋转55 得到△ADE.若∠E=70 ,AD⊥BC于点F,则∠BAC的度数为( )
A. 65 B. 70 C. 75 D. 80
第5题图 第7题图 第8题图
6.(2021·苏州)在如图所示的方格纸中,将Rt△AOB绕点B顺时针旋转90°得到Rt△A′O′B,下列图形正确的是( )
A B C D 第6题图
7. 如图,正方形CDEF绕某点旋转与正方形ABCD重合,这样的点的个数为( )
A. 0 B. 1 C. 2 D. 3
8. 如图,在△AOB中,OA=4,OB=6,AB=.将△AOB绕原点O旋转90°得到△A′OB′,则旋转后点A的对应点A′的坐标是( )
A.(4,2)或(﹣4,2) B. 或
C. 或 D. 或
9. (2021·衢州)如图,将菱形ABCD绕点A逆时针旋转α得到菱形AB′C′D′,∠B=β.当AC平分∠B′AC′时,α与β满足的数量关系是( )
A. α=2β B. 2α=3β C. 4α+β=180 D. 3α+2β=180
第9题图 第10题图
10. 如图,矩形ABCD的顶点A,B在两坐标轴上,OA=OB=2,BC=.将矩形ABCD绕原点O顺时针每次旋转90°,则第2022次旋转后点C的坐标是( )
A.(3,-5) B.(-5,-3) C.(-3,5) D.(5,3)
二、填空题(本大题共6小题,每小题4分,共24分)
11. 已知点P(-2,3)关于y轴的对称点为Q(a,b),点Q关于原点的对称点为R(m,n),则m+n的值是___________.
12. 如图,一块等腰直角三角尺ABC,在水平桌面上绕点C顺时针旋转到△A′B′C的位置,使A,C,B′三点共线,那么旋转的角度为_________________.
第12题图 第13题图 第14题图 第15题图 第16题图
13. (2021 青海)如图所示的图案由三个叶片组成,绕点O旋转120°后可以与自身重合.若每个叶片的面积为4 cm2,∠AOB=120°,则图中阴影部分的面积之和为 cm2.
14. 如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转,在旋转过程中,当AE=BF时,∠AOE的度数是 .
15. (2021·上海)定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.如图,在平面内有一个正方形,边长为2,中心为点O,在正方形外有一点P,OP=2,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为____________.
16. 如图,在Rt△ABC中,两条直角边AC=8,BC=6,将△ACB绕AC的中点M旋转一定角度得到△DFE,点F正好落在AB边上,DE与AB交于点G,则AG的长为_____________.
三、解答题(本大题共8小题,共66分)
17.(6分)(2021·黑龙江)如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,△ABO的三个顶点分别为A(-1,3),B(-4,3),O(0,0).
(1)画出△ABO关于原点对称的△A1B1O,并写出点B1的坐标;
(2)画出△ABO绕点顺时针旋转后得到的△A2B2O,并写出点B2的坐标.
第17题图 第18题图 第19题图
18.(6分)如图,四边形ABCD是正方形,△ADE旋转后能与△ABF重合.
(1)直接写出旋转中心和旋转角的度数;
(2)若AD=4,DE=1,连接EF,求EF的长.
19.(6分)如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°.
(1)求证:∠EAB=∠FAC;
(2)△ABC可以经过图形的变换得到△AEF,请描述这个变换;
(3)求∠AMB的度数.
20.(8分)对于平面直角坐标系xOy中的图形M和点P,给出如下定义:将图形M绕点P顺时针旋转90°得到图形N,图形N称为图形M关于点P的“垂直图形”.例如,如图所示点D为点C关于点P的“垂直图形”.
(1)点A关于原点O的“垂直图形”为点B.
①若点A的坐标为(0,2),则点B的坐标为_____________;
②若点B的坐标为(2,1),则点A的坐标为 _____________.
(2)已知E(-3,3),F(a,0),点E关于点F的“垂直图形”记为E',求点E'的坐标.(用含a的式子表示)
① ② 第20题图 备用图 第21题图
21. (9分)如图①,在△ABC中,CA=CB,∠ACB=α,D为△ABC内一点,将△CAD绕点C逆时针旋转α得到△CBE,点A,D的对应点分别为点B,E,且A,D,E三点在同一直线上.
(1)求∠CDE的度数;(用含α的代数式表示)
(2)如图②,若α=60°,请补全图形,再过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并说明理由.
22. (9分)如图均是由边长为1的正三角形构成的网格,每个网格图中有5个正三角形已涂上阴影,请在余下的空白正三角形中,按下列要求涂上阴影:
(1)在图①中涂上1个阴影正三角形,使得阴影部分图形是中心对称图形,但不是轴对称图形;
(2)在图②中涂上2个阴影正三角形,使得阴影部分图形是轴对称图形,但不是中心对称图形;
(3)在图③中涂上3个阴影正三角形,使得阴影部分图形既是中心对称图形,又是轴对称图形.
① ② ③ ① ② ③
第22题图 第23题图
23. (10分)问题情境(1)如图①,已知△ABC与△DEC关于点C成中心对称,连接AE,BD,线段AE,BD具有怎样的数量和位置关系?说明你的理由;
解决问题(2)如图②,在△ABE中,AB=4,AE=6,AC是△ABE的中线,求AC的取值范围;
拓展应用(3)如图③,AD是△ABC的中线,在AD上取一点F,连接BF并延长交AC于点E,使AE=EF,求证:BF=AC.
(共享数学人教九年级小专题特训P38第6题)
24. (12分)(1)如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,将边BC绕点B逆时针旋转90°得到线段BD,P是边AC上的一点,将线段BP绕点B逆时针旋转90°得到线段BQ,则CP与DQ的数量关系为 ,位置关系为 ;
(2)若P是直线AC上的任意一点,其他条件不变,上述结论还成立吗?若成立,请用图②(点P在AC的延长线上)证明;若不成立,请说明理由;
(3)在(2)的条件下,若点Q恰好落在△ABC的边上,求PC的长.
① ②
第24题图
(参考答案见答案页第2期)
题报第③期 旋转自我评估参考答案
答案详解
16. 解析:连接CF.因为AC=8,BC=6,所以AB===10.因为M是AC的中点,所以AM=MC=4.由旋转的性质,知∠A=∠D,DM=AM,CM=MF,DE=AB=10,所以AM=MF=CM.所以∠AFC=90°.因为AB·CF=AC·BC,所以CF=.所以AF==.因为∠A=∠D,∠A=∠AFM,所以∠D=∠AFM.又因为∠DFE=90°,所以DG=GF,∠E=∠GFE.所以GF=GE.所以GF=GD=GE=5.所以AG=AF-GF=-5=.
三、17.(1)图略,B1(4,-3). (2)图略,B2(3,4).
18. 解:(1)旋转中心为点A,旋转角的度数是90°.
(2)因为四边形ABCD是正方形,所以∠D=90°.所以AE===.
由旋转的性质,知AF=AE=,∠EAF=90°,所以EF=.
19.(1)证明:因为AB=AE,∠B=∠E,BC=EF,所以△ABC≌△AEF.
所以∠BAC=∠EAF.所以∠BAC﹣∠BAF=∠EAF﹣∠BAF.所以∠FAC=∠EAB=25°.
(2)解:将△ABC绕点A顺时针旋转25°得到△AEF.
(3)解:由(1)易得∠C=∠F=57°,∠FAC=∠EAB=25°,所以∠AMB=∠C+∠FAC=57°+25°=82°.
20. 解:(1)①(2,0) ②(-1,2)
(2)过点E作EH⊥x轴于点H,过点E′作E′K⊥x轴于点K,如图所示.
因为∠EHF=∠EFE′=∠E′KF=90°,所以∠EFH+∠E=90°,∠EFH+∠E′FK=90°.所以∠E=∠E′FK.
在△EHF和△FKE′中,∠EHF=∠FKE′,∠E=∠E′FK,EF=FE′,所以△EHF≌△FKE′(AAS).所以EH=FK=3,FH=KE′=a+3.所以OK=a+3.所以E′(a+3,a+3).
第20题图
21. 解:(1)由旋转的性质,得△BCE≌△ACD,所以CE=CD,∠BCE=∠ACD.所以∠CDE=∠CED,∠BCE+∠BCD=∠ACD+∠BCD,即∠DCE=∠ACB=α.所以∠CDE==.
(2)AE=BE+CF.
理由:补全图形,如图所示.因为将△CAD绕点C逆时针旋转60°得到△CBE,所以△CAD≌△CBE.所以AD=BE,CD=CE,∠DCE=60°.所以△CDE是等边三角形.
因为CF⊥DE,所以DF=EF=CD.所以CF==CD,即CD=DE=CF.
因为AE=AD+DE,所以AE=BE+CF.
① ② ③
第21题图 第22题图
22. 解:(1)如图①所示. (2)给出示例如图②所示(答案不唯一). (3)如图③所示.
23. 解:(1)AE∥BD且AE=BD.理由:因为△ABC与△DEC关于点C成中心对称,所以AC=CD,BC=CE.所以四边形ABDE是平行四边形.所以AE∥BD且AE=BD.
(2)作△DEB与△ABE关于点C成中心对称.由(1)易得四边形ABDE是平行四边形,所以BD=AE=6.
在△ABD中,AB=4,BD=6,所以BD﹣AB<AD<BD+AB.所以2<2AC<10.所以1<AC<5.
(3)因为AD是△ABC的中线,所以BD=CD.
作△BDH与△CDA关于点D成中心对称,则HD=AD,BH=AC,∠H=∠CAD.
因为AE=EF,所以∠EAF=∠AFE.因为∠AFE=∠BFH,所以∠H=∠BFH.所以BF=BH.所以AC=BF.
(共享数学人教九年级小专题特训参考答案P22第6题答案)
24. 解:(1)CP=DQ CP⊥DQ
(2)成立.证明:如图①,延长DQ交AC于点H.
因为将边BC绕点B旋转90°得到线段BD,所以BD=BC,∠DBC=90°. 因为将线段BP绕点B旋转90°得到线段BQ,所以BQ=BP,∠QBP=90°.所以∠QBP=∠DBC.所以∠DBQ=∠CBP.
所以△QBD≌△PBC.所以DQ=CP,∠D=∠BCP.
因为∠BCP+∠BCH=180°,所以∠D+∠BCH=180°.
因为∠D+∠BCH+∠DBC+∠CHD=360°,所以∠CHD=90°.所以CP⊥DQ.
① ② ③
第24题图
(3)当点Q在边AB上时,如图②,因为∠A=30°,∠PBQ=90°,所以∠P=60°,BC=AB=2.所以∠PBC=30°.所以BP=2PC.在Rt△PBC中,由勾股定理,得BP2=PC2+BC2,即4PC2=PC2+4.解得PC=±(负值舍去).
当点Q在边AC上时,如图③,因为BP=BQ,∠PBQ=90°,BC⊥AP,所以BC=PC=CQ=2.
综上所述,PC的长为或2.
同课章节目录
