华东师大版七上数学 4.6.3余角和补角 课件(共14张PPT)
文档属性
| 名称 | 华东师大版七上数学 4.6.3余角和补角 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1006.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 11:23:07 | ||
图片预览



文档简介
(共14张PPT)
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6
华东师大版数学七年级上册
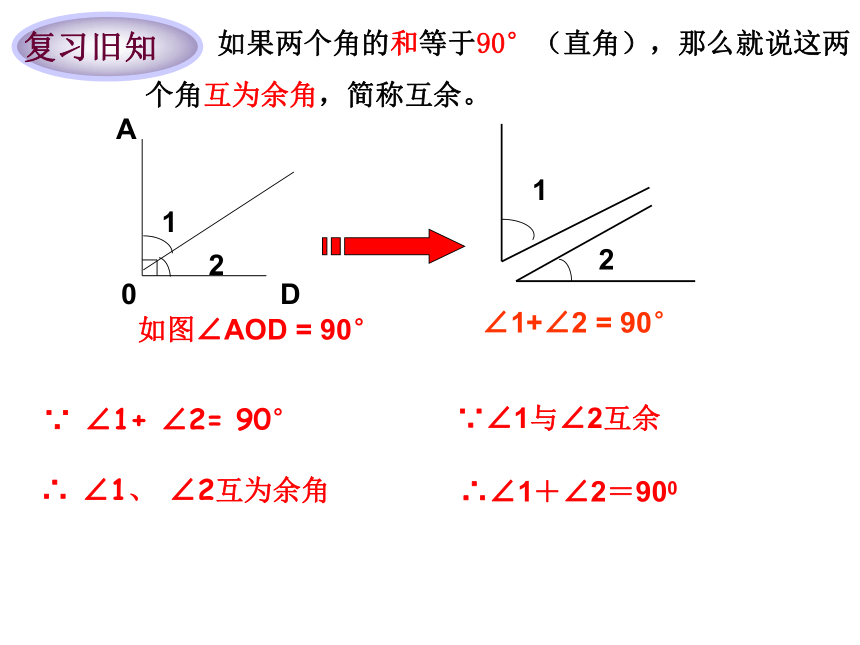
复习旧知
如果两个角的和等于90°(直角),那么就说这两个角互为余角,简称互余。
如图∠AOD = 90°
∠1+∠2 = 90°
0
A
D
1
2
1
2
∵ ∠1+ ∠2= 90°
∴ ∠1、 ∠2互为余角
∴∠1+∠2=900
∵∠1与∠2互余
利用三角尺画出∠1的余角
1
2
3
已知:∠2与∠3都是∠1的余角。
问: ∠2与∠3的大小关系。
解:∠2=∠3
A
O
B
C
D
探究一
∴ 90°-∠1 =90°- ∠1
即:________。
∵ ∠1 +∠2=90°,
∴ ∠2= 90 °-____;
∵ ∠1 +∠3=90°,
∴ ∠3= 90 °-_____;
∠1
∠1
∠2 =∠3
理由如下:
∵ ∠1 =∠3,
∴ 90°-∠1 =90°- ∠3
即:________。
∵ ∠1 +∠2=90°,
∴ ∠2= 90 °-____;
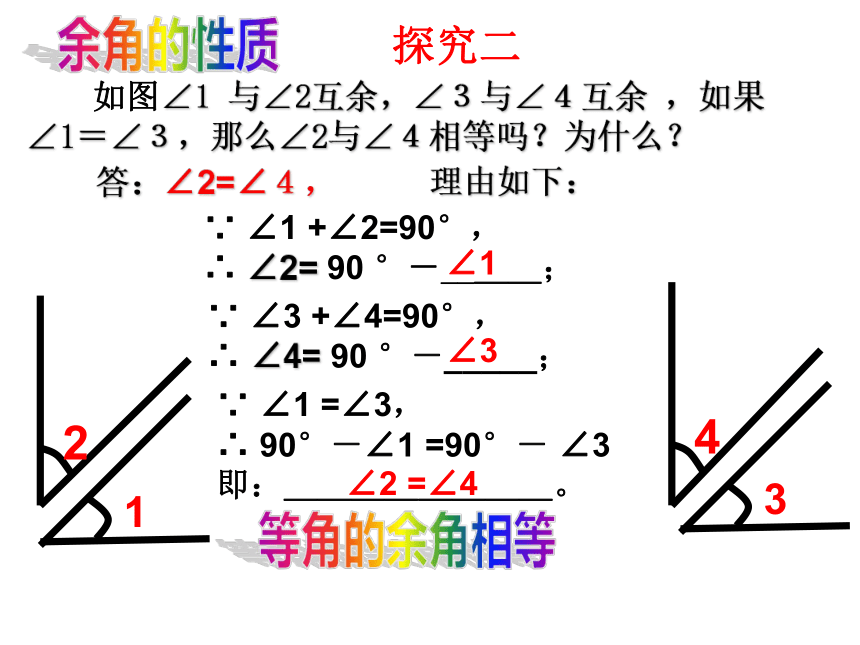
如图∠1 与∠2互余,∠3与∠4互余 ,如果
∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
3
4
答:∠2=∠4,
∠1
∠2 =∠4
理由如下:
∵ ∠3 +∠4=90°,
∴ ∠4= 90 °-_____;
∠3
探究二
几何语言:
∵ ∠1+ ∠ 2 = 900
∠ 1+ ∠ 3 = 900
∴ ∠ 2 = ∠ 3
(同角的余角相等)
几何语言:
∵ ∠1 + ∠ 2 = 900
∠ 3 + ∠ 4 = 900
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的余角相等)
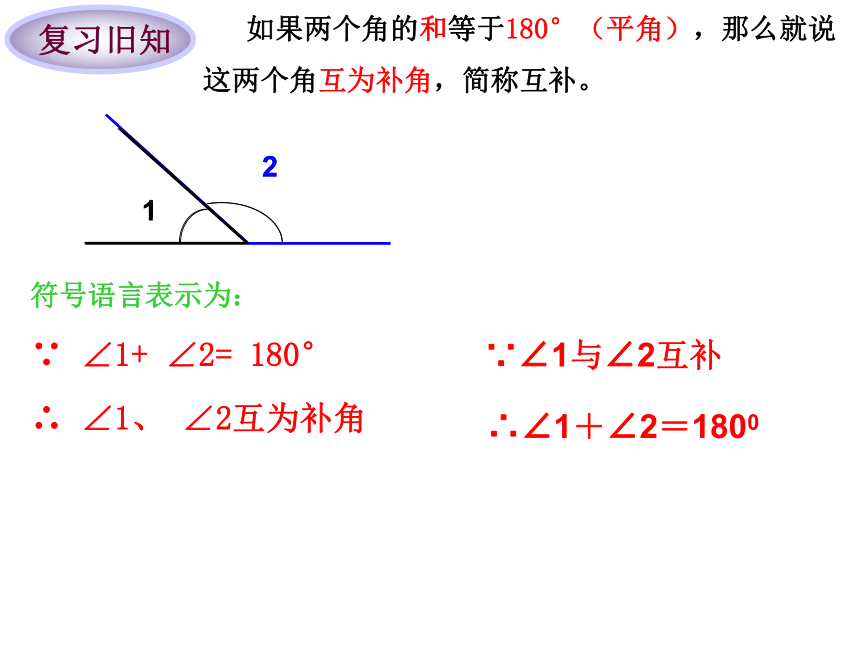
如果两个角的和等于180°(平角),那么就说
这两个角互为补角,简称互补。
符号语言表示为:
2
1
2
1
复习旧知
∵ ∠1+ ∠2= 180°
∴ ∠1、 ∠2互为补角
∴∠1+∠2=1800
∵∠1与∠2互补
B
A
O
C
O
A
B
1
2
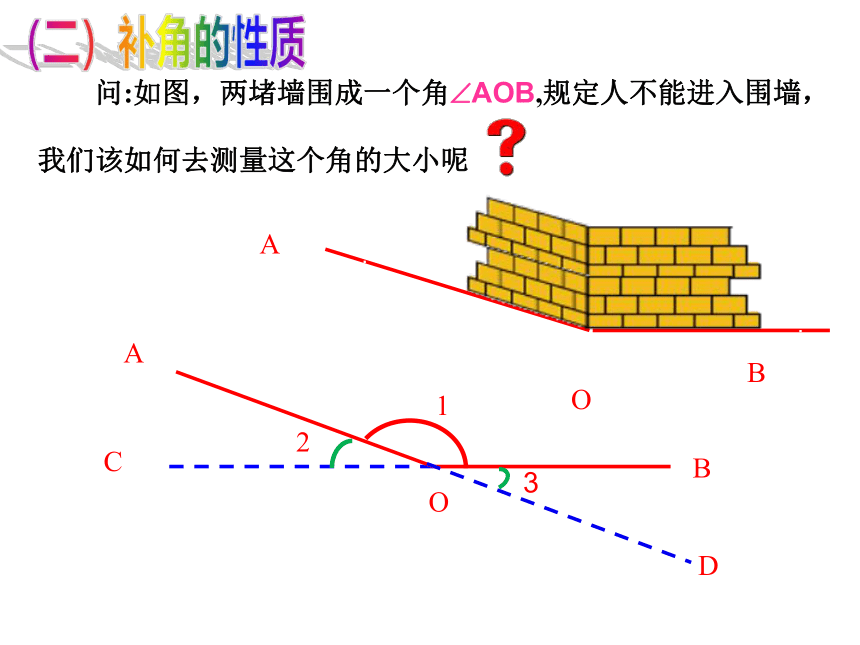
问:如图,两堵墙围成一个角 AOB,规定人不能进入围墙,
我们该如何去测量这个角的大小呢
3
D
如图∠1 与∠2互补,∠1 与∠3互补 ,那么∠2与∠3相等吗?
为什么?
∵ ∠1 +∠2=________,
∴ ∠2= 180 °-___;
∠1
答:∠2=∠3。
∵ ∠1+∠3=_______ ,
∴___________。
∠3 = 180° -∠1
∴________
∠2=∠3
理由如下:
180 °
180 °
1
2
3
探究一
已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,
那么∠2和∠4 相等吗?为什么?
∵ ∠1+∠2=____,
∴ ___________________
∵ ∠3+∠4=_______,
∴ ∠4= ____________________
又∵ ∠1=∠3,
∴ ∠2=∠4.
1
2
3
4
180 -____=180 -_____,
180 -∠1.
180 -∠3.
∠ 1
∠3
探究二
∠2=
180
180
答:∠2=∠4。
理由如下:
几何语言:
∵ ∠1+ ∠ 2 = 1800
∠ 1+ ∠ 3 = 1800
∴ ∠ 2 = ∠ 3
(同角的补角相等)
几何语言:
∵ ∠1 + ∠ 2 = 1800
∠ 3 + ∠ 4 = 1800
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的补角相等)
1.若∠1与∠2互余,∠2与∠3互余,则_____=______,根据是_________.
2.若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是________.
同角的余角相等
等角的补角相等
∠1
∠3
∠4
∠5
四用
3. 如图,O是直线AB上一点,
∠BOC= ∠DOE=90°,请说明:
(1) ∠1= ∠2 ;
(2) ∠COF= ∠AOE .
A
F
D
C
E
B
1
2
O
(1)解:∵ ∠BOC= 90°
即____+____=90°
又∵ ∠DOE= 90°
即____+____ =90°
∴ ∠1= ∠2
3
∠2
∠3
∠1
∠3
(2) 解:∵∠COF+_____= 180°
∠AOE+_____ = 180°
又∵ ∠1= ∠2
∴∠COF= ∠AOE
∠1
∠2
( )
( )
同角的余角相等
等角的补角相等
余角的性质:
补角的性质:
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6
华东师大版数学七年级上册
复习旧知
如果两个角的和等于90°(直角),那么就说这两个角互为余角,简称互余。
如图∠AOD = 90°
∠1+∠2 = 90°
0
A
D
1
2
1
2
∵ ∠1+ ∠2= 90°
∴ ∠1、 ∠2互为余角
∴∠1+∠2=900
∵∠1与∠2互余
利用三角尺画出∠1的余角
1
2
3
已知:∠2与∠3都是∠1的余角。
问: ∠2与∠3的大小关系。
解:∠2=∠3
A
O
B
C
D
探究一
∴ 90°-∠1 =90°- ∠1
即:________。
∵ ∠1 +∠2=90°,
∴ ∠2= 90 °-____;
∵ ∠1 +∠3=90°,
∴ ∠3= 90 °-_____;
∠1
∠1
∠2 =∠3
理由如下:
∵ ∠1 =∠3,
∴ 90°-∠1 =90°- ∠3
即:________。
∵ ∠1 +∠2=90°,
∴ ∠2= 90 °-____;
如图∠1 与∠2互余,∠3与∠4互余 ,如果
∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
3
4
答:∠2=∠4,
∠1
∠2 =∠4
理由如下:
∵ ∠3 +∠4=90°,
∴ ∠4= 90 °-_____;
∠3
探究二
几何语言:
∵ ∠1+ ∠ 2 = 900
∠ 1+ ∠ 3 = 900
∴ ∠ 2 = ∠ 3
(同角的余角相等)
几何语言:
∵ ∠1 + ∠ 2 = 900
∠ 3 + ∠ 4 = 900
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的余角相等)
如果两个角的和等于180°(平角),那么就说
这两个角互为补角,简称互补。
符号语言表示为:
2
1
2
1
复习旧知
∵ ∠1+ ∠2= 180°
∴ ∠1、 ∠2互为补角
∴∠1+∠2=1800
∵∠1与∠2互补
B
A
O
C
O
A
B
1
2
问:如图,两堵墙围成一个角 AOB,规定人不能进入围墙,
我们该如何去测量这个角的大小呢
3
D
如图∠1 与∠2互补,∠1 与∠3互补 ,那么∠2与∠3相等吗?
为什么?
∵ ∠1 +∠2=________,
∴ ∠2= 180 °-___;
∠1
答:∠2=∠3。
∵ ∠1+∠3=_______ ,
∴___________。
∠3 = 180° -∠1
∴________
∠2=∠3
理由如下:
180 °
180 °
1
2
3
探究一
已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,
那么∠2和∠4 相等吗?为什么?
∵ ∠1+∠2=____,
∴ ___________________
∵ ∠3+∠4=_______,
∴ ∠4= ____________________
又∵ ∠1=∠3,
∴ ∠2=∠4.
1
2
3
4
180 -____=180 -_____,
180 -∠1.
180 -∠3.
∠ 1
∠3
探究二
∠2=
180
180
答:∠2=∠4。
理由如下:
几何语言:
∵ ∠1+ ∠ 2 = 1800
∠ 1+ ∠ 3 = 1800
∴ ∠ 2 = ∠ 3
(同角的补角相等)
几何语言:
∵ ∠1 + ∠ 2 = 1800
∠ 3 + ∠ 4 = 1800
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的补角相等)
1.若∠1与∠2互余,∠2与∠3互余,则_____=______,根据是_________.
2.若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是________.
同角的余角相等
等角的补角相等
∠1
∠3
∠4
∠5
四用
3. 如图,O是直线AB上一点,
∠BOC= ∠DOE=90°,请说明:
(1) ∠1= ∠2 ;
(2) ∠COF= ∠AOE .
A
F
D
C
E
B
1
2
O
(1)解:∵ ∠BOC= 90°
即____+____=90°
又∵ ∠DOE= 90°
即____+____ =90°
∴ ∠1= ∠2
3
∠2
∠3
∠1
∠3
(2) 解:∵∠COF+_____= 180°
∠AOE+_____ = 180°
又∵ ∠1= ∠2
∴∠COF= ∠AOE
∠1
∠2
( )
( )
同角的余角相等
等角的补角相等
余角的性质:
补角的性质:
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
