黄金分割竞赛课件

(共24张PPT)
学习目标：
1.理解黄金分割的意义和黄金分割比
2.掌握线段黄金分割点的作法
3.会进行黄金分割的有关计算
摄影作品之美
活动一:探索身边奥妙
A
C
B
度量点C到点A、B的距离,并计算：
AC
BC
AB
AC
=
发现：
黄金分割的定义:
A
C
B
A
C
B
利用一元二次方程可以解出x= ≈
x2 + x–1=0
0.618
1–x
AC
AB
AC
BC
=
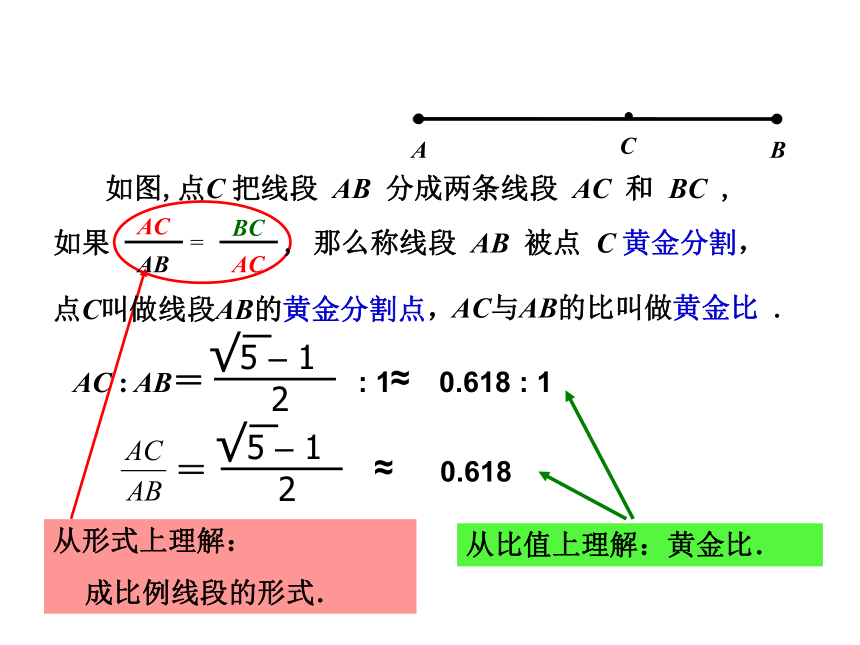
如果 , 那么称线段 AB 被点 C 黄金分割，
点C叫做线段AB的黄金分割点，
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
C
A
B
设 AB=1，AC = x，则 BC= ，
由 列方程得： ，
化为整式方程： ，
1 – x
=
x
x
1
√5 – 1
2
≈
AC : AB＝ : 1 0.618 : 1
从形式上理解：
成比例线段的形式．
√5 – 1
2
≈
＝ 0.618
从比值上理解：黄金比．
AC
AB
AC
BC
=
如果 , 那么称线段 AB 被点 C 黄金分割，
点C叫做线段AB的黄金分割点，
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
C
A
B
B
A
C
面部的黄金分割
寻找我们身边的黄金分割
判断1：如图，线段AB上有一个点C，如果 ，
那么点C是线段AB的黄金分割点吗？
C
A
B
解：根据定义，如果 = ，那么点C叫作线段AB的
黄金分割点，
∵ ， ∴ ，
∴ 点C是线段AB的黄金分割点．
=
2.如图，已知线段AB=1.点C是AB的黄金分割点，AC=__, BC=_____ .
C
A
B
主持人在舞台上主持节目时，站在-------是最佳位置。
如图，线段AB表示舞台，主持人现在的位置是B点，要使他主持节目的位置最佳，又让他走的距离尽可能少，点C在什么位置？
B
A
1．已知线段AB，如何作出它的黄金分割点？
按照如下方法作图：
(１)经过点B作BD⊥AB,使BD= AB.
(２)连接AD，在AD上截取DE=DB.
(３)在AB上截取AC=AE
2．计算
思考：
1．如果设AB=2,那么BD,AD,AC,BC分别等于多少
BD=
AD=
AC=
BC=
3．点C是线段AB的黄金分割点吗
是
如果用图中的虚线表示的矩形画成如图所示的矩形ABCD，以矩形ABCD的宽为边在其内部作正方形AEFD，
那么我们可以惊奇的发现， 。
想一想：点E是AB的黄金分割点吗？
矩形ABCD的宽与长的比是黄金比吗？
BC
BE
BC
AB
=
巴台农神庙
（Parthenom Temple）
A
B
C
D
E
F
BC
BE
BC
AB
=
1.点E是AB的黄金分割点吗？
2.矩形ABCD的宽与长的比是
黄金比吗？
BC
AB
BC
BE
=
AE
AB
AE
BE
=
点E是AB的黄金分割点
AE
AB
（即 ）是黄金比
BC
AB
矩形ABCD的宽与长的比是黄金比
宽与长的比等于黄金比的矩形也称为黄金矩形
A
B
C
D
E
F
如图，点C是线段AB的黄金分割点，AC>BC，
如果AB=4，求线段AC的长度．
C
A
B
=
解：根据定义，如果点C是线段AB的黄金分割点，
那么 = ，
∵点C是线段AB的黄金分割点， ∴ ，
∴ AC= AB = .
×4 = ２( )
A
C
B
A
C
B
A
C
B
在礼品包装中，也经常用到黄金分割．
巴黎圣母院
联合国总部大厦
古希腊巴台农神庙
黄金分割，尤其宽与长的比为黄金比的矩形，在古典及现代建筑中都有广泛的应用．
课本4.2 1、3题