12.2 一次函数(8) 课件(共27张PPT)
文档属性
| 名称 | 12.2 一次函数(8) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 959.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 12:53:31 | ||
图片预览







文档简介
(共27张PPT)
沪科版 八年级上册
12.2 一次函数 (8)
教学目标
1.用一次函数解决实际问题.
2.通过对实际问题的分析、解答,培养学生分析问题、
解决问题的能力.渗透数形结合数学思想方法.
教学重难点
用一次函数解决实际问题.
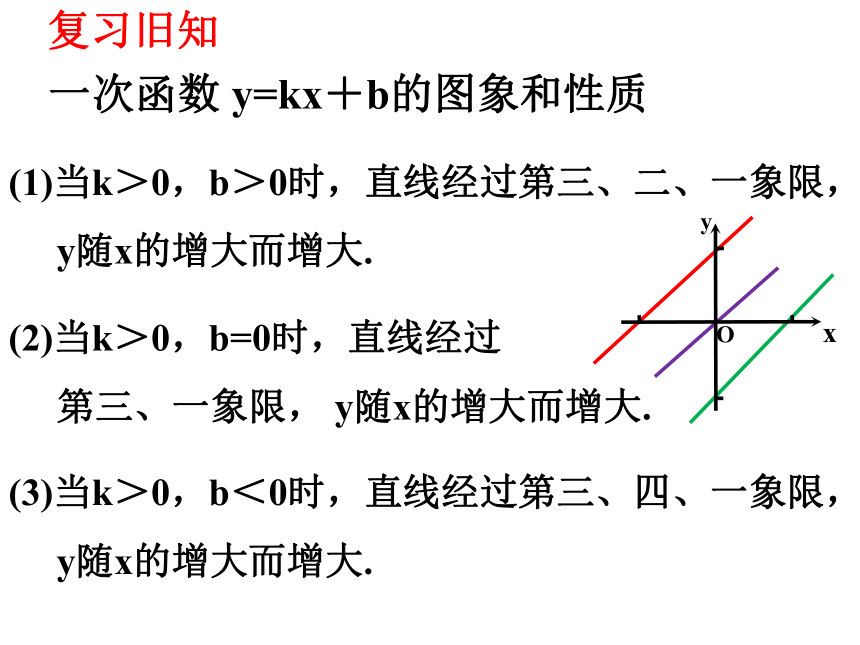
(1)当k>0,b>0时,直线经过第三、二、一象限,
y随x的增大而增大.
一次函数 y=kx+b的图象和性质
(3)当k>0,b<0时,直线经过第三、四、一象限,
y随x的增大而增大.
(2)当k>0,b=0时,直线经过
第三、一象限, y随x的增大而增大.
x
y
O
复习旧知
(4)当k<0,b>0时,直线经过第二、一、四象限,
y随x的增大而减小.
一次函数 y=kx+b的图象和性质
(6)当k<0,b<0时,直线经过第二、三、四象
限,y随x的增大而减小.
(5)当k<0,b=0时,直线经过第二、四象限,
y随x的增大而减小.
x
y
O
温故知新
某作家新出版的科幻小说定价为30元/本,如果一次购买20本以上的,超过20本的部分的价格打8折.
(1)设购买科幻小说的数量为x本,付款金额为y元,则
y关于x 的函数解析式为 .
(2)当购买100本时,应付款 元.
y=30x
y=24x+120
(x>20)
(0≤x≤20)
2520
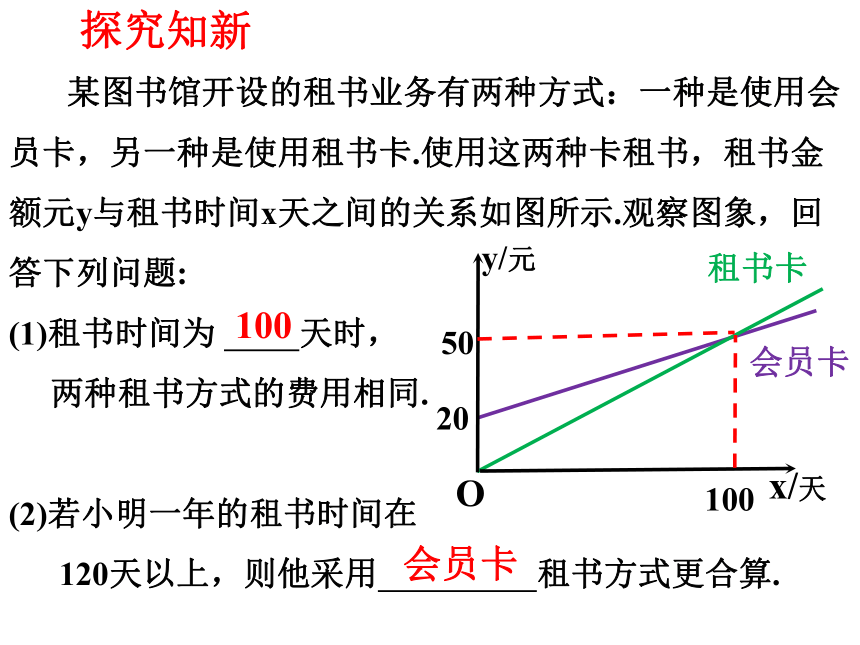
某图书馆开设的租书业务有两种方式:一种是使用会员卡,另一种是使用租书卡.使用这两种卡租书,租书金额元y与租书时间x天之间的关系如图所示.观察图象,回答下列问题:
(1)租书时间为 天时,
两种租书方式的费用相同.
(2)若小明一年的租书时间在
120天以上,则他采用 租书方式更合算.
x/天
y/元
O
租书卡
会员卡
20
50
100
探究知新
100
会员卡
例6 某单位有职工几十人,想在节假日组织到外地H处旅游,当地有甲,乙两家旅行社,他们服务质量基本相同,到H处旅游价格都是每人100元.经联系协商,甲旅行社给每位游客八折优惠,乙旅行社表示单位先交1000元后,给每位游客六折优惠.问该单位选择哪家旅行社,使其支付的旅游总费用较少?
典型例析
例6 某单位有职工几十人,想在节假日组织到外地H处旅游,当地有甲,乙两家旅行社,他们服务质量基本相同,到H处旅游价格都是每人100元.经联系协商,甲旅行社给每位游客八折优惠,乙旅行社表示单位先交1000元后,给每位游客六折优惠.问该单位选择哪家旅行社,使其支付的旅游总费用较少?
解:
设该单位参加旅游的人数为x,
那么如选甲旅行社,
总费用为
如选乙旅行社,
总费用为
80x元,
(60x+1000)元.
解:
设该单位参加旅游的人数为x,
那么如选甲旅行社,
总费用为
如选乙旅行社,
总费用为
80x元,
(60x+1000)元.
记y1=80x,
y2=60x+1000.
在同一直角
坐标系中作出这两个函数的图象.
记y1=80x,
y2=60x+1000.
在同一直角
坐标系中作出这两个函数的图象.
y1
y2
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
x
y
O
观察这两个函数的图象.
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
y1
y2
当人数为50时,
选甲或乙旅行社,
总费用一样.
x
y
O
观察这两个函数的图象.
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
y1
y2
当人数为0~49时,
选甲旅行社,
总费用较少.
x
y
O
观察这两个函数的图象.
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
y1
y2
当人数为51~100时,
选乙旅行社,
总费用较少.
x
y
O
解:
设选择甲、乙旅行社所需费用的差为y,
则y=
y2
y1-
=80x
-(60x+1000)
=20x-1000.
y
O
x
20
40
60
-1000
-600
-200
y=20x-1000
当x=50时,
y=0.
即y1=y2,
选甲或乙旅行社,
总费用一样.
此时
解:
设选择甲、乙旅行社所需费用的差为y,
则y=
y2
y1-
=80x
-(60x+1000)
=20x-1000.
y
O
x
20
40
60
-1000
-600
-200
y=20x-1000
当x>50时,
y>0.
即y1 > y2,
选乙旅行社费用少.
解:
设选择甲、乙旅行社所需费用的差为y,
则y=
y2
y1-
=80x
-(60x+1000)
=20x-1000.
y
O
x
20
40
60
-1000
-600
-200
y=20x-1000
当x<50时,
y<0.
即y1 < y2,
选甲旅行社费用少.
1.某厂日产手套总成本y元与手套日产量x副之
间的关系式为y=5x+40000,而手套出厂价
格为每副10元,试问该厂至少日产手套多少
副才能不亏本?
解:
设利润为Q,
则Q=
y
10x-
=10x
-(5x+40000)
=5x-40000.
∵利润=售价-成本,
∵Q≥0,
∴ 5x-40000≥0,
∴ x≥8000.
答:该厂至少日产手套8000副才能不亏本.
练习巩固
2.某单位急需用车,他们准备和甲、乙两个出租车公司签订月租车合
同.设汽车每行驶xkm,甲公司的月租费是y1元,乙公司的月租费
用y2元,y1、y2分别与x之间关系的图象如图,观察图象回答:
(1)每月行驶的路程在什么范围内时,租乙公司的车合算
(2)每月行驶的路程等于多少时,租两家公司车的费用相同
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位
租哪家的车合算
x/km
y/元
o
1000
3000
1000
2000
1500
2000
y1
y2
甲公司
乙公司
当y<1500km时,
租乙公司的车合算.
2.某单位急需用车,他们准备和甲、乙两个出租车公司签订月租车合
同.设汽车每行驶xkm,甲公司的月租费是y1元,乙公司的月租费
用y2元,y1、y2分别与x之间关系的图象如图,观察图象回答:
(1)每月行驶的路程在什么范围内时,租乙公司的车合算
(2)每月行驶的路程等于多少时,租两家公司车的费用相同
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位
租哪家的车合算
x/km
y/元
o
1000
3000
1000
2000
1500
2000
y1
y2
甲公司
乙公司
当y=1500km时,
租车费用相同.
观察图象回答:
(1)每月行驶的路程在什么范围内时,租乙公司的车合算
(2)每月行驶的路程为多少时,租两家公司车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个
单位租哪家的车合算
x/km
y/元
o
1000
3000
1000
2000
1500
2000
y1
y2
乙公司
甲公司
当y=2300km时,
租甲公司的车合算.
课堂小结:
本节课学习了哪些知识?你积累了哪些经验?还有什么疑惑?
巩固提高
某学校为了绿化校园,计划购进A、B两种树苗共21棵.
已知A种树苗每棵90元,乙种树苗每棵70元.设购买A种树苗棵,购买两种树苗所需费用为元.
(1)求y与x 的函数解析式,其中 0≤x≤21.
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案的费用.
巩固提高
某学校为了绿化校园,计划购进A、B两种树苗共21棵.
已知A种树苗每棵90元,乙种树苗每棵70元.设购买A种树苗棵,购买两种树苗所需费用为元.
(1)求y与x 的函数解析式,其中 0≤x≤21.
解:
(1)
y=
90x
+70(21-x)
即y=20 +1470
(0≤x≤21)
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案的费用.
(2)
∵购买B种树苗的数量少于A种树苗的数量,
∴ 21-x<x,
∴ x>10.5,
∵x是整数,
∴11≤x≤21.
∵k=20>0 ,
∴ y随x的增大而增大.
∴ 当x=11时,y取得最小值.
y取得最小值为
20×11+1470
=1690.
答:使费用最省的方案是购买A种树苗11棵,B种树苗10棵,所需费用为1690元.
今天作业
课本P48页第15、16题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
12.2 一次函数 (8)
教学目标
1.用一次函数解决实际问题.
2.通过对实际问题的分析、解答,培养学生分析问题、
解决问题的能力.渗透数形结合数学思想方法.
教学重难点
用一次函数解决实际问题.
(1)当k>0,b>0时,直线经过第三、二、一象限,
y随x的增大而增大.
一次函数 y=kx+b的图象和性质
(3)当k>0,b<0时,直线经过第三、四、一象限,
y随x的增大而增大.
(2)当k>0,b=0时,直线经过
第三、一象限, y随x的增大而增大.
x
y
O
复习旧知
(4)当k<0,b>0时,直线经过第二、一、四象限,
y随x的增大而减小.
一次函数 y=kx+b的图象和性质
(6)当k<0,b<0时,直线经过第二、三、四象
限,y随x的增大而减小.
(5)当k<0,b=0时,直线经过第二、四象限,
y随x的增大而减小.
x
y
O
温故知新
某作家新出版的科幻小说定价为30元/本,如果一次购买20本以上的,超过20本的部分的价格打8折.
(1)设购买科幻小说的数量为x本,付款金额为y元,则
y关于x 的函数解析式为 .
(2)当购买100本时,应付款 元.
y=30x
y=24x+120
(x>20)
(0≤x≤20)
2520
某图书馆开设的租书业务有两种方式:一种是使用会员卡,另一种是使用租书卡.使用这两种卡租书,租书金额元y与租书时间x天之间的关系如图所示.观察图象,回答下列问题:
(1)租书时间为 天时,
两种租书方式的费用相同.
(2)若小明一年的租书时间在
120天以上,则他采用 租书方式更合算.
x/天
y/元
O
租书卡
会员卡
20
50
100
探究知新
100
会员卡
例6 某单位有职工几十人,想在节假日组织到外地H处旅游,当地有甲,乙两家旅行社,他们服务质量基本相同,到H处旅游价格都是每人100元.经联系协商,甲旅行社给每位游客八折优惠,乙旅行社表示单位先交1000元后,给每位游客六折优惠.问该单位选择哪家旅行社,使其支付的旅游总费用较少?
典型例析
例6 某单位有职工几十人,想在节假日组织到外地H处旅游,当地有甲,乙两家旅行社,他们服务质量基本相同,到H处旅游价格都是每人100元.经联系协商,甲旅行社给每位游客八折优惠,乙旅行社表示单位先交1000元后,给每位游客六折优惠.问该单位选择哪家旅行社,使其支付的旅游总费用较少?
解:
设该单位参加旅游的人数为x,
那么如选甲旅行社,
总费用为
如选乙旅行社,
总费用为
80x元,
(60x+1000)元.
解:
设该单位参加旅游的人数为x,
那么如选甲旅行社,
总费用为
如选乙旅行社,
总费用为
80x元,
(60x+1000)元.
记y1=80x,
y2=60x+1000.
在同一直角
坐标系中作出这两个函数的图象.
记y1=80x,
y2=60x+1000.
在同一直角
坐标系中作出这两个函数的图象.
y1
y2
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
x
y
O
观察这两个函数的图象.
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
y1
y2
当人数为50时,
选甲或乙旅行社,
总费用一样.
x
y
O
观察这两个函数的图象.
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
y1
y2
当人数为0~49时,
选甲旅行社,
总费用较少.
x
y
O
观察这两个函数的图象.
20
40
60
80
100
800
1600
2400
3200
4000
4800
5600
y1
y2
当人数为51~100时,
选乙旅行社,
总费用较少.
x
y
O
解:
设选择甲、乙旅行社所需费用的差为y,
则y=
y2
y1-
=80x
-(60x+1000)
=20x-1000.
y
O
x
20
40
60
-1000
-600
-200
y=20x-1000
当x=50时,
y=0.
即y1=y2,
选甲或乙旅行社,
总费用一样.
此时
解:
设选择甲、乙旅行社所需费用的差为y,
则y=
y2
y1-
=80x
-(60x+1000)
=20x-1000.
y
O
x
20
40
60
-1000
-600
-200
y=20x-1000
当x>50时,
y>0.
即y1 > y2,
选乙旅行社费用少.
解:
设选择甲、乙旅行社所需费用的差为y,
则y=
y2
y1-
=80x
-(60x+1000)
=20x-1000.
y
O
x
20
40
60
-1000
-600
-200
y=20x-1000
当x<50时,
y<0.
即y1 < y2,
选甲旅行社费用少.
1.某厂日产手套总成本y元与手套日产量x副之
间的关系式为y=5x+40000,而手套出厂价
格为每副10元,试问该厂至少日产手套多少
副才能不亏本?
解:
设利润为Q,
则Q=
y
10x-
=10x
-(5x+40000)
=5x-40000.
∵利润=售价-成本,
∵Q≥0,
∴ 5x-40000≥0,
∴ x≥8000.
答:该厂至少日产手套8000副才能不亏本.
练习巩固
2.某单位急需用车,他们准备和甲、乙两个出租车公司签订月租车合
同.设汽车每行驶xkm,甲公司的月租费是y1元,乙公司的月租费
用y2元,y1、y2分别与x之间关系的图象如图,观察图象回答:
(1)每月行驶的路程在什么范围内时,租乙公司的车合算
(2)每月行驶的路程等于多少时,租两家公司车的费用相同
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位
租哪家的车合算
x/km
y/元
o
1000
3000
1000
2000
1500
2000
y1
y2
甲公司
乙公司
当y<1500km时,
租乙公司的车合算.
2.某单位急需用车,他们准备和甲、乙两个出租车公司签订月租车合
同.设汽车每行驶xkm,甲公司的月租费是y1元,乙公司的月租费
用y2元,y1、y2分别与x之间关系的图象如图,观察图象回答:
(1)每月行驶的路程在什么范围内时,租乙公司的车合算
(2)每月行驶的路程等于多少时,租两家公司车的费用相同
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位
租哪家的车合算
x/km
y/元
o
1000
3000
1000
2000
1500
2000
y1
y2
甲公司
乙公司
当y=1500km时,
租车费用相同.
观察图象回答:
(1)每月行驶的路程在什么范围内时,租乙公司的车合算
(2)每月行驶的路程为多少时,租两家公司车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个
单位租哪家的车合算
x/km
y/元
o
1000
3000
1000
2000
1500
2000
y1
y2
乙公司
甲公司
当y=2300km时,
租甲公司的车合算.
课堂小结:
本节课学习了哪些知识?你积累了哪些经验?还有什么疑惑?
巩固提高
某学校为了绿化校园,计划购进A、B两种树苗共21棵.
已知A种树苗每棵90元,乙种树苗每棵70元.设购买A种树苗棵,购买两种树苗所需费用为元.
(1)求y与x 的函数解析式,其中 0≤x≤21.
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案的费用.
巩固提高
某学校为了绿化校园,计划购进A、B两种树苗共21棵.
已知A种树苗每棵90元,乙种树苗每棵70元.设购买A种树苗棵,购买两种树苗所需费用为元.
(1)求y与x 的函数解析式,其中 0≤x≤21.
解:
(1)
y=
90x
+70(21-x)
即y=20 +1470
(0≤x≤21)
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案的费用.
(2)
∵购买B种树苗的数量少于A种树苗的数量,
∴ 21-x<x,
∴ x>10.5,
∵x是整数,
∴11≤x≤21.
∵k=20>0 ,
∴ y随x的增大而增大.
∴ 当x=11时,y取得最小值.
y取得最小值为
20×11+1470
=1690.
答:使费用最省的方案是购买A种树苗11棵,B种树苗10棵,所需费用为1690元.
今天作业
课本P48页第15、16题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
