12.2一次函数(10) 课件(共32张PPT)
文档属性
| 名称 | 12.2一次函数(10) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 963.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 12:15:43 | ||
图片预览







文档简介
(共32张PPT)
沪科版 八年级上册
12.2 一次函数 (10)
教学目标
理解一次函数与一元一次不等式之间的关系,熟练利用一次函数的图象解相应的一元一次不等式.
教学重难点
重点:一次函数与一元一次不等式之间的关系.
难点:一次函数与一元一次不等式之间的关系.
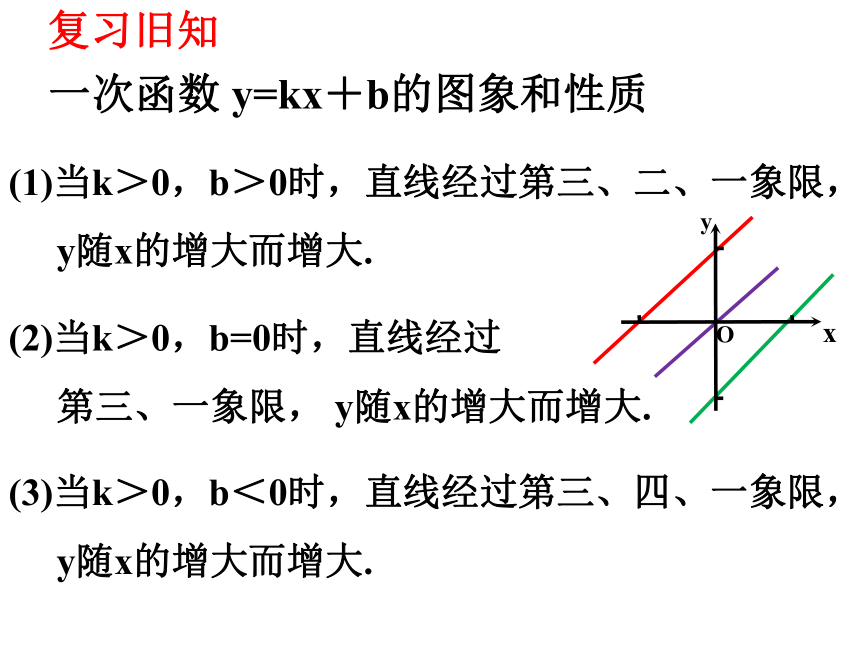
(1)当k>0,b>0时,直线经过第三、二、一象限,
y随x的增大而增大.
一次函数 y=kx+b的图象和性质
(3)当k>0,b<0时,直线经过第三、四、一象限,
y随x的增大而增大.
(2)当k>0,b=0时,直线经过
第三、一象限, y随x的增大而增大.
x
y
O
复习旧知
(4)当k<0,b>0时,直线经过第二、一、四象限,
y随x的增大而减小.
一次函数 y=kx+b的图象和性质
(6)当k<0,b<0时,直线经过第二、三、四象
限,y随x的增大而减小.
(5)当k<0,b=0时,直线经过第二、四象限,
y随x的增大而减小.
x
y
O
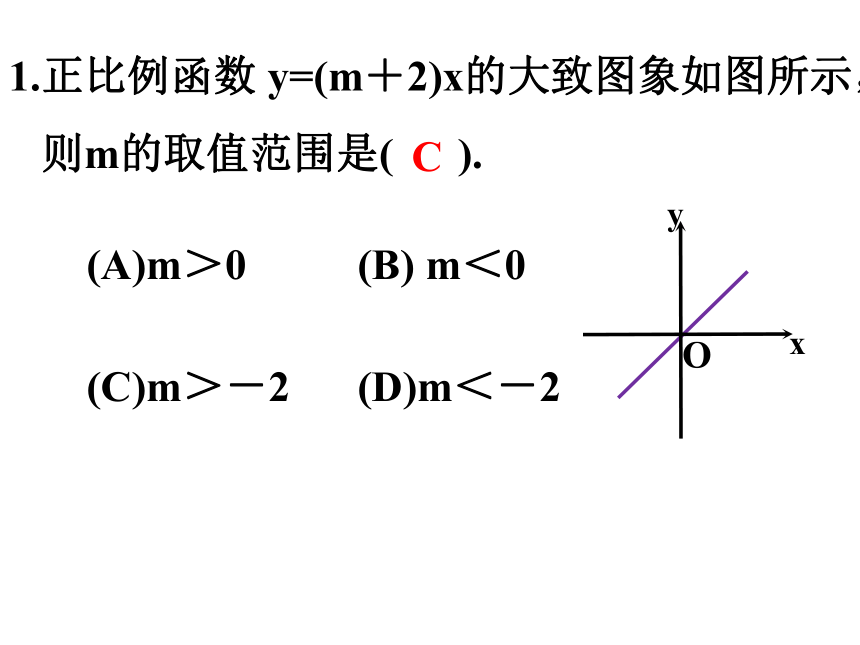
1.正比例函数 y=(m+2)x的大致图象如图所示,
则m的取值范围是( ).
x
y
O
(A)m>0
(B) m<0
(C)m>-2
(D)m<-2
C
2.已知直线y=kx+b,若k+b=-5,kb=6,
则此直线不经过的象限是( ).
(A)第一象限
(B)第二象限
(C)第三象限
(D)第四象限
A
kb=6>0
k>0
b>0
或
k<0
b<0
k+b=-5<0
k<0
b<0
x
y
O
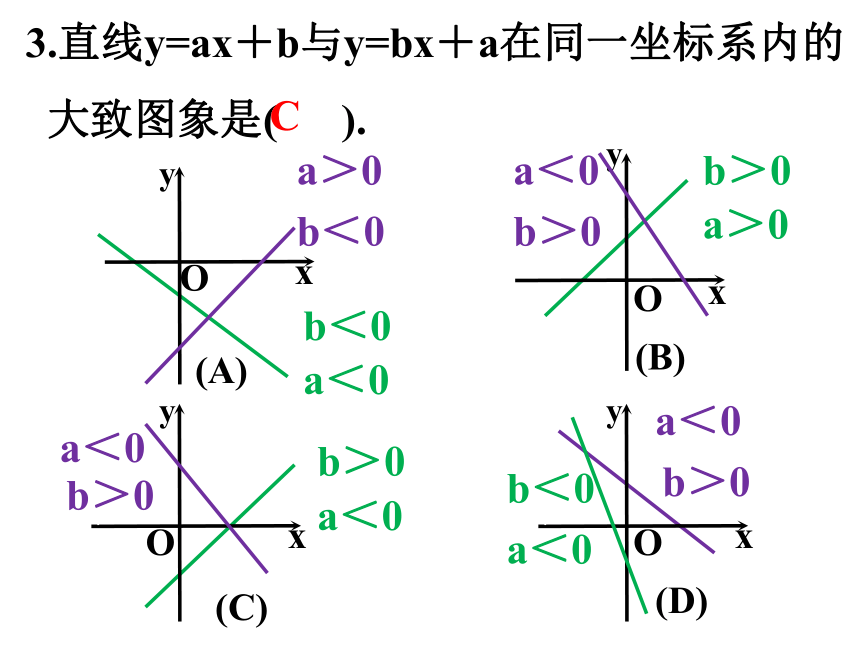
3.直线y=ax+b与y=bx+a在同一坐标系内的
大致图象是( ).
(A)
(B)
(C)
(D)
x
y
O
x
y
O
x
y
O
x
y
O
a>0
b<0
b<0
a<0
a<0
b>0
b>0
a>0
a<0
b>0
b>0
a<0
b>0
a<0
b<0
a<0
C
因为任何一个以x为未知数的一元一次不等式都可以变形为 的形式,
kx+b>0
所以解一元一次不等式kx+b>0或kx+b<0,
都可以转化为求一次函数y=kx+b中y>0时或y<0时的 .
自变量x的取值范围
或kx+b<0
探究新知
根据一次函数 y=2x+6的图象.
x
y
3
O
6
y=2x+6
分别说出不等式2x+6>0和2x+6<0的解集.
2x+6>0,
就是函数 y=2x+6中函数值
y>0.
观察图象:
当图象在x轴的上方时,
图象上的点的纵坐标y
∵ 图象与x 轴的交点坐标为
(-3,0),
∴要使图象在x轴的上方,
x值应在-3的右侧.
即x>-3时,
2x+6>0.
∴不等式2x+6>0的解集为: .
x>-3
>0.
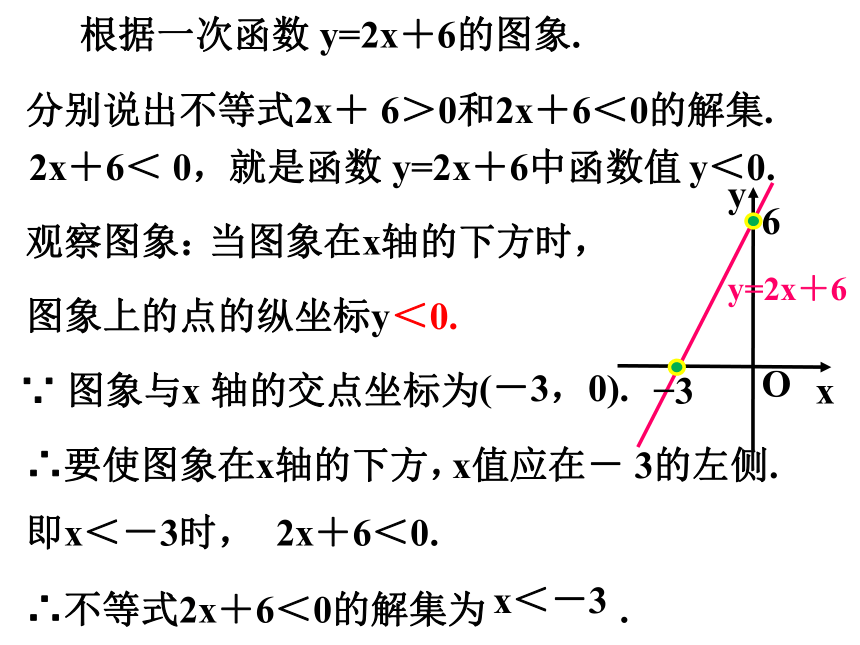
根据一次函数 y=2x+6的图象.
x
y
3
O
6
y=2x+6
分别说出不等式2x+ 6>0和2x+6<0的解集.
2x+6< 0,
就是函数 y=2x+6中函数值
y<0.
观察图象:
当图象在x轴的下方时,
图象上的点的纵坐标y
∵ 图象与x 轴的交点坐标为
(-3,0).
∴要使图象在x轴的下方,
x值应在- 3的左侧.
即x<-3时,
2x+6<0.
∴不等式2x+6<0的解集为 .
x<-3
<0.
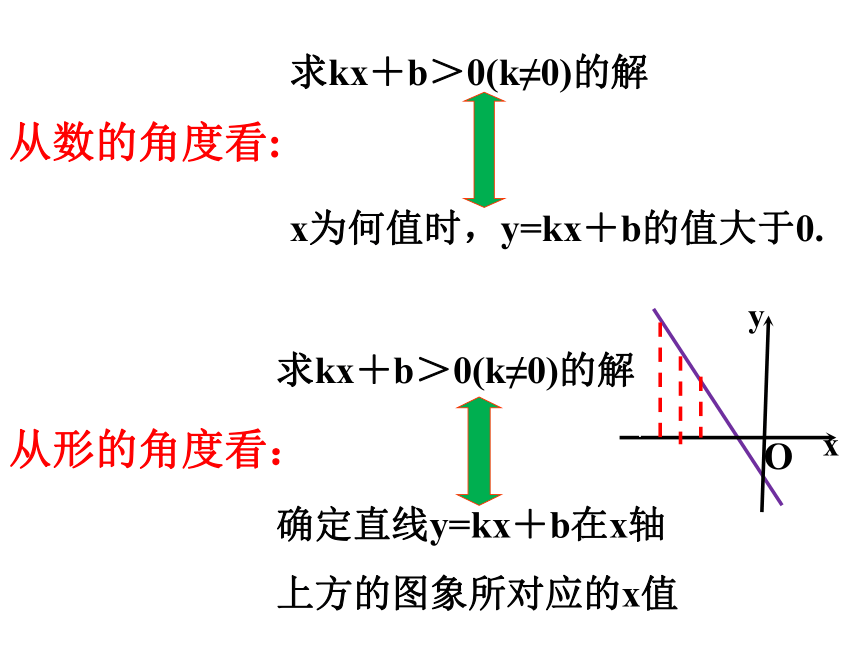
求kx+b>0(k≠0)的解
x为何值时,y=kx+b的值大于0.
确定直线y=kx+b在x轴
上方的图象所对应的x值
从形的角度看:
从数的角度看:
求kx+b>0(k≠0)的解
x
y
O
求kx+b<0(k≠0)的解
x为何值时,y=kx+b的值小于0.
确定直线y=kx+b在x轴
下方的图象所对应的x值.
从形的角度看:
从数的角度看:
求kx+b<0(k≠0)的解
x
y
O
例7.画出函数y=-3x+6的图象,结合图象:
(1)求方程-3x+6=0的解.
(2)求不等式-3x+ 6>0和-3x+6<0的解集.
典型例析
例7.画出函数y=-3x + 6的图象,结合图象:
(1)求方程-3x+6=0的解.
6
x
y
O
2
解:
画函数y=-3x + 6的图象,如图.
图象与x 轴的交点坐标为
(2,0).
∴方程-3x+6=0的解就是图象
与x 轴的交点的横坐标 x 的值:
x=2.
例7.画出函数y=-3x + 6的图象,结合图象:
(2)求不等式-3x+ 6>0和-3x+6<0的解集.
6
x
y
O
2
(2)结合图象可知,
y>0时x的取值范围是
x<2,
y<0时x的取值范围是
x>2.
∴不等式-3x + 6>0的解集为
不等式-3x+6<0的解集为
x<2
x>2.
1.画出一次函数y=-2x-6的图象,结合图象求:
(1)x 时,y=0.
(2)x 时,y > 0.
(3)x 时,y < 0.
(4)x 时,y > 6 .
=-3
<-3
>-3
<-6
y=-2x-6
-6
x
y
O
-3
6
-6
-
练习巩固
2.画出函数y=3x-9的图象,结合图象:
(1)求方程3x-9=0的解.
(2)求不等式3x-9≤0的解集.
(3)当y=3时,求x的值.
(4)当y>3时,求x的取值范围.
2.画出函数y=3x-9的图象,结合图象:
(1)求方程3x-9=0的解.
解:
画函数y=3x- 9的图象,如图.
图象与x 轴的交点坐标为
(3,0).
∴方程3x-9=0的解就是图象
与x 轴的交点的横坐标 x 的值:
x=3.
3
x
y
O
-9
3
2.画出函数y=3x-9的图象,结合图象:
(2)求不等式3x-9≤0的解集.
(2)结合图象可知,
y≤0时x的取值范围是
x≤3,
∴不等式3x - 9≤0的解集为
x≤3.
y=3x-9
3
x
y
O
-9
3
2.画出函数y=3x-9的图象,结合图象:
(3)当y=3时,求x的值.
(4)当y>3时,求x的取值范围.
3
3
x
y
O
-9
4
(3)结合图象可知,
当y=3时,x的值为4.
(4)当y>3时,x的取值范围为
x>4.
例.利用函数图象解不等式:3x-4<x+2
∴不等式的解集为 .
解法1:
化简不等式得
2x-6<0,
画出函数y=2x-6的图象,
当y=2x-6<0时,
y
x
-6
3
O
x<3,
x<3
这表示3x-4<x+2,
例.利用函数图象解不等式:3x-4<x+2
解法2:
画出函数y=3x-4和函数y=x+2的图象,
交点横坐标为3,
当x<3时,对于同一个x,
直线y=3x-4上的点在
直线y=x+2上相应点的下方,
所以不等式的解集为x<3.
y
x
-4
3
O
y=x+2
y=3x-4
2
1. 若函数y=kx+b的图象如图所示,则当y>0时,
x的取值范围是( ).
x
O
y
1
y=kx+b
2
A.x>1 B. x>2 C.x<1 D. x<2
练习巩固
D
2.已知关于x的不等式ax+1>0(a≠0)的解集为x<1.
那么直线y=ax+1与x轴的交点是( ).
A.(0,1) B.(1,0)
C.(0,-1) D.(-1,0)
3.直线y=x-1上的点在x轴上方时对应的自变量的
范围是( ).
A.x>1 B.x≥1 C.x<1 D.x≤1
B
A
课堂小结
1.本节课学习了哪些知识?
2.探究一次函数与一元一次不等式的关系过程中,主要采用了哪些数学方法?
1.已知直线y=2x+k与x轴的交点为(-2,0),则关
于x的不等式2x+k<0的解集是( ).
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
2.对于函数y=-x+4,当x>-2时,y的取
值范围是( ).
A.y<4 B.y>4 C.y>6 D.y<6
巩固提高
C
D
3.如图,直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的解集是( ).
A.x>3 B.-2<x<3
C.x<-2 D.x>-2
x
O
y
A
B
D
4.如图,函数y=2x和y=ax+4的图象相交于点
A(m,3),则不等式2x≥ax+4的解集为( ).
A.x ≥ B.x≥3 C.x ≤ D.x≤3
3
2
3
2
x
O
y
A
A
y=2x
y=ax+4
5.已知直线y=2x-b经过点(2,0),关于x
不等式2x-b≥0的解集是________.
7.直线y=kx+b经过点(3 , 2),(5 , 8)则不等
式组 2≤kx+b<8的解集 .
6.已知直线y=2x-b经过点(1,-1),关于x的
不等式2x-b≥0的解集是________.
x≥2
x≥
3
2
3≤x<5
今天作业
课本P49页第18、19题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
12.2 一次函数 (10)
教学目标
理解一次函数与一元一次不等式之间的关系,熟练利用一次函数的图象解相应的一元一次不等式.
教学重难点
重点:一次函数与一元一次不等式之间的关系.
难点:一次函数与一元一次不等式之间的关系.
(1)当k>0,b>0时,直线经过第三、二、一象限,
y随x的增大而增大.
一次函数 y=kx+b的图象和性质
(3)当k>0,b<0时,直线经过第三、四、一象限,
y随x的增大而增大.
(2)当k>0,b=0时,直线经过
第三、一象限, y随x的增大而增大.
x
y
O
复习旧知
(4)当k<0,b>0时,直线经过第二、一、四象限,
y随x的增大而减小.
一次函数 y=kx+b的图象和性质
(6)当k<0,b<0时,直线经过第二、三、四象
限,y随x的增大而减小.
(5)当k<0,b=0时,直线经过第二、四象限,
y随x的增大而减小.
x
y
O
1.正比例函数 y=(m+2)x的大致图象如图所示,
则m的取值范围是( ).
x
y
O
(A)m>0
(B) m<0
(C)m>-2
(D)m<-2
C
2.已知直线y=kx+b,若k+b=-5,kb=6,
则此直线不经过的象限是( ).
(A)第一象限
(B)第二象限
(C)第三象限
(D)第四象限
A
kb=6>0
k>0
b>0
或
k<0
b<0
k+b=-5<0
k<0
b<0
x
y
O
3.直线y=ax+b与y=bx+a在同一坐标系内的
大致图象是( ).
(A)
(B)
(C)
(D)
x
y
O
x
y
O
x
y
O
x
y
O
a>0
b<0
b<0
a<0
a<0
b>0
b>0
a>0
a<0
b>0
b>0
a<0
b>0
a<0
b<0
a<0
C
因为任何一个以x为未知数的一元一次不等式都可以变形为 的形式,
kx+b>0
所以解一元一次不等式kx+b>0或kx+b<0,
都可以转化为求一次函数y=kx+b中y>0时或y<0时的 .
自变量x的取值范围
或kx+b<0
探究新知
根据一次函数 y=2x+6的图象.
x
y
3
O
6
y=2x+6
分别说出不等式2x+6>0和2x+6<0的解集.
2x+6>0,
就是函数 y=2x+6中函数值
y>0.
观察图象:
当图象在x轴的上方时,
图象上的点的纵坐标y
∵ 图象与x 轴的交点坐标为
(-3,0),
∴要使图象在x轴的上方,
x值应在-3的右侧.
即x>-3时,
2x+6>0.
∴不等式2x+6>0的解集为: .
x>-3
>0.
根据一次函数 y=2x+6的图象.
x
y
3
O
6
y=2x+6
分别说出不等式2x+ 6>0和2x+6<0的解集.
2x+6< 0,
就是函数 y=2x+6中函数值
y<0.
观察图象:
当图象在x轴的下方时,
图象上的点的纵坐标y
∵ 图象与x 轴的交点坐标为
(-3,0).
∴要使图象在x轴的下方,
x值应在- 3的左侧.
即x<-3时,
2x+6<0.
∴不等式2x+6<0的解集为 .
x<-3
<0.
求kx+b>0(k≠0)的解
x为何值时,y=kx+b的值大于0.
确定直线y=kx+b在x轴
上方的图象所对应的x值
从形的角度看:
从数的角度看:
求kx+b>0(k≠0)的解
x
y
O
求kx+b<0(k≠0)的解
x为何值时,y=kx+b的值小于0.
确定直线y=kx+b在x轴
下方的图象所对应的x值.
从形的角度看:
从数的角度看:
求kx+b<0(k≠0)的解
x
y
O
例7.画出函数y=-3x+6的图象,结合图象:
(1)求方程-3x+6=0的解.
(2)求不等式-3x+ 6>0和-3x+6<0的解集.
典型例析
例7.画出函数y=-3x + 6的图象,结合图象:
(1)求方程-3x+6=0的解.
6
x
y
O
2
解:
画函数y=-3x + 6的图象,如图.
图象与x 轴的交点坐标为
(2,0).
∴方程-3x+6=0的解就是图象
与x 轴的交点的横坐标 x 的值:
x=2.
例7.画出函数y=-3x + 6的图象,结合图象:
(2)求不等式-3x+ 6>0和-3x+6<0的解集.
6
x
y
O
2
(2)结合图象可知,
y>0时x的取值范围是
x<2,
y<0时x的取值范围是
x>2.
∴不等式-3x + 6>0的解集为
不等式-3x+6<0的解集为
x<2
x>2.
1.画出一次函数y=-2x-6的图象,结合图象求:
(1)x 时,y=0.
(2)x 时,y > 0.
(3)x 时,y < 0.
(4)x 时,y > 6 .
=-3
<-3
>-3
<-6
y=-2x-6
-6
x
y
O
-3
6
-6
-
练习巩固
2.画出函数y=3x-9的图象,结合图象:
(1)求方程3x-9=0的解.
(2)求不等式3x-9≤0的解集.
(3)当y=3时,求x的值.
(4)当y>3时,求x的取值范围.
2.画出函数y=3x-9的图象,结合图象:
(1)求方程3x-9=0的解.
解:
画函数y=3x- 9的图象,如图.
图象与x 轴的交点坐标为
(3,0).
∴方程3x-9=0的解就是图象
与x 轴的交点的横坐标 x 的值:
x=3.
3
x
y
O
-9
3
2.画出函数y=3x-9的图象,结合图象:
(2)求不等式3x-9≤0的解集.
(2)结合图象可知,
y≤0时x的取值范围是
x≤3,
∴不等式3x - 9≤0的解集为
x≤3.
y=3x-9
3
x
y
O
-9
3
2.画出函数y=3x-9的图象,结合图象:
(3)当y=3时,求x的值.
(4)当y>3时,求x的取值范围.
3
3
x
y
O
-9
4
(3)结合图象可知,
当y=3时,x的值为4.
(4)当y>3时,x的取值范围为
x>4.
例.利用函数图象解不等式:3x-4<x+2
∴不等式的解集为 .
解法1:
化简不等式得
2x-6<0,
画出函数y=2x-6的图象,
当y=2x-6<0时,
y
x
-6
3
O
x<3,
x<3
这表示3x-4<x+2,
例.利用函数图象解不等式:3x-4<x+2
解法2:
画出函数y=3x-4和函数y=x+2的图象,
交点横坐标为3,
当x<3时,对于同一个x,
直线y=3x-4上的点在
直线y=x+2上相应点的下方,
所以不等式的解集为x<3.
y
x
-4
3
O
y=x+2
y=3x-4
2
1. 若函数y=kx+b的图象如图所示,则当y>0时,
x的取值范围是( ).
x
O
y
1
y=kx+b
2
A.x>1 B. x>2 C.x<1 D. x<2
练习巩固
D
2.已知关于x的不等式ax+1>0(a≠0)的解集为x<1.
那么直线y=ax+1与x轴的交点是( ).
A.(0,1) B.(1,0)
C.(0,-1) D.(-1,0)
3.直线y=x-1上的点在x轴上方时对应的自变量的
范围是( ).
A.x>1 B.x≥1 C.x<1 D.x≤1
B
A
课堂小结
1.本节课学习了哪些知识?
2.探究一次函数与一元一次不等式的关系过程中,主要采用了哪些数学方法?
1.已知直线y=2x+k与x轴的交点为(-2,0),则关
于x的不等式2x+k<0的解集是( ).
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
2.对于函数y=-x+4,当x>-2时,y的取
值范围是( ).
A.y<4 B.y>4 C.y>6 D.y<6
巩固提高
C
D
3.如图,直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的解集是( ).
A.x>3 B.-2<x<3
C.x<-2 D.x>-2
x
O
y
A
B
D
4.如图,函数y=2x和y=ax+4的图象相交于点
A(m,3),则不等式2x≥ax+4的解集为( ).
A.x ≥ B.x≥3 C.x ≤ D.x≤3
3
2
3
2
x
O
y
A
A
y=2x
y=ax+4
5.已知直线y=2x-b经过点(2,0),关于x
不等式2x-b≥0的解集是________.
7.直线y=kx+b经过点(3 , 2),(5 , 8)则不等
式组 2≤kx+b<8的解集 .
6.已知直线y=2x-b经过点(1,-1),关于x的
不等式2x-b≥0的解集是________.
x≥2
x≥
3
2
3≤x<5
今天作业
课本P49页第18、19题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
