12.3 一次函数与二元一次方程(1) 课件(共28张PPT)
文档属性
| 名称 | 12.3 一次函数与二元一次方程(1) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 965.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 12:40:07 | ||
图片预览






文档简介
(共28张PPT)
沪科版 八年级上册
12.3 一次函数与二元一次方程 (1)
教学目标
1.初步理解二元一次方程与一次函数的关系.
2.能根据一次函数的图象求二元一次方程的近似解.
3.在学生的思考和操作基础上,了解方程与图象之间的
关系,同时培养了学生的数形结合的意识和能力.
教学重点
1.二元一次方程和一次函数的关系;
2.能根据一次函数的图象求二元一次方程的近似解.
教学难点:方程和函数之间的对应关系即数形结合的
意识和能力.
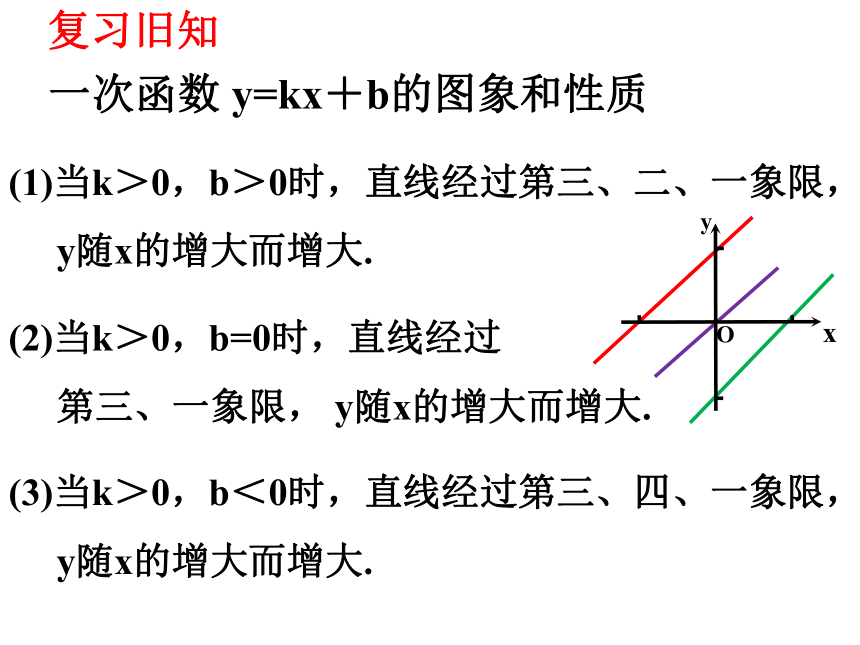
(1)当k>0,b>0时,直线经过第三、二、一象限,
y随x的增大而增大.
一次函数 y=kx+b的图象和性质
(3)当k>0,b<0时,直线经过第三、四、一象限,
y随x的增大而增大.
(2)当k>0,b=0时,直线经过
第三、一象限, y随x的增大而增大.
x
y
O
复习旧知
(4)当k<0,b>0时,直线经过第二、一、四象限,
y随x的增大而减小.
一次函数 y=kx+b的图象和性质
(6)当k<0,b<0时,直线经过第二、三、四象
限,y随x的增大而减小.
(5)当k<0,b=0时,直线经过第二、四象限,
y随x的增大而减小.
x
y
O
1.对于函数y=k2x,(k是常数,k≠0)的图象,
下列说法不正确是( ).
(A)是一条直线
(B)过点( ,k)
(C)经过第二、四象限
(D)y随x的增大而增大
k
1
C
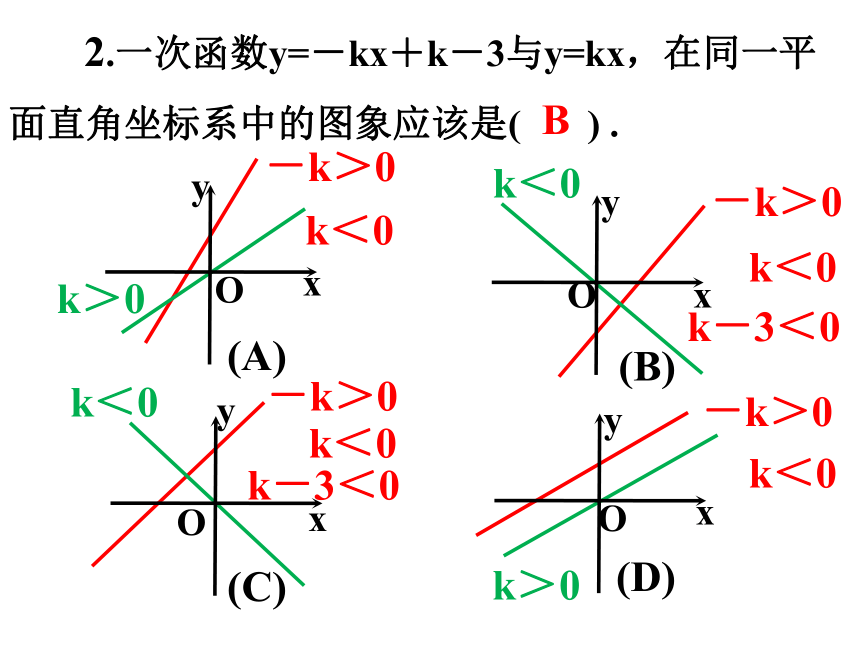
2.一次函数y=-kx+k-3与y=kx,在同一平面直角坐标系中的图象应该是( ) .
x
y
O
(A)
x
y
O
(B)
x
y
O
(C)
x
y
O
(D)
k>0
-k>0
k<0
k<0
-k>0
k<0
k-3<0
k<0
-k>0
k<0
k-3<0
k>0
-k>0
k<0
B
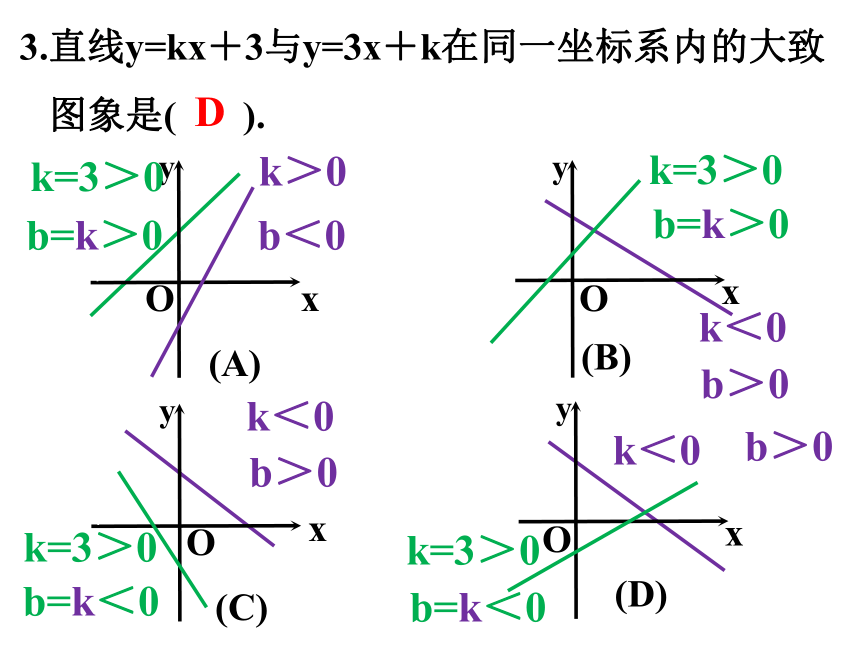
3.直线y=kx+3与y=3x+k在同一坐标系内的大致
图象是( ).
(A)
(B)
(C)
(D)
x
y
O
x
y
O
x
y
O
x
y
O
k>0
b<0
b=k>0
k=3>0
k<0
b>0
k=3>0
b=k>0
k<0
b>0
k=3>0
b=k<0
k<0
b>0
k=3>0
b=k<0
D
求kx+b=0(k≠0)的解
x为何值时,y=kx+b的值为0.
确定直线y=kx+b与x轴的横坐标.
从形的角度看:
从数的角度看:
求kx+b=0(k≠0)的解
知识回顾
1.写出一个二元一次方程.
2.一个二元一次方程有多少组解?
3.一次函数的图象是什么
2x+y=2;
4x-2y=3;
y=2x+2.
将下列二元一次方程转化用x表示y的形式:
① 2x+y=2;
②3x-y=3 ;
③ 4x-2y=3;
④3x+2y=6.
① y=-2x+2;
② y=3x-3 ;
③ y=2x- ;
3
2
④ y=- x+3.
3
2
一个二元一次方程可转化为一次函数的形式.
一次函数的表达式可看成一个二元一次方程.
mx+ny=c
y=kx+b
请写出函数y=- x+3的图象上的任意5个点的坐标,你写出的5个点的坐标是否都满足方程3x+2y=6?你是怎么验证的?
(-4,9)
(-2,6)
(0,3)
(2,0)
(4,-3)
3
2
探究新知
以方程3x+2y=6的所有解组成的坐标是否都在一次函数y=- x+3的图象上?
3
2
二元一次方程3x+2y=6有无数多组解,
以方程3x+2y=6的所有解为坐标,在坐标平面内描点作图,得到一条直线,这条直线就是一次函数y=- x+3的图象.
3
2
方程3x+2y=6的所有解组成的坐标都在一次函数y=- x+3的图象上.
3
2
一般地,一个二元一次方程mx+ny=d可以转化成一次函数y=kx+b(k,b为常数,且k ≠ 0)的形式,所以,每个二元一次方程都对应一个一次函数,也对应一条直线.
二元一次方程的解和一次函数图象上的点的坐标之间是什么关系?
以二元一次方程的解为坐标的点,它都在其相应的一次函数的图象上;一次函数图象上点的坐标,都适合其相应的二元一次方程.
1.已知函数y=6-ax的图象过点(1,2),
则方程 ax+y=6必有一组解是 .
x=1
y=2
练习巩固
2.已知:如图所示,求出直线 L 对应的方程 .
x
2
0
3
y
-1
解:∵L:y=kx+b经过点
∴
-k+b=3
2k+b=0
解这个方程组,得
k=-1
b=2
∴直线L对应的方程为
(-1,3)、
(2,0)
y=-x+2.
1.在平面直角坐标系中画出下列二元一次方程所对应的直线:
(1)x-y=0
(2)x+y=0
(1) y=x
(2) y=-x
x
y
O
1
1
-1
-1
y=x
x
y
O
1
1
-1
-1
y=-x
2.(1)下面的有序数对,哪些是二元一次方程3x+y=6的解?
A(2,0),
B(3,-3),
C(5,-9),
D(6,-10),
E(-2,10),
F(-3,15).
(2)给出二元一次方程3x+y=6任意
五组非整数的解.
(1.5,1.5),
(0.5,4.5),
(-0.5,7.5),
(2.5,-1.5),
(0.1,4.7).
3.有5角、1元的硬币各若干个,从中取出一些凑成4元.问有多少种不同取法?
解:
设取5角的x个,1元的y个,
则有0.5x+y=4,
求它的整数解.
x
y
0
2
4
6
8
4
3
2
1
0
有5种不同取法.
3.有5角、1元的硬币各若干个,从中取出一些凑成4元.问有多少种不同取法?
解:
设取5角的x个,1元的y个,
则有0.5x+y=4,
∴y=4-0.5x
∵x、y都要是非负整数,
∴x必须是2的倍数,
且0.5x≤4.
∴x可取的值只有
0,2,4,6,8,
∴相应的y值为
4,3,3,1,0,
∴有5种不同取法.
即x≤8.
课堂小结
(1)通过本节课的学习,你获得哪些知识?
(2)对本节课的知识探讨过程中,主要运用什么方法?(特殊到一般、数形结合)
巩固提高
1.把二元一次方程x+4y=8化成一次函数的y=kx+b形式,正确的是( ).
A. y= x+8
C. y=- x+2
1
4
B. y= x+2
1
4
1
4
D. y=- x+2
1
4
D
2.下列四条直线中,直线上的点的坐标都是二元一次方程x-2y=2的解的是( ).
x
O
y
-2
2
x
O
y
-2
1
x
O
y
-1
2
x
O
y
-0.5
1
A.
B.
C.
D.
C
3.以二元一次方程y=2x-2的解为坐标的点组成的图象是( ).
x
O
y
1
2
x
O
y
-2
1
x
O
y
-1
2
x
O
y
2
1
A.
B.
C.
D.
B
4.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=- x+b-1的图象上,则常数b的值是( ).
1
2
A.
B.2
C. -1
D.1
1
2
A
今天作业
课本P81页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
12.3 一次函数与二元一次方程 (1)
教学目标
1.初步理解二元一次方程与一次函数的关系.
2.能根据一次函数的图象求二元一次方程的近似解.
3.在学生的思考和操作基础上,了解方程与图象之间的
关系,同时培养了学生的数形结合的意识和能力.
教学重点
1.二元一次方程和一次函数的关系;
2.能根据一次函数的图象求二元一次方程的近似解.
教学难点:方程和函数之间的对应关系即数形结合的
意识和能力.
(1)当k>0,b>0时,直线经过第三、二、一象限,
y随x的增大而增大.
一次函数 y=kx+b的图象和性质
(3)当k>0,b<0时,直线经过第三、四、一象限,
y随x的增大而增大.
(2)当k>0,b=0时,直线经过
第三、一象限, y随x的增大而增大.
x
y
O
复习旧知
(4)当k<0,b>0时,直线经过第二、一、四象限,
y随x的增大而减小.
一次函数 y=kx+b的图象和性质
(6)当k<0,b<0时,直线经过第二、三、四象
限,y随x的增大而减小.
(5)当k<0,b=0时,直线经过第二、四象限,
y随x的增大而减小.
x
y
O
1.对于函数y=k2x,(k是常数,k≠0)的图象,
下列说法不正确是( ).
(A)是一条直线
(B)过点( ,k)
(C)经过第二、四象限
(D)y随x的增大而增大
k
1
C
2.一次函数y=-kx+k-3与y=kx,在同一平面直角坐标系中的图象应该是( ) .
x
y
O
(A)
x
y
O
(B)
x
y
O
(C)
x
y
O
(D)
k>0
-k>0
k<0
k<0
-k>0
k<0
k-3<0
k<0
-k>0
k<0
k-3<0
k>0
-k>0
k<0
B
3.直线y=kx+3与y=3x+k在同一坐标系内的大致
图象是( ).
(A)
(B)
(C)
(D)
x
y
O
x
y
O
x
y
O
x
y
O
k>0
b<0
b=k>0
k=3>0
k<0
b>0
k=3>0
b=k>0
k<0
b>0
k=3>0
b=k<0
k<0
b>0
k=3>0
b=k<0
D
求kx+b=0(k≠0)的解
x为何值时,y=kx+b的值为0.
确定直线y=kx+b与x轴的横坐标.
从形的角度看:
从数的角度看:
求kx+b=0(k≠0)的解
知识回顾
1.写出一个二元一次方程.
2.一个二元一次方程有多少组解?
3.一次函数的图象是什么
2x+y=2;
4x-2y=3;
y=2x+2.
将下列二元一次方程转化用x表示y的形式:
① 2x+y=2;
②3x-y=3 ;
③ 4x-2y=3;
④3x+2y=6.
① y=-2x+2;
② y=3x-3 ;
③ y=2x- ;
3
2
④ y=- x+3.
3
2
一个二元一次方程可转化为一次函数的形式.
一次函数的表达式可看成一个二元一次方程.
mx+ny=c
y=kx+b
请写出函数y=- x+3的图象上的任意5个点的坐标,你写出的5个点的坐标是否都满足方程3x+2y=6?你是怎么验证的?
(-4,9)
(-2,6)
(0,3)
(2,0)
(4,-3)
3
2
探究新知
以方程3x+2y=6的所有解组成的坐标是否都在一次函数y=- x+3的图象上?
3
2
二元一次方程3x+2y=6有无数多组解,
以方程3x+2y=6的所有解为坐标,在坐标平面内描点作图,得到一条直线,这条直线就是一次函数y=- x+3的图象.
3
2
方程3x+2y=6的所有解组成的坐标都在一次函数y=- x+3的图象上.
3
2
一般地,一个二元一次方程mx+ny=d可以转化成一次函数y=kx+b(k,b为常数,且k ≠ 0)的形式,所以,每个二元一次方程都对应一个一次函数,也对应一条直线.
二元一次方程的解和一次函数图象上的点的坐标之间是什么关系?
以二元一次方程的解为坐标的点,它都在其相应的一次函数的图象上;一次函数图象上点的坐标,都适合其相应的二元一次方程.
1.已知函数y=6-ax的图象过点(1,2),
则方程 ax+y=6必有一组解是 .
x=1
y=2
练习巩固
2.已知:如图所示,求出直线 L 对应的方程 .
x
2
0
3
y
-1
解:∵L:y=kx+b经过点
∴
-k+b=3
2k+b=0
解这个方程组,得
k=-1
b=2
∴直线L对应的方程为
(-1,3)、
(2,0)
y=-x+2.
1.在平面直角坐标系中画出下列二元一次方程所对应的直线:
(1)x-y=0
(2)x+y=0
(1) y=x
(2) y=-x
x
y
O
1
1
-1
-1
y=x
x
y
O
1
1
-1
-1
y=-x
2.(1)下面的有序数对,哪些是二元一次方程3x+y=6的解?
A(2,0),
B(3,-3),
C(5,-9),
D(6,-10),
E(-2,10),
F(-3,15).
(2)给出二元一次方程3x+y=6任意
五组非整数的解.
(1.5,1.5),
(0.5,4.5),
(-0.5,7.5),
(2.5,-1.5),
(0.1,4.7).
3.有5角、1元的硬币各若干个,从中取出一些凑成4元.问有多少种不同取法?
解:
设取5角的x个,1元的y个,
则有0.5x+y=4,
求它的整数解.
x
y
0
2
4
6
8
4
3
2
1
0
有5种不同取法.
3.有5角、1元的硬币各若干个,从中取出一些凑成4元.问有多少种不同取法?
解:
设取5角的x个,1元的y个,
则有0.5x+y=4,
∴y=4-0.5x
∵x、y都要是非负整数,
∴x必须是2的倍数,
且0.5x≤4.
∴x可取的值只有
0,2,4,6,8,
∴相应的y值为
4,3,3,1,0,
∴有5种不同取法.
即x≤8.
课堂小结
(1)通过本节课的学习,你获得哪些知识?
(2)对本节课的知识探讨过程中,主要运用什么方法?(特殊到一般、数形结合)
巩固提高
1.把二元一次方程x+4y=8化成一次函数的y=kx+b形式,正确的是( ).
A. y= x+8
C. y=- x+2
1
4
B. y= x+2
1
4
1
4
D. y=- x+2
1
4
D
2.下列四条直线中,直线上的点的坐标都是二元一次方程x-2y=2的解的是( ).
x
O
y
-2
2
x
O
y
-2
1
x
O
y
-1
2
x
O
y
-0.5
1
A.
B.
C.
D.
C
3.以二元一次方程y=2x-2的解为坐标的点组成的图象是( ).
x
O
y
1
2
x
O
y
-2
1
x
O
y
-1
2
x
O
y
2
1
A.
B.
C.
D.
B
4.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=- x+b-1的图象上,则常数b的值是( ).
1
2
A.
B.2
C. -1
D.1
1
2
A
今天作业
课本P81页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
