八年级数学上册《11.2.2三角形的外角》课件(32页PPT)
文档属性
| 名称 | 八年级数学上册《11.2.2三角形的外角》课件(32页PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 12:10:58 | ||
图片预览



文档简介
(共34张PPT)
11.2.2三角形的外角
人教版八年级上册
第十一章 三角形
教学目标
1、在操作活动中,探索并了解三角形的外角的两条性质。
2、利用学过的定理论证这些性质。
3、能利用三角形的外角性质解决与外角有关的实际问题。
新知导入
B
D
C
A
O
●
40 °
70 °
?
●
●
●
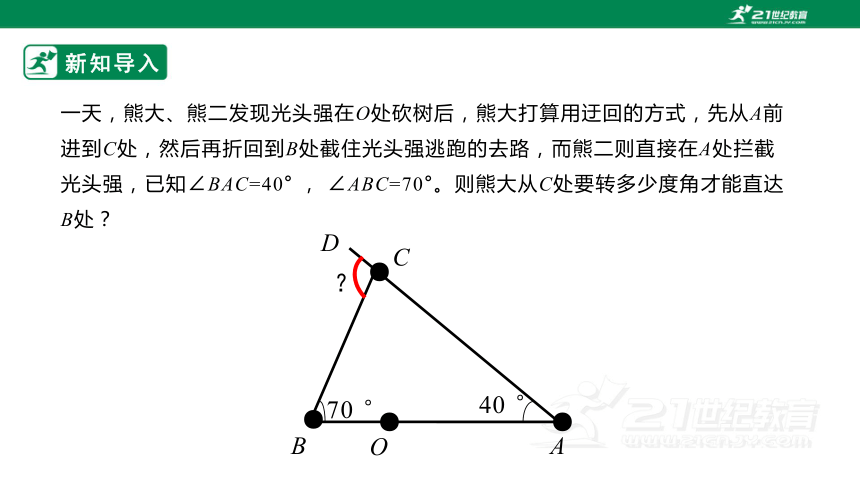
一天,熊大、熊二发现光头强在O处砍树后,熊大打算用迂回的方式,先从A前进到C处,然后再折回到B处截住光头强逃跑的去路,而熊二则直接在A处拦截光头强,已知∠BAC=40° , ∠ABC=70°。则熊大从C处要转多少度角才能直达B处?
新知导入
思路分析:根据三角形内角和定理,可求得∠ACB;
再根据平角为180°可求得∠DCB。
解:由三角形定理可得,∠A+∠B+∠ACB=180°
∴∠ACB=180°-∠A-∠B
=180°-40°-70°
=70°
∵∠ACB+∠DCB=180°
∴∠DCB=180°-∠ACB
=180°-70°
=110°
∠DCB=110°,而∠A+∠B=110°,像∠DCB这样
的角有什么特征吗?它又具有什么性质呢?
是不是这样的角都具有上述的等量关系呢?
新知讲解
一、三角形的外角
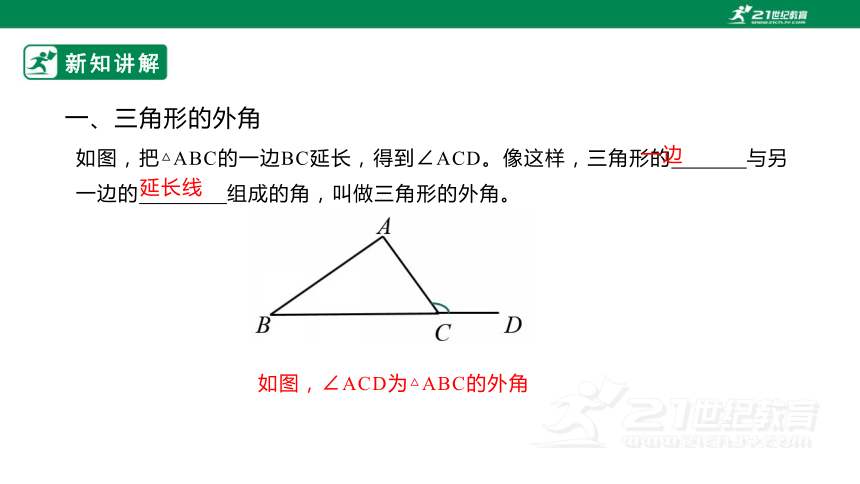
如图,把△ABC的一边BC延长,得到∠ACD。像这样,三角形的 与另
一边的 组成的角,叫做三角形的外角。
延长线
一边
如图,∠ACD为△ABC的外角
新知讲解
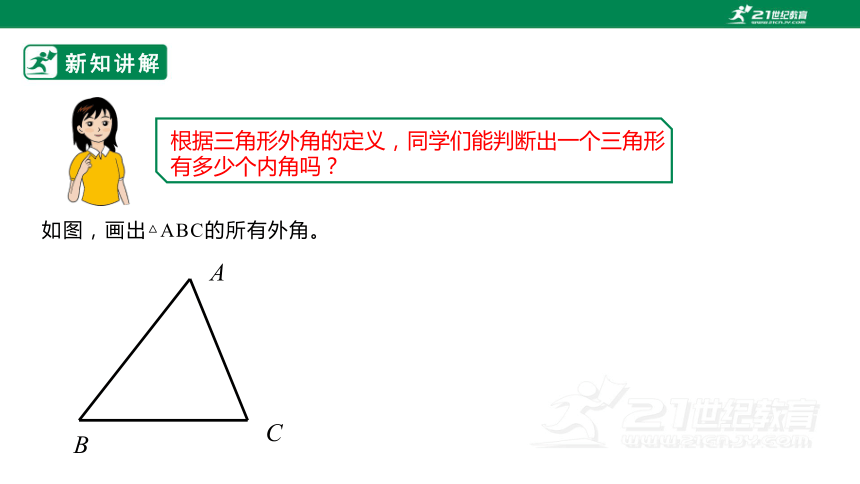
根据三角形外角的定义,同学们能判断出一个三角形有多少个内角吗?
如图,画出△ABC的所有外角。
A
B
C
新知讲解
A
B
C
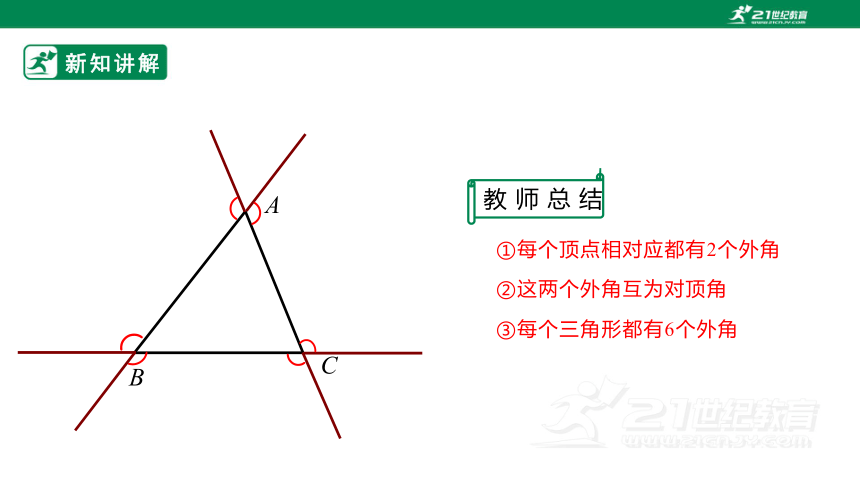
教 师 总 结
①每个顶点相对应都有2个外角
②这两个外角互为对顶角
③每个三角形都有6个外角
新知讲解
二、三角形的外角的性质
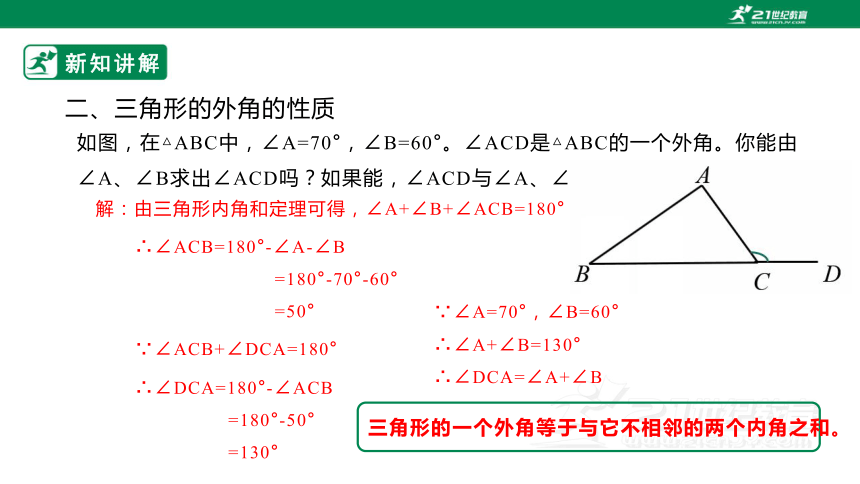
如图,在△ABC中,∠A=70°,∠B=60°。∠ACD是△ABC的一个外角。你能由∠A、∠B求出∠ACD吗?如果能,∠ACD与∠A、∠B有什么关系?
解:由三角形内角和定理可得,∠A+∠B+∠ACB=180°
∴∠ACB=180°-∠A-∠B
=180°-70°-60°
=50°
∵∠ACB+∠DCA=180°
∴∠DCA=180°-∠ACB
=180°-50°
=130°
∵∠A=70°,∠B=60°
∴∠A+∠B=130°
∴∠DCA=∠A+∠B
三角形的一个外角等于与它不相邻的两个内角之和。
新知讲解
验 证 结 论
A
B
D
C
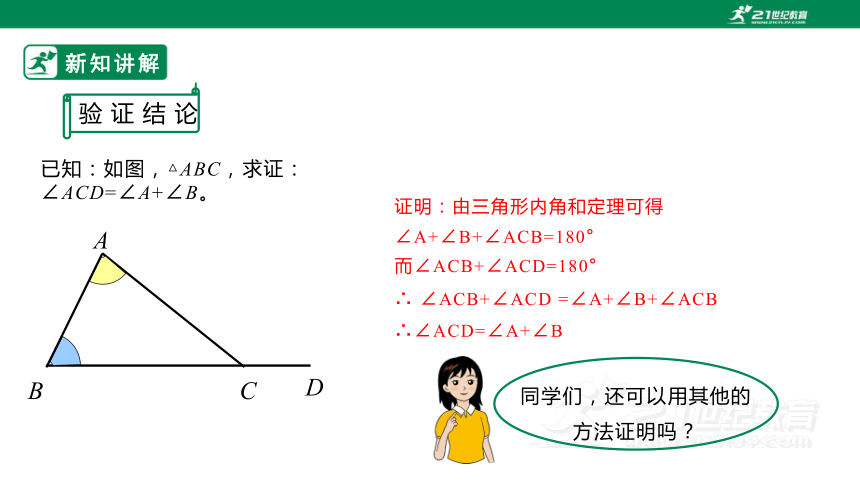
已知:如图,△ABC,求证:∠ACD=∠A+∠B。
证明:由三角形内角和定理可得
∠A+∠B+∠ACB=180°
而∠ACB+∠ACD=180°
∴ ∠ACB+∠ACD =∠A+∠B+∠ACB
∴∠ACD=∠A+∠B
同学们,还可以用其他的
方法证明吗?
新知讲解
1
2
A
B
D
C
E
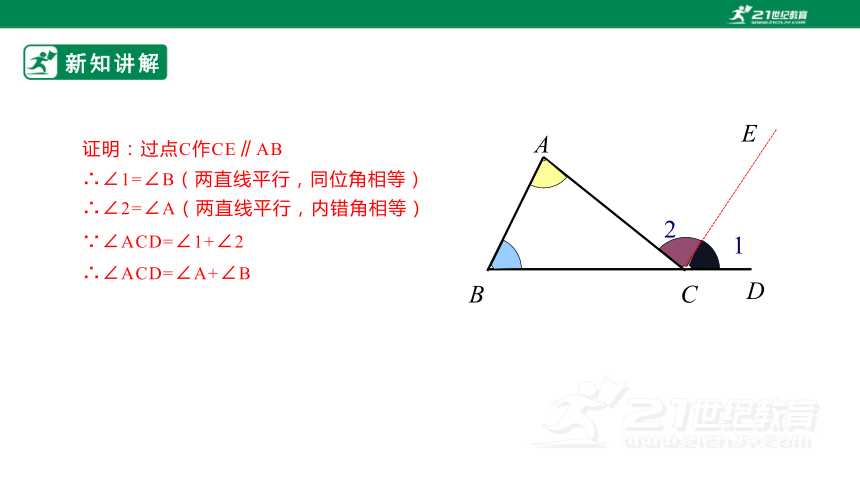
证明:过点C作CE∥AB
∴∠1=∠B(两直线平行,同位角相等)
∴∠2=∠A(两直线平行,内错角相等)
∵∠ACD=∠1+∠2
∴∠ACD=∠A+∠B
新知讲解
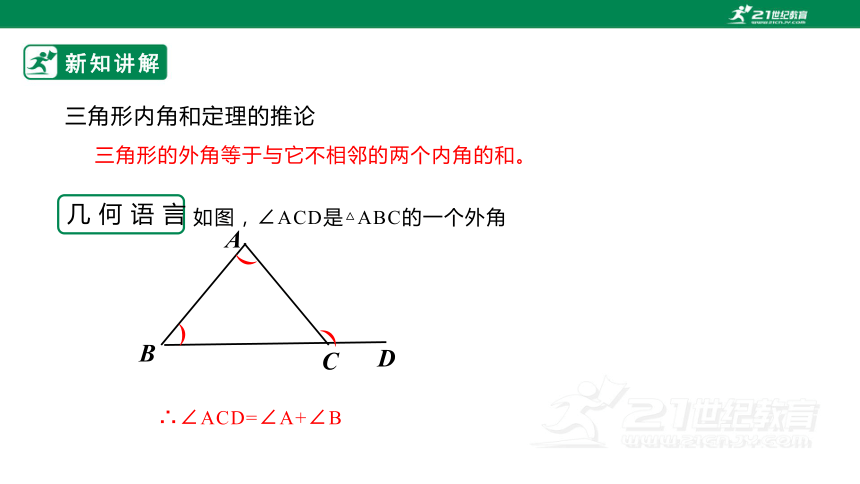
三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和。
几 何 语 言
A
B
C
D
(
(
(
如图,∠ACD是△ABC的一个外角
∴∠ACD=∠A+∠B
新知讲解
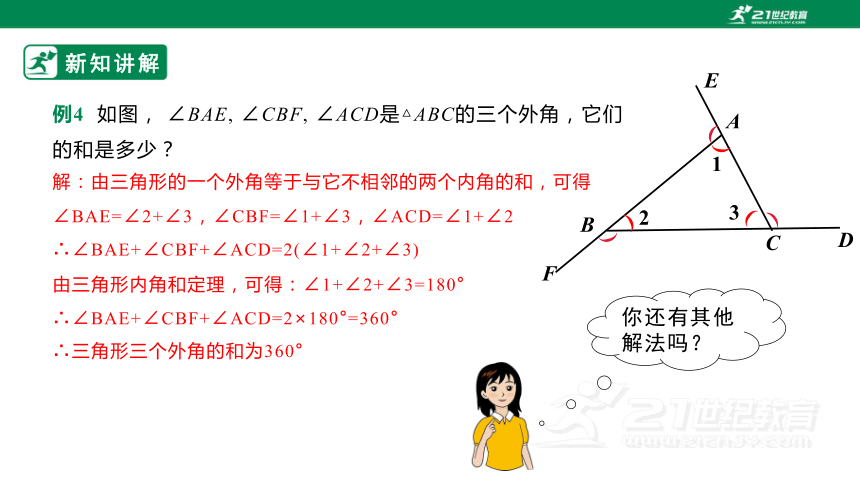
例4 如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:由三角形的一个外角等于与它不相邻的两个内角的和,可得
∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)
由三角形内角和定理,可得:∠1+∠2+∠3=180°
∴∠BAE+∠CBF+∠ACD=2×180°=360°
∴三角形三个外角的和为360°
你还有其他解法吗?
新知讲解
解法二:如图,∠BAE+∠1=180°,∠CBF+∠2=180°,∠ACD+∠3=180°
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=540°
又∠1+∠2+∠3=180°
∴∠BAE+∠CBF+∠ACD=360°
∴三角形三个外角的和为360°
三角形的外角和为360°
新知讲解
练 习
说出下列图形中∠1和∠2的读数。
(1) (2) (3)
1
1
1
2
2
2
60°
80°
30°
40°
40°
【解析】(1)∠1=180°-60°-80°=40°
∠2=80°+60°=140°
(2)∠1=180°-30°-40°=110°
∠2=30°+40°=70°
(3)∠1=180°-40°-90°=50°
∠2=50°+90°=140°
新知讲解
【解析】(4)∠2=180°-70°-40°=70°
∠ACD=70°+40°=110°
∵CE平分∠ACD
∴∠1= ∠ACD= ×110°=55°
(5)∠1=60°+20°=80°
∠2=180°-80°-60°=40°
(6)∠1=90°-30°=60°
∠2=90°-60°=30°
课堂练习
1、(2022·福建厦门·八年级期末)如图,在△ABC中,点D,E分别是边AB,BC上的点,连接AE和DE,则下列是△BDE的外角的是( )
A.∠AED B.∠AEC
C.∠ADE D.∠BAE
【解析】三角形的一个内角的一边与另一边的反向延长线所形成的夹角,称之为三角形的外角。因此△BDE的外角为∠ADE、∠DEC。故答案选C。
C
课堂练习
2、(2022·云南红河·八年级期末)如图,在△ABC中,D为线段BA延长线上一点,∠B=35°,∠DAC=60°,则∠C的度数为( )
A.85° B.45°
C.25° D.125°
【解析】∵∠DAC=∠B+∠C
∴∠C=∠DAC ∠B=60° 35°=25°
故答案选C
C
课堂练习
3、(2022·陕西西安·八年级期末)如图,已知l1∥l2,∠A=55°,∠2=100°,则∠1的度数为( )
A.50° B.55°
C.45° D.60°
【解析】∵l1∥l2
∴∠1=∠ABC
又∠A=55°,∠2=∠A+∠ABC=100°
∴∠ABC=∠2-∠A=100°-55°=45°
∴∠1=∠ABC=45°
故答案选C
C
课堂练习
4、(2022·河南郑州·八年级期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=__________。
【解析】∵BP是△ABC中∠ABC的平分线,
CP是∠ACB的外角的平分线
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°
∵∠PCM是△BCP的外角
∴∠P=∠PCM-∠CBP=50°-20°=30°
30°
课堂练习
5、(2022·湖南益阳·八年级期末)如图所示,平面上直线a、b分别过线段AB两端点,则a、b相交所成的锐角为_______度。
【解析】设a、b相交所成的锐角为x
∴80°+x=100°
解得:x=20°
即a、b相交所成的锐角为20°
30
课堂练习
6、(2022·贵州·遵义市新蒲新区天立学校八年级期中)如图,在△ABC中,∠B=50°,∠C=70°,AE是BC边上的高,AD平分∠BAC。
(1)求∠BAD的度数;
(1)解:∵在△ABC中,∠B=50°,∠C=70°
∴∠BAC=180°-∠B-∠C
=180°-50°-70°
=60°
∵AD平分∠BAC
∴∠BAD= ∠BAC= ×60°=30°
∴∠BAD的度数为30°
课堂练习
6、(2022·贵州·遵义市新蒲新区天立学校八年级期中)如图,在△ABC中,∠B=50°,∠C=70°,AE是BC边上的高,AD平分∠BAC。
(2)求∠EAD的度数。
(2)解:∵∠ADE是△ABD的外角
∴∠ADE=∠B+∠BAD
=50°+30°
=80°
∵AE是BC边上的高
∴∠DAE=90°-∠ADE
=90°-80°
=10°
∴∠EAD的度数为10°
课堂总结
三角形的外角等于与它不相邻的
两个内角的和。
三角形的外角和为360°
作业布置
1、(2022·江西吉安·八年级期末)如图,△ABC中,∠A=60°,E、D分别在AB和AC上,点F在ED的延长线上,BD平分∠ABC,EF∥BC,CF∥AB,∠F=50°,则∠BDC的度数为( )
A.105° B.95°
C.90° D.85°
【解析】∵CF∥AB,∠F=50°
∴∠AEF=∠F=50°
∵EF∥BC
∴∠ABC=∠AEF=50°
∵BD平分∠ABC
∴∠ABD= ∠ABC= ×50°=25°
∴∠BDC=∠A+∠ABD=60°+25°=85°
D
作业布置
2、(2022·广东·平洲一中八年级期中)将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①OE平分∠AOD;②∠AOC=∠BOD:③∠AOC-∠CEA=15°;④∠COB+∠AOD=180°。
A.1 B.2 C.3 D.4
【解析】如图,设OC与AB相交于点F
∵∠AOB=90°,∠COD=90°
∴∠AOB=∠COD
∴∠AOB-∠BOC=∠COD-∠BOC,即∠AOC=∠BOD
故②符合题意
作业布置
∵无法证明∠BOE=∠COE
∴无法证明∠AOE=∠DOE
∴无法证明OE平分∠AOD
故①不符合题意
∵∠A=30°
∴∠EFO=∠A+∠AOC=∠AOC+30°
∵∠C=45°
∴∠CEA=∠EFO-∠C=∠AOC-15°
∴∠AOC-∠CEA=15°
故③符合题意
∵∠AOB=90°,∠COD=90°
∴∠AOC+∠COB=90°,∠COB+∠BOD=90°
∴∠AOC+∠COB+∠COB+∠BOD=180°
即∠COB+∠AOD=180°
故④符合题
故答案选C。
作业布置
3、(2022·浙江湖州·八年级期末)如图,在△ABC中,AE是△ABC的角平分线,D是AE延长线上一点,DH⊥BC于点H.若∠B=30°,∠C=50°,则∠EDH=____________。
【解析】由三角形的外角性质知:∠HED=∠AEC=∠B+ ∠BAC
故∠B+ ∠BAC+∠EDH=90° ①
△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°
即: ∠C+ ∠B+ ∠BAC=90° ②
②-①,得:∠EDH= (∠C-∠B)= ×(50°-30°)=10°
∴∠EDH=10°
10°
作业布置
4、(2022·陕西咸阳·八年级期末)如图,已知△ABC为等腰直角三角形,∠C=90°,点D在边BC上,点E在CB的延长线上,连接AD、AE,
求证:(1)∠ADC>45°;
证明:(1)∵△ABC是等腰直角三角形,∠C=90°
∴∠ABC=45°
∵∠ADC是△ABD的一个外角
∴∠ADC>∠ABC
∴∠ADC>45°
作业布置
4、(2022·陕西咸阳·八年级期末)如图,已知△ABC为等腰直角三角形,∠C=90°,点D在边BC上,点E在CB的延长线上,连接AD、AE,
求证: (2)∠E<45°。
证明:(2)∵△ABC是等腰直角三角形,∠C=90°
∴∠ABC=45°
∵∠ABC是△ABE的一个外角,
∴∠ABC>∠E
∴∠E<45°
作业布置
5、(2022·贵州黔南·八年级期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=60°,∠C=20°。
(1)∠BAE的度数是______。
解:∵∠B+∠C+∠BAC = 180°
∴∠BAC = 180°-∠B-∠C
= 180°- 60°- 20°
= 100°
∵ AE平分∠BAC
∴∠BAE= ∠BAC= ×100°=50°
∴∠BAE的度数为50°
作业布置
5、(2022·贵州黔南·八年级期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=60°,∠C=20°。
(2)∠DAE的度数是______。
(2)解:∵AD⊥BC
∴∠ADE= 90°
而∠ADE=∠B+∠BAD
∠BAD= 90°-∠B= 90°- 60°=30°
∴∠DAE=∠BAE-∠BAD
= 50°- 30°
= 20°
∴∠DAE的度数为20°
作业布置
5、(2022·贵州黔南·八年级期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=60°,∠C=20°。
(3)探究:如果把条件∠B=60°,∠C=20°改成∠B-∠C=40°,你认为能得
出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由。
解:能得出∠DAE的度数
设∠C=x,则∠B=40°+x
∴∠BAC=(180°-40°-x-x)=140°-2x
∵AE平分∠BAC
∴∠BAE= ∠BAC=70°-x
∵AD⊥BC,∠B=40°+x
∴∠BAD=50°-x
∴∠DAE=∠BAE-∠BAD=(70°-x)-(50°-x)=20°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2.2三角形的外角
人教版八年级上册
第十一章 三角形
教学目标
1、在操作活动中,探索并了解三角形的外角的两条性质。
2、利用学过的定理论证这些性质。
3、能利用三角形的外角性质解决与外角有关的实际问题。
新知导入
B
D
C
A
O
●
40 °
70 °
?
●
●
●
一天,熊大、熊二发现光头强在O处砍树后,熊大打算用迂回的方式,先从A前进到C处,然后再折回到B处截住光头强逃跑的去路,而熊二则直接在A处拦截光头强,已知∠BAC=40° , ∠ABC=70°。则熊大从C处要转多少度角才能直达B处?
新知导入
思路分析:根据三角形内角和定理,可求得∠ACB;
再根据平角为180°可求得∠DCB。
解:由三角形定理可得,∠A+∠B+∠ACB=180°
∴∠ACB=180°-∠A-∠B
=180°-40°-70°
=70°
∵∠ACB+∠DCB=180°
∴∠DCB=180°-∠ACB
=180°-70°
=110°
∠DCB=110°,而∠A+∠B=110°,像∠DCB这样
的角有什么特征吗?它又具有什么性质呢?
是不是这样的角都具有上述的等量关系呢?
新知讲解
一、三角形的外角
如图,把△ABC的一边BC延长,得到∠ACD。像这样,三角形的 与另
一边的 组成的角,叫做三角形的外角。
延长线
一边
如图,∠ACD为△ABC的外角
新知讲解
根据三角形外角的定义,同学们能判断出一个三角形有多少个内角吗?
如图,画出△ABC的所有外角。
A
B
C
新知讲解
A
B
C
教 师 总 结
①每个顶点相对应都有2个外角
②这两个外角互为对顶角
③每个三角形都有6个外角
新知讲解
二、三角形的外角的性质
如图,在△ABC中,∠A=70°,∠B=60°。∠ACD是△ABC的一个外角。你能由∠A、∠B求出∠ACD吗?如果能,∠ACD与∠A、∠B有什么关系?
解:由三角形内角和定理可得,∠A+∠B+∠ACB=180°
∴∠ACB=180°-∠A-∠B
=180°-70°-60°
=50°
∵∠ACB+∠DCA=180°
∴∠DCA=180°-∠ACB
=180°-50°
=130°
∵∠A=70°,∠B=60°
∴∠A+∠B=130°
∴∠DCA=∠A+∠B
三角形的一个外角等于与它不相邻的两个内角之和。
新知讲解
验 证 结 论
A
B
D
C
已知:如图,△ABC,求证:∠ACD=∠A+∠B。
证明:由三角形内角和定理可得
∠A+∠B+∠ACB=180°
而∠ACB+∠ACD=180°
∴ ∠ACB+∠ACD =∠A+∠B+∠ACB
∴∠ACD=∠A+∠B
同学们,还可以用其他的
方法证明吗?
新知讲解
1
2
A
B
D
C
E
证明:过点C作CE∥AB
∴∠1=∠B(两直线平行,同位角相等)
∴∠2=∠A(两直线平行,内错角相等)
∵∠ACD=∠1+∠2
∴∠ACD=∠A+∠B
新知讲解
三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和。
几 何 语 言
A
B
C
D
(
(
(
如图,∠ACD是△ABC的一个外角
∴∠ACD=∠A+∠B
新知讲解
例4 如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:由三角形的一个外角等于与它不相邻的两个内角的和,可得
∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)
由三角形内角和定理,可得:∠1+∠2+∠3=180°
∴∠BAE+∠CBF+∠ACD=2×180°=360°
∴三角形三个外角的和为360°
你还有其他解法吗?
新知讲解
解法二:如图,∠BAE+∠1=180°,∠CBF+∠2=180°,∠ACD+∠3=180°
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=540°
又∠1+∠2+∠3=180°
∴∠BAE+∠CBF+∠ACD=360°
∴三角形三个外角的和为360°
三角形的外角和为360°
新知讲解
练 习
说出下列图形中∠1和∠2的读数。
(1) (2) (3)
1
1
1
2
2
2
60°
80°
30°
40°
40°
【解析】(1)∠1=180°-60°-80°=40°
∠2=80°+60°=140°
(2)∠1=180°-30°-40°=110°
∠2=30°+40°=70°
(3)∠1=180°-40°-90°=50°
∠2=50°+90°=140°
新知讲解
【解析】(4)∠2=180°-70°-40°=70°
∠ACD=70°+40°=110°
∵CE平分∠ACD
∴∠1= ∠ACD= ×110°=55°
(5)∠1=60°+20°=80°
∠2=180°-80°-60°=40°
(6)∠1=90°-30°=60°
∠2=90°-60°=30°
课堂练习
1、(2022·福建厦门·八年级期末)如图,在△ABC中,点D,E分别是边AB,BC上的点,连接AE和DE,则下列是△BDE的外角的是( )
A.∠AED B.∠AEC
C.∠ADE D.∠BAE
【解析】三角形的一个内角的一边与另一边的反向延长线所形成的夹角,称之为三角形的外角。因此△BDE的外角为∠ADE、∠DEC。故答案选C。
C
课堂练习
2、(2022·云南红河·八年级期末)如图,在△ABC中,D为线段BA延长线上一点,∠B=35°,∠DAC=60°,则∠C的度数为( )
A.85° B.45°
C.25° D.125°
【解析】∵∠DAC=∠B+∠C
∴∠C=∠DAC ∠B=60° 35°=25°
故答案选C
C
课堂练习
3、(2022·陕西西安·八年级期末)如图,已知l1∥l2,∠A=55°,∠2=100°,则∠1的度数为( )
A.50° B.55°
C.45° D.60°
【解析】∵l1∥l2
∴∠1=∠ABC
又∠A=55°,∠2=∠A+∠ABC=100°
∴∠ABC=∠2-∠A=100°-55°=45°
∴∠1=∠ABC=45°
故答案选C
C
课堂练习
4、(2022·河南郑州·八年级期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=__________。
【解析】∵BP是△ABC中∠ABC的平分线,
CP是∠ACB的外角的平分线
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°
∵∠PCM是△BCP的外角
∴∠P=∠PCM-∠CBP=50°-20°=30°
30°
课堂练习
5、(2022·湖南益阳·八年级期末)如图所示,平面上直线a、b分别过线段AB两端点,则a、b相交所成的锐角为_______度。
【解析】设a、b相交所成的锐角为x
∴80°+x=100°
解得:x=20°
即a、b相交所成的锐角为20°
30
课堂练习
6、(2022·贵州·遵义市新蒲新区天立学校八年级期中)如图,在△ABC中,∠B=50°,∠C=70°,AE是BC边上的高,AD平分∠BAC。
(1)求∠BAD的度数;
(1)解:∵在△ABC中,∠B=50°,∠C=70°
∴∠BAC=180°-∠B-∠C
=180°-50°-70°
=60°
∵AD平分∠BAC
∴∠BAD= ∠BAC= ×60°=30°
∴∠BAD的度数为30°
课堂练习
6、(2022·贵州·遵义市新蒲新区天立学校八年级期中)如图,在△ABC中,∠B=50°,∠C=70°,AE是BC边上的高,AD平分∠BAC。
(2)求∠EAD的度数。
(2)解:∵∠ADE是△ABD的外角
∴∠ADE=∠B+∠BAD
=50°+30°
=80°
∵AE是BC边上的高
∴∠DAE=90°-∠ADE
=90°-80°
=10°
∴∠EAD的度数为10°
课堂总结
三角形的外角等于与它不相邻的
两个内角的和。
三角形的外角和为360°
作业布置
1、(2022·江西吉安·八年级期末)如图,△ABC中,∠A=60°,E、D分别在AB和AC上,点F在ED的延长线上,BD平分∠ABC,EF∥BC,CF∥AB,∠F=50°,则∠BDC的度数为( )
A.105° B.95°
C.90° D.85°
【解析】∵CF∥AB,∠F=50°
∴∠AEF=∠F=50°
∵EF∥BC
∴∠ABC=∠AEF=50°
∵BD平分∠ABC
∴∠ABD= ∠ABC= ×50°=25°
∴∠BDC=∠A+∠ABD=60°+25°=85°
D
作业布置
2、(2022·广东·平洲一中八年级期中)将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①OE平分∠AOD;②∠AOC=∠BOD:③∠AOC-∠CEA=15°;④∠COB+∠AOD=180°。
A.1 B.2 C.3 D.4
【解析】如图,设OC与AB相交于点F
∵∠AOB=90°,∠COD=90°
∴∠AOB=∠COD
∴∠AOB-∠BOC=∠COD-∠BOC,即∠AOC=∠BOD
故②符合题意
作业布置
∵无法证明∠BOE=∠COE
∴无法证明∠AOE=∠DOE
∴无法证明OE平分∠AOD
故①不符合题意
∵∠A=30°
∴∠EFO=∠A+∠AOC=∠AOC+30°
∵∠C=45°
∴∠CEA=∠EFO-∠C=∠AOC-15°
∴∠AOC-∠CEA=15°
故③符合题意
∵∠AOB=90°,∠COD=90°
∴∠AOC+∠COB=90°,∠COB+∠BOD=90°
∴∠AOC+∠COB+∠COB+∠BOD=180°
即∠COB+∠AOD=180°
故④符合题
故答案选C。
作业布置
3、(2022·浙江湖州·八年级期末)如图,在△ABC中,AE是△ABC的角平分线,D是AE延长线上一点,DH⊥BC于点H.若∠B=30°,∠C=50°,则∠EDH=____________。
【解析】由三角形的外角性质知:∠HED=∠AEC=∠B+ ∠BAC
故∠B+ ∠BAC+∠EDH=90° ①
△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°
即: ∠C+ ∠B+ ∠BAC=90° ②
②-①,得:∠EDH= (∠C-∠B)= ×(50°-30°)=10°
∴∠EDH=10°
10°
作业布置
4、(2022·陕西咸阳·八年级期末)如图,已知△ABC为等腰直角三角形,∠C=90°,点D在边BC上,点E在CB的延长线上,连接AD、AE,
求证:(1)∠ADC>45°;
证明:(1)∵△ABC是等腰直角三角形,∠C=90°
∴∠ABC=45°
∵∠ADC是△ABD的一个外角
∴∠ADC>∠ABC
∴∠ADC>45°
作业布置
4、(2022·陕西咸阳·八年级期末)如图,已知△ABC为等腰直角三角形,∠C=90°,点D在边BC上,点E在CB的延长线上,连接AD、AE,
求证: (2)∠E<45°。
证明:(2)∵△ABC是等腰直角三角形,∠C=90°
∴∠ABC=45°
∵∠ABC是△ABE的一个外角,
∴∠ABC>∠E
∴∠E<45°
作业布置
5、(2022·贵州黔南·八年级期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=60°,∠C=20°。
(1)∠BAE的度数是______。
解:∵∠B+∠C+∠BAC = 180°
∴∠BAC = 180°-∠B-∠C
= 180°- 60°- 20°
= 100°
∵ AE平分∠BAC
∴∠BAE= ∠BAC= ×100°=50°
∴∠BAE的度数为50°
作业布置
5、(2022·贵州黔南·八年级期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=60°,∠C=20°。
(2)∠DAE的度数是______。
(2)解:∵AD⊥BC
∴∠ADE= 90°
而∠ADE=∠B+∠BAD
∠BAD= 90°-∠B= 90°- 60°=30°
∴∠DAE=∠BAE-∠BAD
= 50°- 30°
= 20°
∴∠DAE的度数为20°
作业布置
5、(2022·贵州黔南·八年级期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=60°,∠C=20°。
(3)探究:如果把条件∠B=60°,∠C=20°改成∠B-∠C=40°,你认为能得
出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由。
解:能得出∠DAE的度数
设∠C=x,则∠B=40°+x
∴∠BAC=(180°-40°-x-x)=140°-2x
∵AE平分∠BAC
∴∠BAE= ∠BAC=70°-x
∵AD⊥BC,∠B=40°+x
∴∠BAD=50°-x
∴∠DAE=∠BAE-∠BAD=(70°-x)-(50°-x)=20°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
