宁夏回族自治区银川三沙源上游高级中学校2022-2023学年高三上学期9月开学检测数学(文)试题(Word版含答案)
文档属性
| 名称 | 宁夏回族自治区银川三沙源上游高级中学校2022-2023学年高三上学期9月开学检测数学(文)试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览



文档简介
银川三沙源上游学校2022-2023学年第一学期开学检测
高三数学试题(文科)
时间:120分钟 分值:150分
班级:__________ 姓名:__________ 学号:__________
一、选择题(本题共12道小题,每小题5分,共60分)
1.,则下列式子中正确的是( )
A. B. C. D.
2.若命题,则对命题p的否定是( )
A.
B.
C.
D.
3.若.则( )
A. B. C. D.
4.函数单调递增区间是( )
A. B. C. D.
5.利用计算机产生0~1之间的均匀随机数a,则使关于x的一元二次方程无实根的概率为
( )
A. B. C. D.
6.样本数据的标准差为8,则数据的标准差为( )
A.8 B.15 C.16 D.32
7.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)如图所示:若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间上的运动员人数为( )
A.3 B.4 C.5 D.6
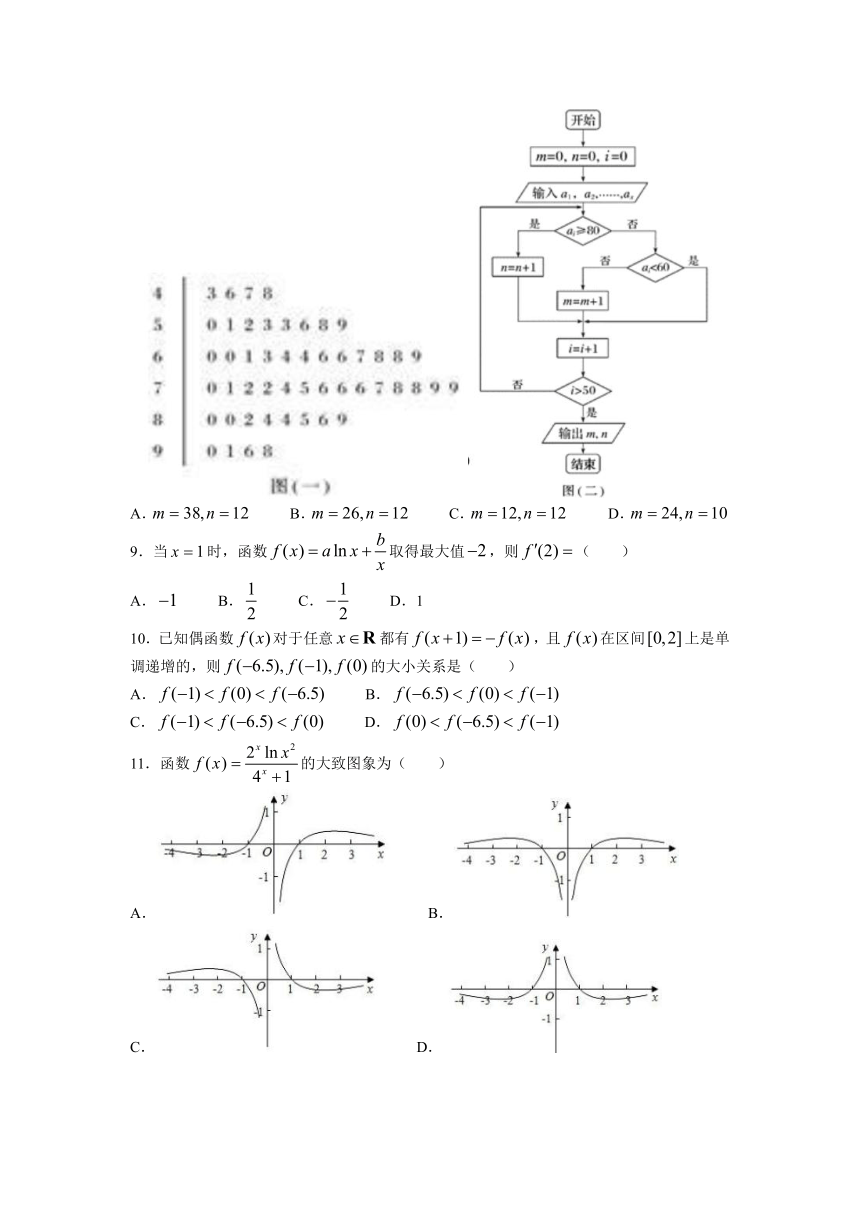
8.如图所示的茎叶图(图一)为高三某班50名学生的化学考试成绩,图(二)的算法框图中输入的a为茎叶图中的学生成绩,则输出的m,n分别是( )
A. B. C. D.
9.当时,函数取得最大值,则( )
A. B. C. D.1
10.已知偶函数对于任意都有,且在区间上是单调递增的,则的大小关系是( )
A. B.
C. D.
11.函数的大致图象为( )
A. B.
C. D.
12.已知,若函数有四个零点,则实数a的取值范围是( )
A. B. C. D.
二、填空题(本题共4道小题,每小题5分,共20分)
13.若复数z满足,则z的虚部为__________.
14.已知,式中变量x,y满足约束条件则z的最大值为__________.
15.从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为__________.
16.已知,函数在区间上的最大值是5,则a的取值范围是__________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
17.为进一步推进全国文明城市创建工作,营造浓厚的创建氛围,确保创建工作高质量达标.某市物业主管部门决定在市区住宅小区开展文明城市创建工作满意度测评,现从某小区居民中随机抽取若干人进行评分,绘制出如下的频率分布直方图(分组区间为),并将分数从低到高分为四个等级:
满意度评分
满意度等级 不满意 基本满意 满意 非常满意
(1)求表中a的值;若用A表示事件“满意度评分不低于80分”,将频率视为概率,求事件A发生的概率.
(2)若居民的满意指数不低于0.9,则该小区可获得“最美小区”称号.根据你所学的统计知识,判断该小区是否能获得“最美小区”称号?并说明理由.(注:满意指数)
18.2021年8月16日,中共中央政治局常务委员会召开会议,听取关于吉林长春长生公司问题疫苗案件调查及有关问责情况的汇报,中共中央总书记习近平主持会议并发表重要讲话.会议强调,疫苗关系人民群众健康,关系公共卫生安全和国家安全.因此,疫苗行业在生产、运输、储存、使用等任何一个环节都容不得半点瑕疵.国家规定,疫苗在上市前必须经过严格的检测,并通过临床实验获得相关数据,以保证疫苗使用的安全和有效.某生物制品研究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 感染病毒 总计
未注射疫苗 40 p x
注射疫苗 60 q y
总计 100 100 200
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为.
(1)求列联表中的数据p,q,x,y的值;
(2)能否有99.9%把握认为注射此种疫苗有效?
(3)在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例抽取5只进行病例分析,然后从这五只小白鼠中随机抽取3只对注射疫苗情况进行核实,求至少抽到2只为未注射疫苗的小白鼠的概率.
附:.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
19.足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x 2014 2015 2016 2017 2018
足球特色学校y(百个) 0.30 0.0 1.0 1.0 1.0
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:,则认为y与x线性相关性很强;,则认为y与x线性相关性一般;,则认为y与x线性相关性较弱):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据:.
,
20.已知函数,曲线在点处的切线为,当时,有极值.
(1)求a、b、c的值;
(2)求在上的最大值和最小值.
21.已知函数.
(Ⅰ)讨论函数的单调性;
(Ⅱ)对任意,求证:
(二)选考题:共10分.请考生在第22、23题中任选一题作答如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.在直角坐标系中,设倾斜角为的直线(t为参数)(t为参数)与曲线(为参数)相交于不同的两点A、B.
(1)若,求线段中点M的直角坐标;
(2)若,其中,求直线l的斜率.
23.选修4-5:不等式选讲
已知函数.
(1)当时,求不等式的解集;
(2)若时,恒成立,求实数a的取值范围.
银川三沙源上游学校2022-2023学年开学检测
高三数学答案(文科)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C A D C B C B B C D B B
二、填空题
13. 14.5 15.0.3 16.
三、解答题
17.(1)由频率分布直方图可知:
,
解得,
“满意度评分不低于80分”的频率为:.
因此,事件A发生的概率估计值为0.6.
(2)满意度的平均分为:,
所以居民的满意指数,
所以该小区不可获得“最美小区”称号.
18.(1)由题意,易得,
(2)由
得,
所以没有99.9%把握认为注射此种疫苗有效.
(3)由于在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例为3∶2,故抽取的5只小白鼠中3只未注射疫苗,用a,b,c表示,2只已注射疫苗,用D,E表示,从这五只小白鼠中随机抽取3只,可能的情况共有以下10种:.
其中至少抽到2只为未注射疫苗的小白鼠的情况有以下7种:
所以至少抽到2只为未注射疫苗的小白鼠的概率为.
19.(1)由题得
所以,∴y与x线性相关性很强.
(2),,
∴y关于x的线性回归方程是.当时,
,
即该地区2020年足球特色学校有244个.
20.(1)由,得,
当时,切线l的斜率为3,可得,①
当时,有极值,则
可得,②
由①②解得
由于切点的横坐标为,∴.∴.∴.
(2)由(1)可得,
∴.
令,得或.
当x变化时,y,的变化情况如下表:
x 1
+ 0 - 0 +
y 8 13 4
∴在上的最大值为13,最小值为
21.(Ⅰ)的定义域为R,
,
当时,恒成立,所以在R上单调递增;
当时,令,解得;令,解得,
所以在上单调递减,在上单调递增.
(Ⅱ)要证,即证,
即证,又,所以,即证.
令,则.
令,则,
易得在上单调递增,且,
所以存在唯一的实数,使得,
所以在上单调递减,在上单调递增.
因为,
所以当时,;当时,.
所以在上单调递减,在上单调递增,
所以.
综上.,即.
22.(1)当时,设点M对应参数为.直线l方程为(t为参数).
代入曲线C的普通方程,得,则,
所以,点M的坐标为.
(2)将代入,得
,
因为,所以.
得.由于,故.
所以直线l的斜率为.
23.(1)解:当时,
所以当时,,此时的解集为;
当时,,此时的解集为,
所以当时,求不等式的解集为
(2)解:因为当时,恒成立,
所以在上恒成立,
所以在上恒成立,
因为由绝对值三角不等式得:,
所以恒成立,即,解得.
所以实数a的取值范围是.
高三数学试题(文科)
时间:120分钟 分值:150分
班级:__________ 姓名:__________ 学号:__________
一、选择题(本题共12道小题,每小题5分,共60分)
1.,则下列式子中正确的是( )
A. B. C. D.
2.若命题,则对命题p的否定是( )
A.
B.
C.
D.
3.若.则( )
A. B. C. D.
4.函数单调递增区间是( )
A. B. C. D.
5.利用计算机产生0~1之间的均匀随机数a,则使关于x的一元二次方程无实根的概率为
( )
A. B. C. D.
6.样本数据的标准差为8,则数据的标准差为( )
A.8 B.15 C.16 D.32
7.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)如图所示:若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间上的运动员人数为( )
A.3 B.4 C.5 D.6
8.如图所示的茎叶图(图一)为高三某班50名学生的化学考试成绩,图(二)的算法框图中输入的a为茎叶图中的学生成绩,则输出的m,n分别是( )
A. B. C. D.
9.当时,函数取得最大值,则( )
A. B. C. D.1
10.已知偶函数对于任意都有,且在区间上是单调递增的,则的大小关系是( )
A. B.
C. D.
11.函数的大致图象为( )
A. B.
C. D.
12.已知,若函数有四个零点,则实数a的取值范围是( )
A. B. C. D.
二、填空题(本题共4道小题,每小题5分,共20分)
13.若复数z满足,则z的虚部为__________.
14.已知,式中变量x,y满足约束条件则z的最大值为__________.
15.从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为__________.
16.已知,函数在区间上的最大值是5,则a的取值范围是__________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
17.为进一步推进全国文明城市创建工作,营造浓厚的创建氛围,确保创建工作高质量达标.某市物业主管部门决定在市区住宅小区开展文明城市创建工作满意度测评,现从某小区居民中随机抽取若干人进行评分,绘制出如下的频率分布直方图(分组区间为),并将分数从低到高分为四个等级:
满意度评分
满意度等级 不满意 基本满意 满意 非常满意
(1)求表中a的值;若用A表示事件“满意度评分不低于80分”,将频率视为概率,求事件A发生的概率.
(2)若居民的满意指数不低于0.9,则该小区可获得“最美小区”称号.根据你所学的统计知识,判断该小区是否能获得“最美小区”称号?并说明理由.(注:满意指数)
18.2021年8月16日,中共中央政治局常务委员会召开会议,听取关于吉林长春长生公司问题疫苗案件调查及有关问责情况的汇报,中共中央总书记习近平主持会议并发表重要讲话.会议强调,疫苗关系人民群众健康,关系公共卫生安全和国家安全.因此,疫苗行业在生产、运输、储存、使用等任何一个环节都容不得半点瑕疵.国家规定,疫苗在上市前必须经过严格的检测,并通过临床实验获得相关数据,以保证疫苗使用的安全和有效.某生物制品研究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 感染病毒 总计
未注射疫苗 40 p x
注射疫苗 60 q y
总计 100 100 200
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为.
(1)求列联表中的数据p,q,x,y的值;
(2)能否有99.9%把握认为注射此种疫苗有效?
(3)在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例抽取5只进行病例分析,然后从这五只小白鼠中随机抽取3只对注射疫苗情况进行核实,求至少抽到2只为未注射疫苗的小白鼠的概率.
附:.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
19.足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x 2014 2015 2016 2017 2018
足球特色学校y(百个) 0.30 0.0 1.0 1.0 1.0
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:,则认为y与x线性相关性很强;,则认为y与x线性相关性一般;,则认为y与x线性相关性较弱):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据:.
,
20.已知函数,曲线在点处的切线为,当时,有极值.
(1)求a、b、c的值;
(2)求在上的最大值和最小值.
21.已知函数.
(Ⅰ)讨论函数的单调性;
(Ⅱ)对任意,求证:
(二)选考题:共10分.请考生在第22、23题中任选一题作答如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.在直角坐标系中,设倾斜角为的直线(t为参数)(t为参数)与曲线(为参数)相交于不同的两点A、B.
(1)若,求线段中点M的直角坐标;
(2)若,其中,求直线l的斜率.
23.选修4-5:不等式选讲
已知函数.
(1)当时,求不等式的解集;
(2)若时,恒成立,求实数a的取值范围.
银川三沙源上游学校2022-2023学年开学检测
高三数学答案(文科)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C A D C B C B B C D B B
二、填空题
13. 14.5 15.0.3 16.
三、解答题
17.(1)由频率分布直方图可知:
,
解得,
“满意度评分不低于80分”的频率为:.
因此,事件A发生的概率估计值为0.6.
(2)满意度的平均分为:,
所以居民的满意指数,
所以该小区不可获得“最美小区”称号.
18.(1)由题意,易得,
(2)由
得,
所以没有99.9%把握认为注射此种疫苗有效.
(3)由于在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例为3∶2,故抽取的5只小白鼠中3只未注射疫苗,用a,b,c表示,2只已注射疫苗,用D,E表示,从这五只小白鼠中随机抽取3只,可能的情况共有以下10种:.
其中至少抽到2只为未注射疫苗的小白鼠的情况有以下7种:
所以至少抽到2只为未注射疫苗的小白鼠的概率为.
19.(1)由题得
所以,∴y与x线性相关性很强.
(2),,
∴y关于x的线性回归方程是.当时,
,
即该地区2020年足球特色学校有244个.
20.(1)由,得,
当时,切线l的斜率为3,可得,①
当时,有极值,则
可得,②
由①②解得
由于切点的横坐标为,∴.∴.∴.
(2)由(1)可得,
∴.
令,得或.
当x变化时,y,的变化情况如下表:
x 1
+ 0 - 0 +
y 8 13 4
∴在上的最大值为13,最小值为
21.(Ⅰ)的定义域为R,
,
当时,恒成立,所以在R上单调递增;
当时,令,解得;令,解得,
所以在上单调递减,在上单调递增.
(Ⅱ)要证,即证,
即证,又,所以,即证.
令,则.
令,则,
易得在上单调递增,且,
所以存在唯一的实数,使得,
所以在上单调递减,在上单调递增.
因为,
所以当时,;当时,.
所以在上单调递减,在上单调递增,
所以.
综上.,即.
22.(1)当时,设点M对应参数为.直线l方程为(t为参数).
代入曲线C的普通方程,得,则,
所以,点M的坐标为.
(2)将代入,得
,
因为,所以.
得.由于,故.
所以直线l的斜率为.
23.(1)解:当时,
所以当时,,此时的解集为;
当时,,此时的解集为,
所以当时,求不等式的解集为
(2)解:因为当时,恒成立,
所以在上恒成立,
所以在上恒成立,
因为由绝对值三角不等式得:,
所以恒成立,即,解得.
所以实数a的取值范围是.
同课章节目录
