2022-2023学年北师大版八年级数学上册第1章勾股定理 单元达标测试题(含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册第1章勾股定理 单元达标测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览



文档简介
2022-2023学年北师大版八年级数学上册《第1章勾股定理》单元达标测试题(附答案)
一.选择题(共10小题,满分30分)
1.在Rt△ABC中,∠C=90°,且AB=10,BC=6,则AC等于( )
A.12 B.8 C.4 D.2
2.下列4组数据中,是勾股数的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.6,7,8
3.课间休息时,嘉嘉从教室窗户向外看,看到行人为从A处快速到达图书馆B处,直接从长方形草地中穿过.为保护草地,嘉嘉想在A处立一个标牌:“少走■米,踏之何忍?”如图,若AB=17米,BC=8米,则标牌上“■”处的数字是( )
A.6 B.8 C.10 D.11
4.下列各组数中,不是勾股数的是( )
A.9、12、15 B.5、12、13 C.8、15、17 D.12、18、22
5.直角△ABC的斜边为5,一条直角边为4,则此三角形的面积是( )
A.10 B.20 C.12 D.6
6.如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
A.225 B.200 C.150 D.无法计算
7.如图,一棵树(树干与地面垂直)高3.6米,在一次强台风中树被强风折断,倒下后的树顶C与树根A的距离为2.4米,则这棵树断裂处点B离地面的高度AB的值为( )
A.2.4米 B.2.6米 C.0.6米 D.1米
8.小颖的妈妈用如图的口杯喝花茶,由于吸管有点短,不小心斜滑到杯里,已知口杯的内径6cm,口杯内部高度9cm,要使吸管不斜滑到杯里,下列吸管最短的是( )cm.
A.9 B.10 C.11 D.12
9.已知在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,则下列条件不能判定△ABC为直角三角形的是( )
A.∠B=∠C﹣∠A B.a:b:c=3:4:5
C.c2+b2=a2 D.∠A:∠B:∠C=5:12:13
10.意大利著名画家达 芬奇用一张纸片剪拼出不一样的空洞,而两个空洞的面积是相等的,如图所示,证明了勾股定理,若设左边图中空白部分的面积为S1,右边图中空白部分的面积为S2,则下列对S1,S2所列等式不正确的是( )
A.S1=a2+b2+2ab B.S2=c2+ab
C.S1=S2 D.a2+b2=c2
二.填空题(共6小题,满分24分)
11.已知直角三角形的一直角边长为6,斜边长为10,则另一条直角边长为 .
12.如果一个直角三角形的两条边长分别为8和15,那么这个三角形的第三边长的平方为 .
13.在Rt△ACB中,∠C=90°,AD平分∠BAC交BC于点D.若AB=10,AC=6,BD=5,则点D到AB的距离是 .
14.如图,△ABC中,AB=AC=5,BC=6,则△ABC的面积是 .
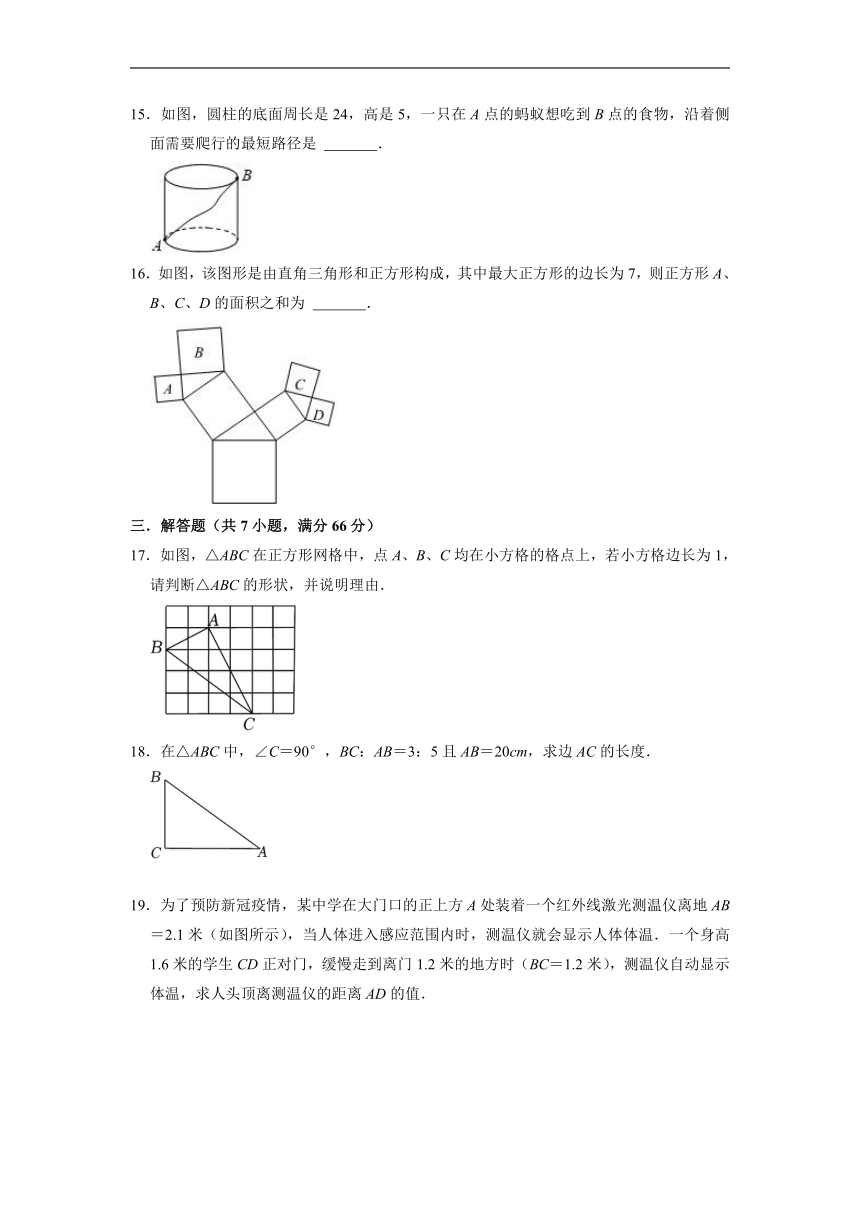
15.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁想吃到B点的食物,沿着侧面需要爬行的最短路径是 .
16.如图,该图形是由直角三角形和正方形构成,其中最大正方形的边长为7,则正方形A、B、C、D的面积之和为 .
三.解答题(共7小题,满分66分)
17.如图,△ABC在正方形网格中,点A、B、C均在小方格的格点上,若小方格边长为1,请判断△ABC的形状,并说明理由.
18.在△ABC中,∠C=90°,BC:AB=3:5且AB=20cm,求边AC的长度.
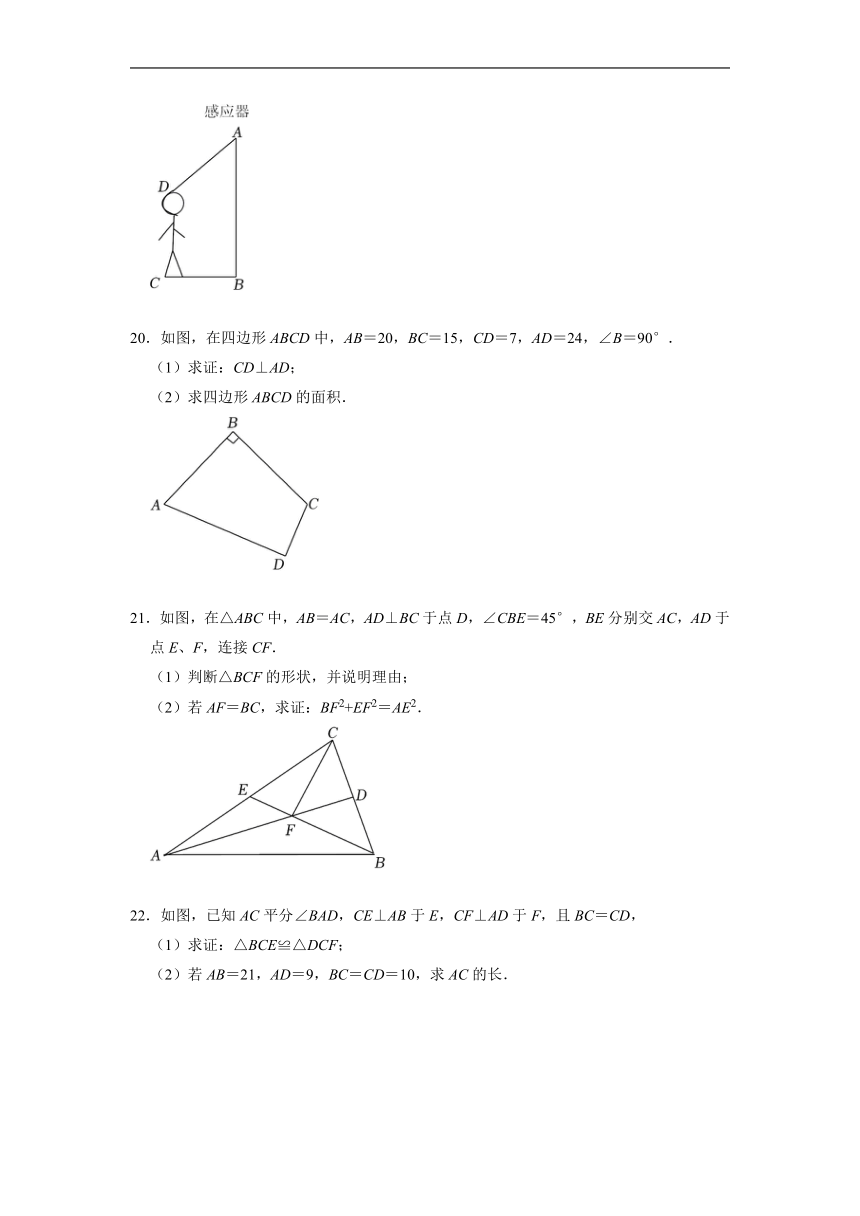
19.为了预防新冠疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地AB=2.1米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,求人头顶离测温仪的距离AD的值.
20.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)求证:CD⊥AD;
(2)求四边形ABCD的面积.
21.如图,在△ABC中,AB=AC,AD⊥BC于点D,∠CBE=45°,BE分别交AC,AD于点E、F,连接CF.
(1)判断△BCF的形状,并说明理由;
(2)若AF=BC,求证:BF2+EF2=AE2.
22.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求AC的长.
23.自2020年以来,安宁市建起了多个“口袋公园”,它们既美化了城市空间,又拓展了市民的公共活动场所,还体现着城市风貌和文化.如图,在某小区旁有一块四边形空地,其中∠B=90°,AB=20m,BC=15m,AD=24m,CD=7m.
(1)如图,连接AC,试求AC的长;
(2)安宁市委、市政府计划将其打造为“口袋公园”,经测算,每平方米的费用为2000元,请你计算将这块地打造成“口袋公园”需要多少钱.
参考答案
一.选择题(共10小题,满分30分)
1.解:由勾股定理得:AC=8,
故选:B.
2.解:A.12+22≠32,因此不是勾股数,故此选项不合题意;
B.22+32≠42,因此不是勾股数,故此选项不合题意;
C.32+42=52,因此是勾股数,故此选项符合题意;
D.62+72≠82,因此不是勾股数,故此选项不合题意;
故选:C.
3.解:在Rt△ABC中,由勾股定理得,
AC=15(米),
∴AC+BC﹣AB=15+8﹣17=6(米),
故选:A.
4.解:A.∵92+122=152,∴是勾股数,不符合题意;
B.∵52+122=132,∴是勾股数,不符合题意;
C.∵82+152=172,∴是勾股数,不符合题意;
D.∵122+182≠222,∴不是勾股数,符合题意;
故选:D.
5.解:由勾股定理得,另一条直角边为:3,
∴此三角形的面积是=6,
故选:D.
6.解:在Rt△ABC中,∠C=90°,
由勾股定理得,AC2+BC2=AB2=152=225,
∴正方形ADEC和正方形BCFG的面积和为225,
故选:A.
7.解:∵△ABC是直角三角形,AB+BC=3.6m,AC=2.4m,
∴BC2=AB2+AC2,
即(3.6﹣AB)2=AB2+2.42,
解得:AB=1,
故选:D.
8.解:如图,连接AB,
由题意知,BC=6cm,AC=9cm,
由勾股定理得,AB2=117,
∵117<121,
故选:C.
9.解:A.∵∠B=∠C﹣∠A,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵a:b:c=3:4:5,
∴设a=3k,b=4k,c=5k,
∴a2+b2=9k2+16k2=25k2,c2=25k2,
∴a2+b2=c2,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵c2+b2=a2,
∴△ABC是直角三角形,故本选项不符合题意;
D.∵∠A:∠B:∠C=5:12:13,∠A+∠B+∠C=180°,
∴最大角∠C的度数是180°×=78°<90°,
∴△ABC不是直角三角形,故本选项符合题意;
故选:D.
10.解:由勾股定理得:a2+b2=c2,
由题意得:S1=S2=a2+b2+2×ab=a2+b2+ab=c2+ab,
故选项A符合题意,选项B、C、D不符合题意,
故选:A.
二.填空题(共6小题,满分24分)
11.解:由勾股定理可得:
另一条直角边长的长度为:=8.
故答案为:8.
12.解:当8和15是两条直角边时,
第三边的平方=289,
当8和15分别是一斜边和一直角边时,
第三边的平方=161,
所以第三边的平方可能为161或289.
故答案为:161或289.
13.解:在Rt△ABC中,由勾股定理得,
BC=8,
∵BD=5,
∴CD=3,
过点D作DE⊥AB于E,
∵AD平分∠BAC,
∴CD=DE=3,
∴点D到AB的距离是3,
故答案为:3.
14.解:作AH⊥BC于H,
∵AB=AC,BC=6,
∴BH=BC=3,
由勾股定理得,AH=4,
∴△ABC的面积是==12,
故答案为:12.
15.解:展开圆柱的半个侧面是矩形,
矩形的长是圆柱的底面周长的一半,即为12,矩形的宽是圆柱的高5.
根据两点之间线段最短,
知最短路程是矩形的对角线的长,即=13,
故答案为:13.
16.解:如图,设正方形A,B,C,D,E,F的边长分别为a,b,c,d,e,f,
∵该图形是由直角三角形和正方形构成,
∴由勾股定理可得a2+b2=e2,c2+d2=f2,e2+f2=72,
∴a2+b2+c2+d2=72=49,
∴正方形A、B、C、D的面积之和为49,
故答案为:49.
三.解答题(共7小题,满分66分)
17.解:△ABC是直角三角形,
理由:由图可得,
∵AB2+AC2=BC2,
∴△ABC是直角三角形.
18.解:∵BC:AB=3:5,AB=20cm,
∴BC=12cm,
∵∠C=90°,
∴AC=16(cm),
答:边AC的长度为16cm.
19.解:如图,过点D作DE⊥AB于点E,
∵AB=2.1米,BE=CD=1.6米,ED=BC=1.2米,
∴AE=AB﹣BE=2.1﹣1.6=0.5(米).
在Rt△ADE中,由勾股定理得到:AD=1.3(米),
答:人头顶离测温仪的距离AD的值为1.3米.
20.(1)证明:连接AC,
∵∠B=90°,
∴AC2=BA2+BC2=400+225=625,
∵DA2+CD2=242+72=625,
∴AC2=DA2+DC2,
∴△ADC是直角三角形,即∠D是直角,
∴CD⊥AD;
(2)解:S四边形ABCD=S△ABC+S△ADC
=AB BC+AD CD
=×20×15+×24×7
=234.
21.(1)解:△BCF为等腰直角三角形.
理由:∵AB=AC,AD⊥BC,
∴BD=CD,
∴AD垂直平分BC,
∴BF=CF,
∴∠BCF=∠CBF=45°,
∴∠CFB=180°﹣45°﹣45°=90°,
∴△BCF为等腰直角三角形;
(2)证明:在BF上取一点H,使BH=EF,连接CH,
在△CHB和△AEF中,
,
∴△CHB≌△AEF(SAS),
∴AE=CH,∠AEF=∠BHC,
∴∠CEF=∠CHE,
∴CE=CH,
∵BD=CD,FD⊥BC,
∴CF=BF,
∴∠CFD=∠BFD=45°,
∴∠CFB=90°,
∴EF=FH,
Rt△CFH中,由勾股定理得:CF2+FH2=CH2,
∴BF2+EF2=AE2.
22.(1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴∠CFD=90°,∠CEB=90°(垂线的意义)
CE=CF(角平分线的性质)
∵BC=CD(已知)
∴Rt△BCE≌Rt△DCF(HL)
(2)解:由(1)得,
Rt△BCE≌Rt△DCF
∴DF=EB,设DF=EB=X
∵∠CFD=90°,∠CEB=90°,
CE=CF,AC=AC
∴Rt△AFC≌Rt△AEC(HL)
∴AF=AE
即:AD+DF=AB﹣BE
∵AB=21,AD=9,DF=EB=x
∴9+x=21﹣x解得,x=6
在Rt△DCF中,∵DF=6,CD=10
∴CF=8
∴Rt△AFC中,AC2=CF2+AF2=82+(9+6)2=289
∴AC=17
答:AC的长为17.
23.解:(1)∵∠B=90°,AB=20m,BC=15m,
∴AC=25(m),
答:AC的长为25m;
(2)∵AC2=625,CD2=49,AD2=576,
∴AC2=CD2+AD2,
∴△ACD是直角三角形,∠D=90°,
∴“口袋公园”的面积=S△ABC+S△ACD=AB×BC+×AD×CD=+24×7=234(m2),
234×2000=468000(元),
答:将这块地打造成“口袋公园”需要468000元钱.
一.选择题(共10小题,满分30分)
1.在Rt△ABC中,∠C=90°,且AB=10,BC=6,则AC等于( )
A.12 B.8 C.4 D.2
2.下列4组数据中,是勾股数的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.6,7,8
3.课间休息时,嘉嘉从教室窗户向外看,看到行人为从A处快速到达图书馆B处,直接从长方形草地中穿过.为保护草地,嘉嘉想在A处立一个标牌:“少走■米,踏之何忍?”如图,若AB=17米,BC=8米,则标牌上“■”处的数字是( )
A.6 B.8 C.10 D.11
4.下列各组数中,不是勾股数的是( )
A.9、12、15 B.5、12、13 C.8、15、17 D.12、18、22
5.直角△ABC的斜边为5,一条直角边为4,则此三角形的面积是( )
A.10 B.20 C.12 D.6
6.如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
A.225 B.200 C.150 D.无法计算
7.如图,一棵树(树干与地面垂直)高3.6米,在一次强台风中树被强风折断,倒下后的树顶C与树根A的距离为2.4米,则这棵树断裂处点B离地面的高度AB的值为( )
A.2.4米 B.2.6米 C.0.6米 D.1米
8.小颖的妈妈用如图的口杯喝花茶,由于吸管有点短,不小心斜滑到杯里,已知口杯的内径6cm,口杯内部高度9cm,要使吸管不斜滑到杯里,下列吸管最短的是( )cm.
A.9 B.10 C.11 D.12
9.已知在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,则下列条件不能判定△ABC为直角三角形的是( )
A.∠B=∠C﹣∠A B.a:b:c=3:4:5
C.c2+b2=a2 D.∠A:∠B:∠C=5:12:13
10.意大利著名画家达 芬奇用一张纸片剪拼出不一样的空洞,而两个空洞的面积是相等的,如图所示,证明了勾股定理,若设左边图中空白部分的面积为S1,右边图中空白部分的面积为S2,则下列对S1,S2所列等式不正确的是( )
A.S1=a2+b2+2ab B.S2=c2+ab
C.S1=S2 D.a2+b2=c2
二.填空题(共6小题,满分24分)
11.已知直角三角形的一直角边长为6,斜边长为10,则另一条直角边长为 .
12.如果一个直角三角形的两条边长分别为8和15,那么这个三角形的第三边长的平方为 .
13.在Rt△ACB中,∠C=90°,AD平分∠BAC交BC于点D.若AB=10,AC=6,BD=5,则点D到AB的距离是 .
14.如图,△ABC中,AB=AC=5,BC=6,则△ABC的面积是 .
15.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁想吃到B点的食物,沿着侧面需要爬行的最短路径是 .
16.如图,该图形是由直角三角形和正方形构成,其中最大正方形的边长为7,则正方形A、B、C、D的面积之和为 .
三.解答题(共7小题,满分66分)
17.如图,△ABC在正方形网格中,点A、B、C均在小方格的格点上,若小方格边长为1,请判断△ABC的形状,并说明理由.
18.在△ABC中,∠C=90°,BC:AB=3:5且AB=20cm,求边AC的长度.
19.为了预防新冠疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地AB=2.1米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,求人头顶离测温仪的距离AD的值.
20.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)求证:CD⊥AD;
(2)求四边形ABCD的面积.
21.如图,在△ABC中,AB=AC,AD⊥BC于点D,∠CBE=45°,BE分别交AC,AD于点E、F,连接CF.
(1)判断△BCF的形状,并说明理由;
(2)若AF=BC,求证:BF2+EF2=AE2.
22.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求AC的长.
23.自2020年以来,安宁市建起了多个“口袋公园”,它们既美化了城市空间,又拓展了市民的公共活动场所,还体现着城市风貌和文化.如图,在某小区旁有一块四边形空地,其中∠B=90°,AB=20m,BC=15m,AD=24m,CD=7m.
(1)如图,连接AC,试求AC的长;
(2)安宁市委、市政府计划将其打造为“口袋公园”,经测算,每平方米的费用为2000元,请你计算将这块地打造成“口袋公园”需要多少钱.
参考答案
一.选择题(共10小题,满分30分)
1.解:由勾股定理得:AC=8,
故选:B.
2.解:A.12+22≠32,因此不是勾股数,故此选项不合题意;
B.22+32≠42,因此不是勾股数,故此选项不合题意;
C.32+42=52,因此是勾股数,故此选项符合题意;
D.62+72≠82,因此不是勾股数,故此选项不合题意;
故选:C.
3.解:在Rt△ABC中,由勾股定理得,
AC=15(米),
∴AC+BC﹣AB=15+8﹣17=6(米),
故选:A.
4.解:A.∵92+122=152,∴是勾股数,不符合题意;
B.∵52+122=132,∴是勾股数,不符合题意;
C.∵82+152=172,∴是勾股数,不符合题意;
D.∵122+182≠222,∴不是勾股数,符合题意;
故选:D.
5.解:由勾股定理得,另一条直角边为:3,
∴此三角形的面积是=6,
故选:D.
6.解:在Rt△ABC中,∠C=90°,
由勾股定理得,AC2+BC2=AB2=152=225,
∴正方形ADEC和正方形BCFG的面积和为225,
故选:A.
7.解:∵△ABC是直角三角形,AB+BC=3.6m,AC=2.4m,
∴BC2=AB2+AC2,
即(3.6﹣AB)2=AB2+2.42,
解得:AB=1,
故选:D.
8.解:如图,连接AB,
由题意知,BC=6cm,AC=9cm,
由勾股定理得,AB2=117,
∵117<121,
故选:C.
9.解:A.∵∠B=∠C﹣∠A,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵a:b:c=3:4:5,
∴设a=3k,b=4k,c=5k,
∴a2+b2=9k2+16k2=25k2,c2=25k2,
∴a2+b2=c2,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵c2+b2=a2,
∴△ABC是直角三角形,故本选项不符合题意;
D.∵∠A:∠B:∠C=5:12:13,∠A+∠B+∠C=180°,
∴最大角∠C的度数是180°×=78°<90°,
∴△ABC不是直角三角形,故本选项符合题意;
故选:D.
10.解:由勾股定理得:a2+b2=c2,
由题意得:S1=S2=a2+b2+2×ab=a2+b2+ab=c2+ab,
故选项A符合题意,选项B、C、D不符合题意,
故选:A.
二.填空题(共6小题,满分24分)
11.解:由勾股定理可得:
另一条直角边长的长度为:=8.
故答案为:8.
12.解:当8和15是两条直角边时,
第三边的平方=289,
当8和15分别是一斜边和一直角边时,
第三边的平方=161,
所以第三边的平方可能为161或289.
故答案为:161或289.
13.解:在Rt△ABC中,由勾股定理得,
BC=8,
∵BD=5,
∴CD=3,
过点D作DE⊥AB于E,
∵AD平分∠BAC,
∴CD=DE=3,
∴点D到AB的距离是3,
故答案为:3.
14.解:作AH⊥BC于H,
∵AB=AC,BC=6,
∴BH=BC=3,
由勾股定理得,AH=4,
∴△ABC的面积是==12,
故答案为:12.
15.解:展开圆柱的半个侧面是矩形,
矩形的长是圆柱的底面周长的一半,即为12,矩形的宽是圆柱的高5.
根据两点之间线段最短,
知最短路程是矩形的对角线的长,即=13,
故答案为:13.
16.解:如图,设正方形A,B,C,D,E,F的边长分别为a,b,c,d,e,f,
∵该图形是由直角三角形和正方形构成,
∴由勾股定理可得a2+b2=e2,c2+d2=f2,e2+f2=72,
∴a2+b2+c2+d2=72=49,
∴正方形A、B、C、D的面积之和为49,
故答案为:49.
三.解答题(共7小题,满分66分)
17.解:△ABC是直角三角形,
理由:由图可得,
∵AB2+AC2=BC2,
∴△ABC是直角三角形.
18.解:∵BC:AB=3:5,AB=20cm,
∴BC=12cm,
∵∠C=90°,
∴AC=16(cm),
答:边AC的长度为16cm.
19.解:如图,过点D作DE⊥AB于点E,
∵AB=2.1米,BE=CD=1.6米,ED=BC=1.2米,
∴AE=AB﹣BE=2.1﹣1.6=0.5(米).
在Rt△ADE中,由勾股定理得到:AD=1.3(米),
答:人头顶离测温仪的距离AD的值为1.3米.
20.(1)证明:连接AC,
∵∠B=90°,
∴AC2=BA2+BC2=400+225=625,
∵DA2+CD2=242+72=625,
∴AC2=DA2+DC2,
∴△ADC是直角三角形,即∠D是直角,
∴CD⊥AD;
(2)解:S四边形ABCD=S△ABC+S△ADC
=AB BC+AD CD
=×20×15+×24×7
=234.
21.(1)解:△BCF为等腰直角三角形.
理由:∵AB=AC,AD⊥BC,
∴BD=CD,
∴AD垂直平分BC,
∴BF=CF,
∴∠BCF=∠CBF=45°,
∴∠CFB=180°﹣45°﹣45°=90°,
∴△BCF为等腰直角三角形;
(2)证明:在BF上取一点H,使BH=EF,连接CH,
在△CHB和△AEF中,
,
∴△CHB≌△AEF(SAS),
∴AE=CH,∠AEF=∠BHC,
∴∠CEF=∠CHE,
∴CE=CH,
∵BD=CD,FD⊥BC,
∴CF=BF,
∴∠CFD=∠BFD=45°,
∴∠CFB=90°,
∴EF=FH,
Rt△CFH中,由勾股定理得:CF2+FH2=CH2,
∴BF2+EF2=AE2.
22.(1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴∠CFD=90°,∠CEB=90°(垂线的意义)
CE=CF(角平分线的性质)
∵BC=CD(已知)
∴Rt△BCE≌Rt△DCF(HL)
(2)解:由(1)得,
Rt△BCE≌Rt△DCF
∴DF=EB,设DF=EB=X
∵∠CFD=90°,∠CEB=90°,
CE=CF,AC=AC
∴Rt△AFC≌Rt△AEC(HL)
∴AF=AE
即:AD+DF=AB﹣BE
∵AB=21,AD=9,DF=EB=x
∴9+x=21﹣x解得,x=6
在Rt△DCF中,∵DF=6,CD=10
∴CF=8
∴Rt△AFC中,AC2=CF2+AF2=82+(9+6)2=289
∴AC=17
答:AC的长为17.
23.解:(1)∵∠B=90°,AB=20m,BC=15m,
∴AC=25(m),
答:AC的长为25m;
(2)∵AC2=625,CD2=49,AD2=576,
∴AC2=CD2+AD2,
∴△ACD是直角三角形,∠D=90°,
∴“口袋公园”的面积=S△ABC+S△ACD=AB×BC+×AD×CD=+24×7=234(m2),
234×2000=468000(元),
答:将这块地打造成“口袋公园”需要468000元钱.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
