2021-2022学年鲁教版(五四制)六年级上册数学1.2展开与折叠学案(无答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级上册数学1.2展开与折叠学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 155.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览

文档简介
课题 1.2展开与折叠
学习目标 了解圆柱、圆锥的侧面展开图,能根据展开图判断立体模型,
学习策略 理解概念,掌握形式,主动探索
学习过程 复习巩固 1、棱柱的特点 (1)棱柱的上、下底面是___________________________. (2)棱柱的侧面都是______________. (3)棱柱的所有侧棱长都_____________. (4)棱柱各元素间的数量关系如下: 名称底面形状顶点数棱数侧棱数侧面数侧面形状总面数n棱柱
2、棱柱的分类 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱……长方体和正方体都是____________________. 3、圆柱的特点 (1)圆柱有_______ 个面 (2)圆柱的上下底面是__________,侧面是_____ 4、圆锥的特点 (1)圆锥有_____面 (2)圆锥的底面是______侧面是______
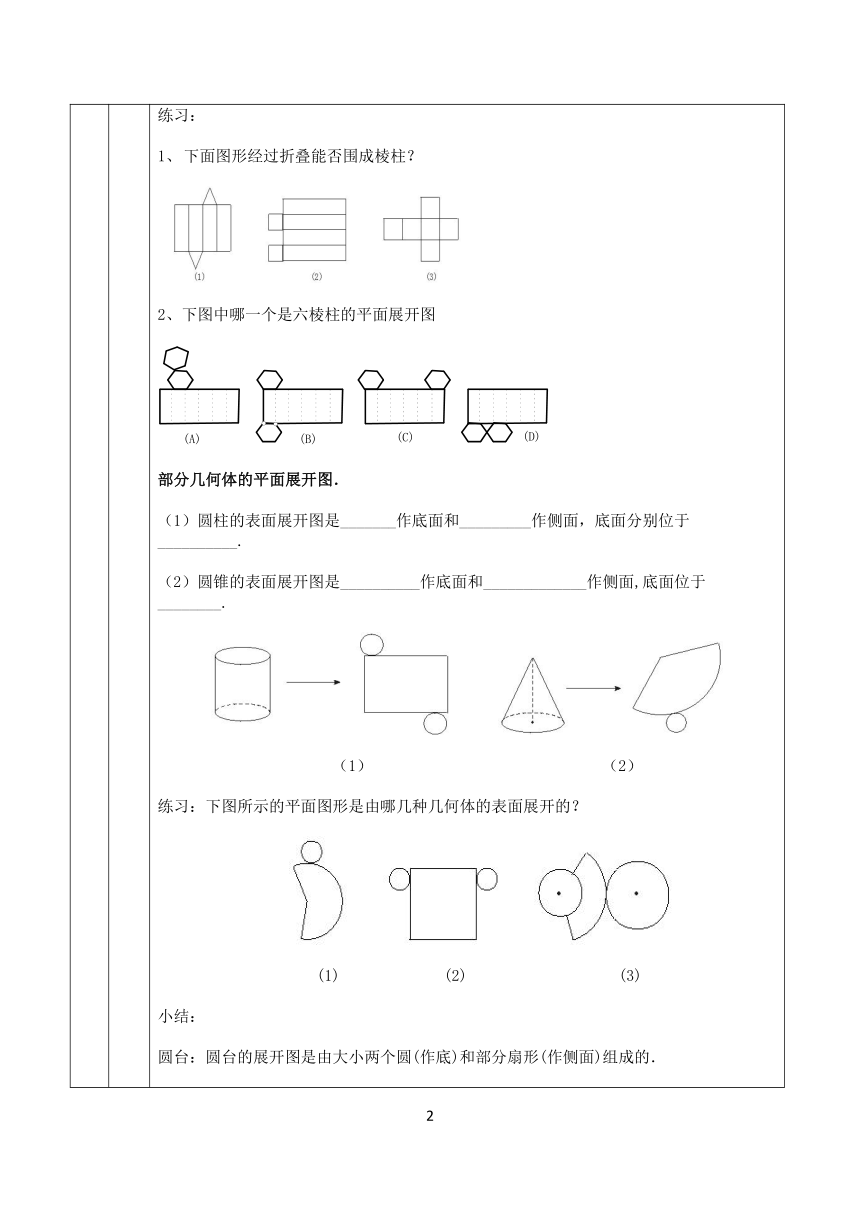
新课学习 想一想,再折一折,下面两图经过折叠能否围成棱柱? 总结:棱柱的展开图有____部分,侧面展开图是大_____包含___个小_________,上下底面的展开图是__________分别位于____________. 练习: 下面图形经过折叠能否围成棱柱? 2、下图中哪一个是六棱柱的平面展开图 部分几何体的平面展开图. (1)圆柱的表面展开图是_______作底面和_________作侧面,底面分别位于__________. (2)圆锥的表面展开图是__________作底面和_____________作侧面,底面位于________. (1) (2) 练习:下图所示的平面图形是由哪几种几何体的表面展开的? (1) (2) (3) 小结: 圆台:圆台的展开图是由大小两个圆(作底)和部分扇形(作侧面)组成的. 想一想 (1)如果将一个正方体沿某些棱剪开,展成一个平面图形,那么需要剪开______条棱。 (2)正方体表面展开图有几种?你能得到哪些平面图形?(画出来)
尝试应用 1.经过折叠不能围成一个正方体的图形是( ) 2. 小新准备用如图所示的纸片做一个礼品盒,为了美观,他想在六个正方形纸片上画上图案,使做成后三组对面的图案相同,那么画上的图案后正确的是( ) (
A.
B.
C.
D.
) 3. 下列各个平面图形中,属于圆锥的表面展开图的是( ) (A) (B) (C) (D) 4.某同学的茶杯是圆柱形,如图是茶杯的立体图,左边下方有一只蚂蚁,从A处爬行到对面的中点B处,如果蚂蚁爬行路线最短,请画出这条最短路线图。 (
B
)
自主总结 1. 小正方体纸盒沿某条棱任意剪开,可以得出11种不同的展开图。 2. 经历展开与折叠、模型制作等活动复原几何体。
达标测试 1.下面图形经过折叠不能围成棱柱( ) 2.如图,把左边的图形折叠起来,它会变成( ) 3.下面图形不能围成一个长方体的是( ) 4.如果有一个正方体,它的展开图可能是下面四个展开图中的( ) 5.用一个边长为4cm的正方形折叠围成一个四棱柱的侧面,若该四棱柱的底面是一个正方形,则此正方形边长为 cm. 6. .如图所示棱柱 (1)这个棱柱的底面是_____边形. (2)这个棱柱有_______个侧面,侧面的形状是_______边形. (3)侧面的个数与底面的边数_______.(填“相等”或“不 相等”) (4)这个棱柱有_______条侧棱,一共有_______条棱. (5)如果CC′=3 cm,那么BB′=_______cm. 7如下图,是边长为1 m的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请制作出实物模型,将正方体剪开,猜测蜘蛛爬行的最短路线. 8.下面平面图形能围成哪种几何体的表面.
1
学习目标 了解圆柱、圆锥的侧面展开图,能根据展开图判断立体模型,
学习策略 理解概念,掌握形式,主动探索
学习过程 复习巩固 1、棱柱的特点 (1)棱柱的上、下底面是___________________________. (2)棱柱的侧面都是______________. (3)棱柱的所有侧棱长都_____________. (4)棱柱各元素间的数量关系如下: 名称底面形状顶点数棱数侧棱数侧面数侧面形状总面数n棱柱
2、棱柱的分类 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱……长方体和正方体都是____________________. 3、圆柱的特点 (1)圆柱有_______ 个面 (2)圆柱的上下底面是__________,侧面是_____ 4、圆锥的特点 (1)圆锥有_____面 (2)圆锥的底面是______侧面是______
新课学习 想一想,再折一折,下面两图经过折叠能否围成棱柱? 总结:棱柱的展开图有____部分,侧面展开图是大_____包含___个小_________,上下底面的展开图是__________分别位于____________. 练习: 下面图形经过折叠能否围成棱柱? 2、下图中哪一个是六棱柱的平面展开图 部分几何体的平面展开图. (1)圆柱的表面展开图是_______作底面和_________作侧面,底面分别位于__________. (2)圆锥的表面展开图是__________作底面和_____________作侧面,底面位于________. (1) (2) 练习:下图所示的平面图形是由哪几种几何体的表面展开的? (1) (2) (3) 小结: 圆台:圆台的展开图是由大小两个圆(作底)和部分扇形(作侧面)组成的. 想一想 (1)如果将一个正方体沿某些棱剪开,展成一个平面图形,那么需要剪开______条棱。 (2)正方体表面展开图有几种?你能得到哪些平面图形?(画出来)
尝试应用 1.经过折叠不能围成一个正方体的图形是( ) 2. 小新准备用如图所示的纸片做一个礼品盒,为了美观,他想在六个正方形纸片上画上图案,使做成后三组对面的图案相同,那么画上的图案后正确的是( ) (
A.
B.
C.
D.
) 3. 下列各个平面图形中,属于圆锥的表面展开图的是( ) (A) (B) (C) (D) 4.某同学的茶杯是圆柱形,如图是茶杯的立体图,左边下方有一只蚂蚁,从A处爬行到对面的中点B处,如果蚂蚁爬行路线最短,请画出这条最短路线图。 (
B
)
自主总结 1. 小正方体纸盒沿某条棱任意剪开,可以得出11种不同的展开图。 2. 经历展开与折叠、模型制作等活动复原几何体。
达标测试 1.下面图形经过折叠不能围成棱柱( ) 2.如图,把左边的图形折叠起来,它会变成( ) 3.下面图形不能围成一个长方体的是( ) 4.如果有一个正方体,它的展开图可能是下面四个展开图中的( ) 5.用一个边长为4cm的正方形折叠围成一个四棱柱的侧面,若该四棱柱的底面是一个正方形,则此正方形边长为 cm. 6. .如图所示棱柱 (1)这个棱柱的底面是_____边形. (2)这个棱柱有_______个侧面,侧面的形状是_______边形. (3)侧面的个数与底面的边数_______.(填“相等”或“不 相等”) (4)这个棱柱有_______条侧棱,一共有_______条棱. (5)如果CC′=3 cm,那么BB′=_______cm. 7如下图,是边长为1 m的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请制作出实物模型,将正方体剪开,猜测蜘蛛爬行的最短路线. 8.下面平面图形能围成哪种几何体的表面.
1
