2022-2023学年苏科版八年级数学上册第2章轴对称图形 单元综合达标测试题(含解析)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册第2章轴对称图形 单元综合达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 301.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 13:56:42 | ||
图片预览


文档简介
2022-2023学年苏科版八年级数学上册《第2章轴对称图形》单元综合达标测试题(附答案)
一.选择题(共8小题,满分32分)
1.下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
2.下列说法错误的是( )
A.等边三角形有3条对称轴 B.正方形有4条对称轴
C.角的对称轴有2条 D.圆有无数条对称轴
3.下列条件中,不能得到等边三角形的是( )
A.有两个角是60°的三角形 B.有一个角是60°的等腰三角形
C.有两个外角相等的等腰三角形 D.三边都相等的三角形
4.到一个角的两边距离相等的点( )
A.在一条射线上 B.在两条互相垂直的射线上
C.在一条直线上 D.在两条互相垂直的直线上
5.如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )
A.30 B.33 C.36 D.39
6.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )
A.5cm B.10cm C.20cm D.15cm
7.边长为2和4的等腰三角形的周长为( )
A.8 B.10 C.12 D.8或10
8.如图,已知∠A=10°,在∠A两边上分别作点,并连接这些点,使AB=BC=CD=DE……一直作下去,那么图中以这些线段为腰长的等腰三角形最多能找到( )
A.7个 B.8个 C.9个 D.10个
二.填空题(共8小题,满分32分)
9.如图,是用一张长方形纸条折成的,如果∠1=63°,那么∠2= .
10.如图,在△ABC中,∠ACB=90°,AB=6,CD是AB边上的中线,则CD= .
11.如图,在△ABC中,AB=8,BC=6,AC的垂直平分MN交AB、AC于点M、N.则△BCM的周长为 .
12.等腰三角形ABC中∠A=50°,则∠B= .
13.如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD= .
14.在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD:DC=5:3,则D到AB的距离为 cm.
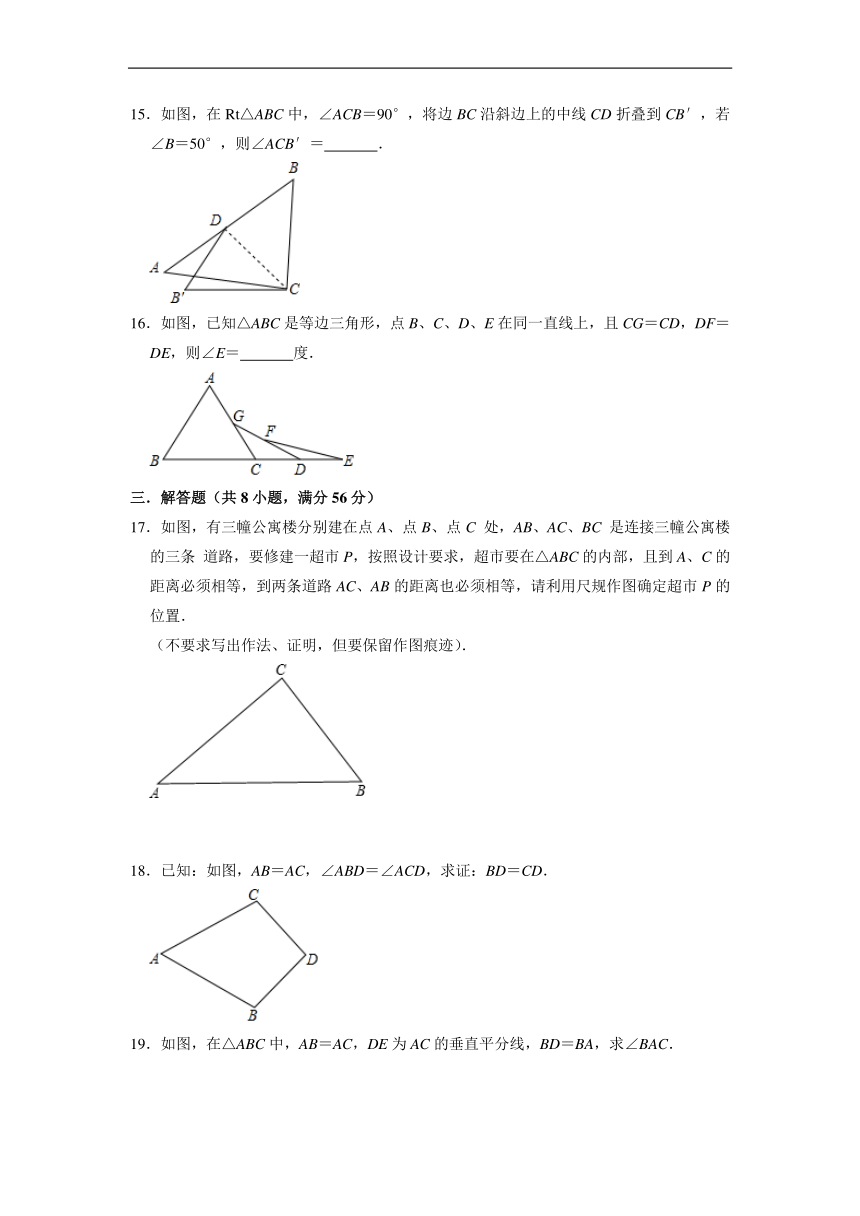
15.如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′= .
16.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 度.
三.解答题(共8小题,满分56分)
17.如图,有三幢公寓楼分别建在点A、点B、点C 处,AB、AC、BC 是连接三幢公寓楼的三条 道路,要修建一超市P,按照设计要求,超市要在△ABC的内部,且到A、C的距离必须相等,到两条道路AC、AB的距离也必须相等,请利用尺规作图确定超市P的位置.
(不要求写出作法、证明,但要保留作图痕迹).
18.已知:如图,AB=AC,∠ABD=∠ACD,求证:BD=CD.
19.如图,在△ABC中,AB=AC,DE为AC的垂直平分线,BD=BA,求∠BAC.
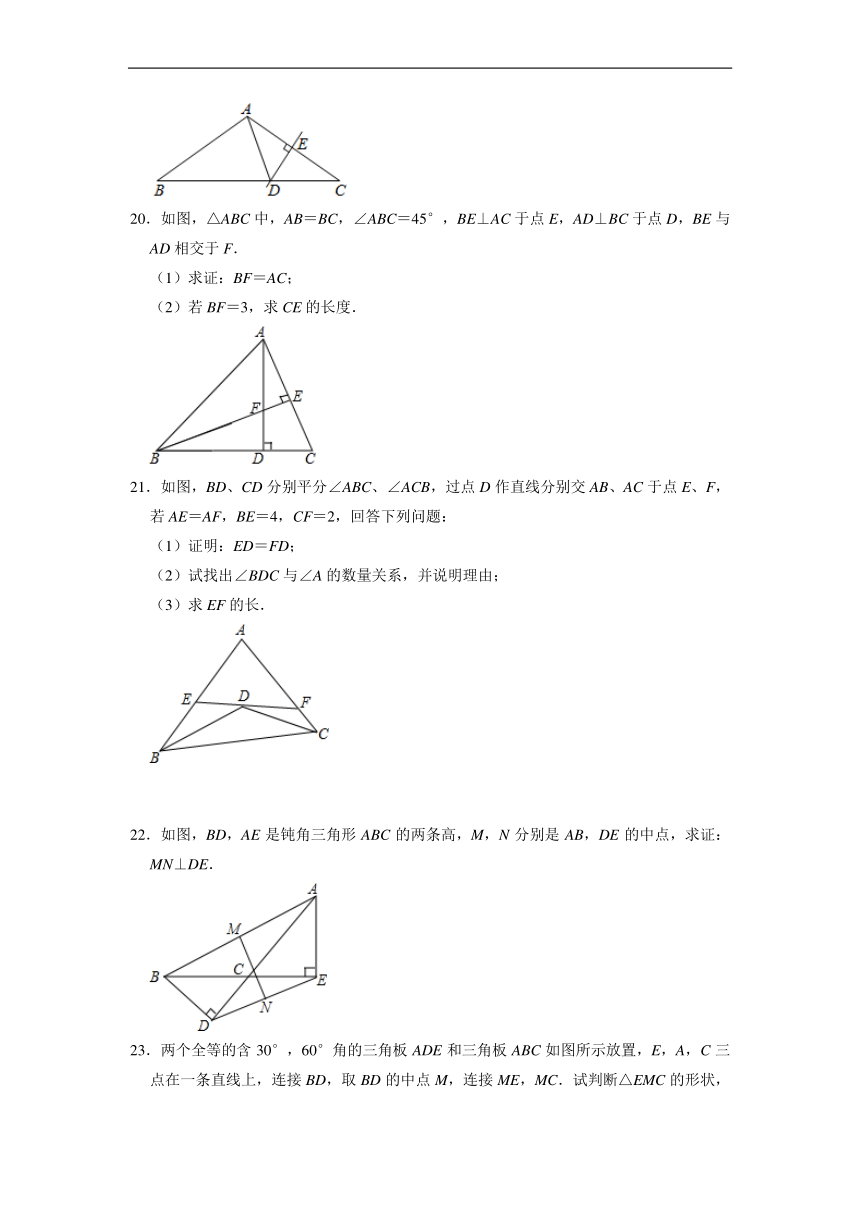
20.如图,△ABC中,AB=BC,∠ABC=45°,BE⊥AC于点E,AD⊥BC于点D,BE与AD相交于F.
(1)求证:BF=AC;
(2)若BF=3,求CE的长度.
21.如图,BD、CD分别平分∠ABC、∠ACB,过点D作直线分别交AB、AC于点E、F,若AE=AF,BE=4,CF=2,回答下列问题:
(1)证明:ED=FD;
(2)试找出∠BDC与∠A的数量关系,并说明理由;
(3)求EF的长.
22.如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE.
23.两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.
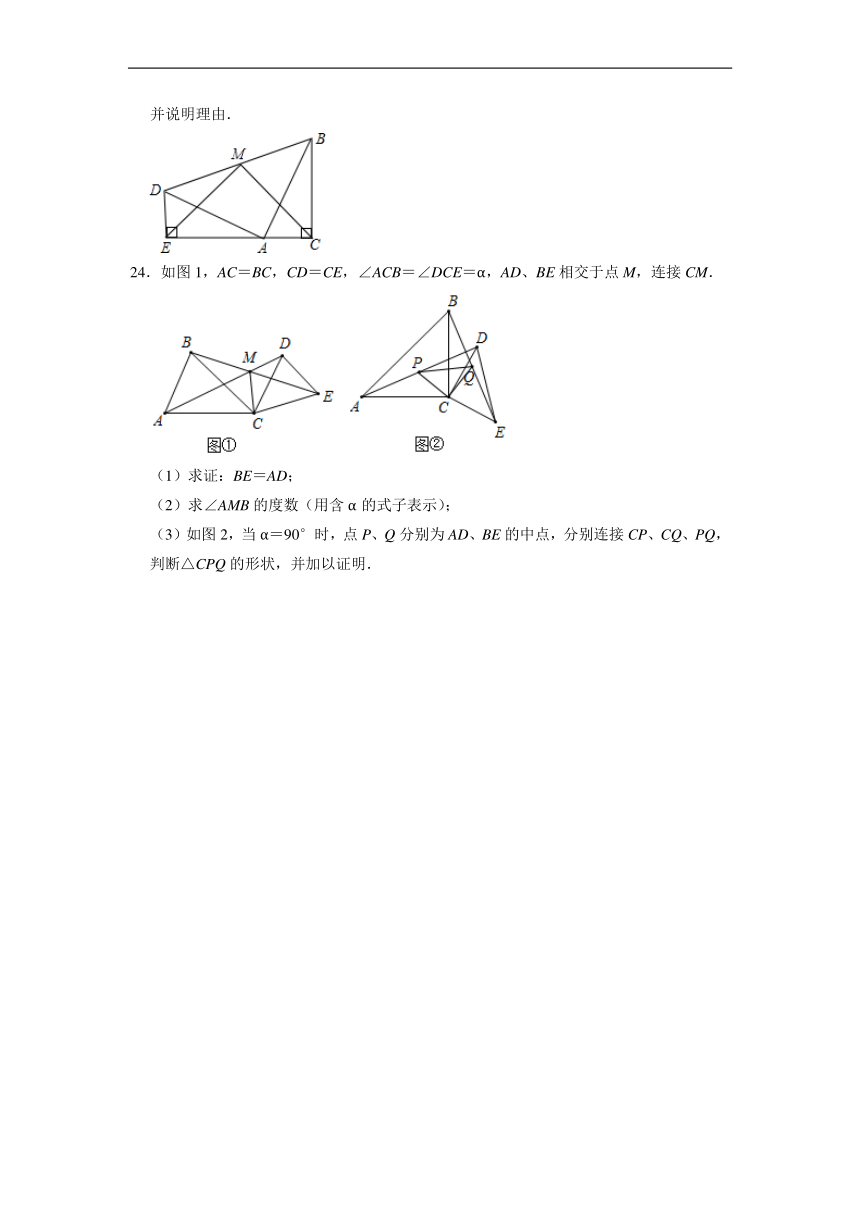
24.如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)求∠AMB的度数(用含α的式子表示);
(3)如图2,当α=90°时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断△CPQ的形状,并加以证明.
参考答案
一.选择题(共8小题,满分32分)
1.解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选:D.
2.解:A、等边三角形的对称轴是各边的中垂线,有3条,故正确;
B、正方形对称轴是边的中垂线与经过相对顶点的直线,共有4条,故选项正确;
C、角的对称轴是角的平分线所在的直线,只有一条,故错误;
D、圆的对称轴是经过圆心的直线,有无数条,故正确.
故选:C.
3.解:A、有两个角是60°的三角形,那么第三个角也是60°,故是等边三角形,正确;
B、有一个角是60°的等腰三角形是等边三角形,正确;
C、有两个外角相等的等腰三角形,不一定是等边三角形,故错误;
D、三边都相等的三角形是等腰三角形,正确;
故选:C.
4.解:到一个角的两边距离相等的点在这个角的角平分线所在直线上.
故选:C.
5.解:∵BO平分∠CBA,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵AB=12,AC=18,
∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30.
故选:A.
6.解:连接PG、PH,如图,
∵P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,
∴OM垂直平分PG,ON垂直平分PH,
∴AP=AG,BP=BH,
∴△PAB的周长=AP+AB+BP
=AG+AB+BH
=GH
=10cm.
故选:B.
7.解:①2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形,
②2是底边时,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10,
综上所述,它的周长为10.
故选:B.
8.解:∵AB=CB,∠A=10°,
∴∠CBD=∠CDB=20°,
…
从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是10°,第二个是20°,第三个是30°,四个是40°,五个是50°,六个是60°,七个是70°,八个是80°,九个是90°就不存在了.
所以一共有8个.
故选:B.
二.填空题(共8小题,满分32分)
9.解:∵2∠1+∠3=180°,∠1=63°,
∴∠3=54°.
∵长方形的上下两边平行,
∴∠2+∠3=180°,
∴∠2=180°﹣54°=126°.
故答案为:126°.
10.解:在Rt△ABC中,∠ACB=90°,AB=6,
∵CD是AB边上的中线,
∴CD=AB=3,
故答案为:3.
11.解:∵AC的垂直平分线MN交AB、AC于点M、N,
∴AM=CM.
∴△BCM的周长=BC+BM+CM=BC+AB=14.
故答案为:14.
12.解:已知等腰△ABC中,∠A=50°,
若∠A是顶角,则∠B=∠C,
所以∠B=(180°﹣50°)=65°;
若∠B是顶角,则∠A=∠C=50°,
所以∠B=180°﹣50°﹣50°=80°;
若∠C是顶角,则∠B=∠A=50°.
故∠B为65°或80°或50°,
故答案为:65°或80°或50°.
13.解:作PE⊥OB于E,
∵∠BOP=∠AOP,PD⊥OA,PE⊥OB,
∴PE=PD(角平分线上的点到角两边的距离相等),
∵∠BOP=∠AOP=15°,
∴∠AOB=30°,
∵PC∥OA,
∴∠BCP=∠AOB=30°,
∴在Rt△PCE中,PE=PC=×4=2(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴PD=PE=2,
故答案是:2.
14.解:如图,过点D作DE⊥AB于E,
∵BC=4cm,BD:DC=5:3,
∴CD=×4=1.5cm,
∵AD是∠BAC的平分线,
∴DE=CD=1.5cm.
故答案为:1.5.
15.解:∵∠ACB=90°,∠B=50°,
∴∠A=40°,
∵∠ACB=90°,CD是斜边上的中线,
∴CD=BD,CD=AD,
∴∠BCD=∠B=50°,∠DCA=∠A=40°,
由翻折变换的性质可知,∠B′CD=∠BCD=50°,
∴∠ACB′=∠B′CD﹣∠DCA=10°,
故答案为:10°.
16.解:∵△ABC是等边三角形,
∴∠C=∠A=60°,
∵CG=CD,
∴∠GDC=30°,
∵DF=DE,
∴∠E=15°.
故答案为:15.
三.解答题(共8小题,满分56分)
17.解:如图:
18.证明:连接BC.
∵AB=AC(已知),
∴∠1=∠2(等边对等角).
又∠ABD=∠ACD(已知),
∴∠ABD﹣∠1=∠ACD﹣∠2(等式运算性质).
即∠3=∠4.
∴BD=DC(等角对等边).
19.解:∵AB=AC,
∴∠B=∠C,
∵DE为AC的垂直平分线,
∴DA=DC,
∴∠C=∠DAC,
∵BD=BA,
∴∠BDA=∠BAD,
∵∠BDA是△ADC的一个外角,
∴∠BDA=∠C+∠DAC=2∠C=∠BAD,
在△ABC中,∠B+∠C+∠BAC=180°,
设∠C为x°,则有
x+x+2x+x=180°,
解得x=36°,
则∠BAC=2×36°+36°=108°.
20.解:如图所示:
(1)∵AD⊥BC,BE⊥AC,
∴∠FDB=∠FEA=∠ADC=90°,
又∵∠FDB+∠1+∠BFD=180°,
∠FEA+∠2+AFE=180°,
∠BFD=∠AFE,
∴∠1=∠2,
又∠ABC=45°,
∴BD=AD,
在△BDF和△ADC中,
,
∴△BDF≌△ADC(ASA)
∴BF=AC;
(2)∵BF=3,
∴AC=3,
又∵BE⊥AC,
∴CE=AE==.
21.(1)证明:过D点分别作DG⊥BC,DK⊥AB,DH⊥AC,垂足分别为G,K,H,如图,
∴∠EKD=∠FHD=90°,
∵BD平分∠ABC,CD平分∠ACB,
∴DK=DG=DH,
在△EKD和△FHD中,
,
∵AE=AF
∴∠AEF=∠AFE,
∴△EKD≌△FHD(AAS),
∴ED=FD;
(2)解:∠BDC=90°+∠A.
理由如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB),
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+(∠ABC+∠ACB)=180°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BDC+(180°﹣∠A)=180°,
∴∠BDC=90°+∠A;
(3)解:如图,
∵BD,CD分别平分∠ABC,∠ACB,
∴∠1=∠2,∠3=∠4,
∵∠2+∠7+∠4=180°,∠5+∠6+∠7=180°,
∴∠2+∠4=∠5+∠6,即∠1+∠3=∠5+∠6,
∵∠AEF=∠AFE,
∴∠1+∠5=∠3+∠6,
∴∠5=∠3,∠1=∠6,
∴△BED∽△CED,
∴ED:CF=BE:DF,
∵DE=DF,
则ED2=CF BE=2×4=8,
则ED=,
∴EF=2ED=.
22.证明:连接EM、MD,
∵BD,AE是钝角三角形ABC的两条高,
∴∠BEA=90°,∠BDA=90°,
∵M,N分别是AB,DE的中点,
∴DM=EM=AB,
∴△DME是等腰三角形,
∵N是DE中点,
∴MN⊥DE.
23.解:△EMC是等腰直角三角形.理由如下:
连接MA.
∵∠EAD=30°,∠BAC=60°,
∴∠DAB=90°,
∵△EDA≌△CAB,
∴DA=AB,ED=AC,
∴△DAB是等腰直角三角形.
又∵M为BD的中点,
∴∠MDA=∠MBA=45°,AM⊥BD(三线合一),
AM=BD=MD,(直角三角形斜边上的中线等于斜边的一半)
∴∠EDM=∠MAC=105°,
在△MDE和△CAM中,
ED=AC,∠MDE=∠CAM,MD=AM
∴△MDE≌△MAC.
∴∠DME=∠AMC,ME=MC,
又∵∠DMA=90°,
∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°.
∴△MEC是等腰直角三角形.
解法二:过点M作MF⊥EC于F.
∵DE⊥EC,MF⊥EC,BC⊥EC,
∴DE∥MF∥BC,
∵DM=BM,
∴EF=FC,
∴ME=MC,
∵MF=(DE+BC),DE=AC,BC=AE,
∴MF=EC,
∴FM=FE=FC,
∴∠EMC=90°,
∴△EMC是等腰直角三角形.
24.解:(1)如图1,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS)
∴BE=AD;
(2)如图1,∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵△ABC中,∠BAC+∠ABC=180°﹣α,
∴∠BAM+∠ABM=180°﹣α,
∴△ABM中,∠AMB=180°﹣(180°﹣α)=α;
(3)△CPQ为等腰直角三角形.
证明:如图2,由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
一.选择题(共8小题,满分32分)
1.下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
2.下列说法错误的是( )
A.等边三角形有3条对称轴 B.正方形有4条对称轴
C.角的对称轴有2条 D.圆有无数条对称轴
3.下列条件中,不能得到等边三角形的是( )
A.有两个角是60°的三角形 B.有一个角是60°的等腰三角形
C.有两个外角相等的等腰三角形 D.三边都相等的三角形
4.到一个角的两边距离相等的点( )
A.在一条射线上 B.在两条互相垂直的射线上
C.在一条直线上 D.在两条互相垂直的直线上
5.如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )
A.30 B.33 C.36 D.39
6.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )
A.5cm B.10cm C.20cm D.15cm
7.边长为2和4的等腰三角形的周长为( )
A.8 B.10 C.12 D.8或10
8.如图,已知∠A=10°,在∠A两边上分别作点,并连接这些点,使AB=BC=CD=DE……一直作下去,那么图中以这些线段为腰长的等腰三角形最多能找到( )
A.7个 B.8个 C.9个 D.10个
二.填空题(共8小题,满分32分)
9.如图,是用一张长方形纸条折成的,如果∠1=63°,那么∠2= .
10.如图,在△ABC中,∠ACB=90°,AB=6,CD是AB边上的中线,则CD= .
11.如图,在△ABC中,AB=8,BC=6,AC的垂直平分MN交AB、AC于点M、N.则△BCM的周长为 .
12.等腰三角形ABC中∠A=50°,则∠B= .
13.如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD= .
14.在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD:DC=5:3,则D到AB的距离为 cm.
15.如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′= .
16.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 度.
三.解答题(共8小题,满分56分)
17.如图,有三幢公寓楼分别建在点A、点B、点C 处,AB、AC、BC 是连接三幢公寓楼的三条 道路,要修建一超市P,按照设计要求,超市要在△ABC的内部,且到A、C的距离必须相等,到两条道路AC、AB的距离也必须相等,请利用尺规作图确定超市P的位置.
(不要求写出作法、证明,但要保留作图痕迹).
18.已知:如图,AB=AC,∠ABD=∠ACD,求证:BD=CD.
19.如图,在△ABC中,AB=AC,DE为AC的垂直平分线,BD=BA,求∠BAC.
20.如图,△ABC中,AB=BC,∠ABC=45°,BE⊥AC于点E,AD⊥BC于点D,BE与AD相交于F.
(1)求证:BF=AC;
(2)若BF=3,求CE的长度.
21.如图,BD、CD分别平分∠ABC、∠ACB,过点D作直线分别交AB、AC于点E、F,若AE=AF,BE=4,CF=2,回答下列问题:
(1)证明:ED=FD;
(2)试找出∠BDC与∠A的数量关系,并说明理由;
(3)求EF的长.
22.如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE.
23.两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.
24.如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)求∠AMB的度数(用含α的式子表示);
(3)如图2,当α=90°时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断△CPQ的形状,并加以证明.
参考答案
一.选择题(共8小题,满分32分)
1.解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选:D.
2.解:A、等边三角形的对称轴是各边的中垂线,有3条,故正确;
B、正方形对称轴是边的中垂线与经过相对顶点的直线,共有4条,故选项正确;
C、角的对称轴是角的平分线所在的直线,只有一条,故错误;
D、圆的对称轴是经过圆心的直线,有无数条,故正确.
故选:C.
3.解:A、有两个角是60°的三角形,那么第三个角也是60°,故是等边三角形,正确;
B、有一个角是60°的等腰三角形是等边三角形,正确;
C、有两个外角相等的等腰三角形,不一定是等边三角形,故错误;
D、三边都相等的三角形是等腰三角形,正确;
故选:C.
4.解:到一个角的两边距离相等的点在这个角的角平分线所在直线上.
故选:C.
5.解:∵BO平分∠CBA,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵AB=12,AC=18,
∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30.
故选:A.
6.解:连接PG、PH,如图,
∵P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,
∴OM垂直平分PG,ON垂直平分PH,
∴AP=AG,BP=BH,
∴△PAB的周长=AP+AB+BP
=AG+AB+BH
=GH
=10cm.
故选:B.
7.解:①2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形,
②2是底边时,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10,
综上所述,它的周长为10.
故选:B.
8.解:∵AB=CB,∠A=10°,
∴∠CBD=∠CDB=20°,
…
从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是10°,第二个是20°,第三个是30°,四个是40°,五个是50°,六个是60°,七个是70°,八个是80°,九个是90°就不存在了.
所以一共有8个.
故选:B.
二.填空题(共8小题,满分32分)
9.解:∵2∠1+∠3=180°,∠1=63°,
∴∠3=54°.
∵长方形的上下两边平行,
∴∠2+∠3=180°,
∴∠2=180°﹣54°=126°.
故答案为:126°.
10.解:在Rt△ABC中,∠ACB=90°,AB=6,
∵CD是AB边上的中线,
∴CD=AB=3,
故答案为:3.
11.解:∵AC的垂直平分线MN交AB、AC于点M、N,
∴AM=CM.
∴△BCM的周长=BC+BM+CM=BC+AB=14.
故答案为:14.
12.解:已知等腰△ABC中,∠A=50°,
若∠A是顶角,则∠B=∠C,
所以∠B=(180°﹣50°)=65°;
若∠B是顶角,则∠A=∠C=50°,
所以∠B=180°﹣50°﹣50°=80°;
若∠C是顶角,则∠B=∠A=50°.
故∠B为65°或80°或50°,
故答案为:65°或80°或50°.
13.解:作PE⊥OB于E,
∵∠BOP=∠AOP,PD⊥OA,PE⊥OB,
∴PE=PD(角平分线上的点到角两边的距离相等),
∵∠BOP=∠AOP=15°,
∴∠AOB=30°,
∵PC∥OA,
∴∠BCP=∠AOB=30°,
∴在Rt△PCE中,PE=PC=×4=2(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴PD=PE=2,
故答案是:2.
14.解:如图,过点D作DE⊥AB于E,
∵BC=4cm,BD:DC=5:3,
∴CD=×4=1.5cm,
∵AD是∠BAC的平分线,
∴DE=CD=1.5cm.
故答案为:1.5.
15.解:∵∠ACB=90°,∠B=50°,
∴∠A=40°,
∵∠ACB=90°,CD是斜边上的中线,
∴CD=BD,CD=AD,
∴∠BCD=∠B=50°,∠DCA=∠A=40°,
由翻折变换的性质可知,∠B′CD=∠BCD=50°,
∴∠ACB′=∠B′CD﹣∠DCA=10°,
故答案为:10°.
16.解:∵△ABC是等边三角形,
∴∠C=∠A=60°,
∵CG=CD,
∴∠GDC=30°,
∵DF=DE,
∴∠E=15°.
故答案为:15.
三.解答题(共8小题,满分56分)
17.解:如图:
18.证明:连接BC.
∵AB=AC(已知),
∴∠1=∠2(等边对等角).
又∠ABD=∠ACD(已知),
∴∠ABD﹣∠1=∠ACD﹣∠2(等式运算性质).
即∠3=∠4.
∴BD=DC(等角对等边).
19.解:∵AB=AC,
∴∠B=∠C,
∵DE为AC的垂直平分线,
∴DA=DC,
∴∠C=∠DAC,
∵BD=BA,
∴∠BDA=∠BAD,
∵∠BDA是△ADC的一个外角,
∴∠BDA=∠C+∠DAC=2∠C=∠BAD,
在△ABC中,∠B+∠C+∠BAC=180°,
设∠C为x°,则有
x+x+2x+x=180°,
解得x=36°,
则∠BAC=2×36°+36°=108°.
20.解:如图所示:
(1)∵AD⊥BC,BE⊥AC,
∴∠FDB=∠FEA=∠ADC=90°,
又∵∠FDB+∠1+∠BFD=180°,
∠FEA+∠2+AFE=180°,
∠BFD=∠AFE,
∴∠1=∠2,
又∠ABC=45°,
∴BD=AD,
在△BDF和△ADC中,
,
∴△BDF≌△ADC(ASA)
∴BF=AC;
(2)∵BF=3,
∴AC=3,
又∵BE⊥AC,
∴CE=AE==.
21.(1)证明:过D点分别作DG⊥BC,DK⊥AB,DH⊥AC,垂足分别为G,K,H,如图,
∴∠EKD=∠FHD=90°,
∵BD平分∠ABC,CD平分∠ACB,
∴DK=DG=DH,
在△EKD和△FHD中,
,
∵AE=AF
∴∠AEF=∠AFE,
∴△EKD≌△FHD(AAS),
∴ED=FD;
(2)解:∠BDC=90°+∠A.
理由如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB),
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+(∠ABC+∠ACB)=180°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BDC+(180°﹣∠A)=180°,
∴∠BDC=90°+∠A;
(3)解:如图,
∵BD,CD分别平分∠ABC,∠ACB,
∴∠1=∠2,∠3=∠4,
∵∠2+∠7+∠4=180°,∠5+∠6+∠7=180°,
∴∠2+∠4=∠5+∠6,即∠1+∠3=∠5+∠6,
∵∠AEF=∠AFE,
∴∠1+∠5=∠3+∠6,
∴∠5=∠3,∠1=∠6,
∴△BED∽△CED,
∴ED:CF=BE:DF,
∵DE=DF,
则ED2=CF BE=2×4=8,
则ED=,
∴EF=2ED=.
22.证明:连接EM、MD,
∵BD,AE是钝角三角形ABC的两条高,
∴∠BEA=90°,∠BDA=90°,
∵M,N分别是AB,DE的中点,
∴DM=EM=AB,
∴△DME是等腰三角形,
∵N是DE中点,
∴MN⊥DE.
23.解:△EMC是等腰直角三角形.理由如下:
连接MA.
∵∠EAD=30°,∠BAC=60°,
∴∠DAB=90°,
∵△EDA≌△CAB,
∴DA=AB,ED=AC,
∴△DAB是等腰直角三角形.
又∵M为BD的中点,
∴∠MDA=∠MBA=45°,AM⊥BD(三线合一),
AM=BD=MD,(直角三角形斜边上的中线等于斜边的一半)
∴∠EDM=∠MAC=105°,
在△MDE和△CAM中,
ED=AC,∠MDE=∠CAM,MD=AM
∴△MDE≌△MAC.
∴∠DME=∠AMC,ME=MC,
又∵∠DMA=90°,
∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°.
∴△MEC是等腰直角三角形.
解法二:过点M作MF⊥EC于F.
∵DE⊥EC,MF⊥EC,BC⊥EC,
∴DE∥MF∥BC,
∵DM=BM,
∴EF=FC,
∴ME=MC,
∵MF=(DE+BC),DE=AC,BC=AE,
∴MF=EC,
∴FM=FE=FC,
∴∠EMC=90°,
∴△EMC是等腰直角三角形.
24.解:(1)如图1,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS)
∴BE=AD;
(2)如图1,∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵△ABC中,∠BAC+∠ABC=180°﹣α,
∴∠BAM+∠ABM=180°﹣α,
∴△ABM中,∠AMB=180°﹣(180°﹣α)=α;
(3)△CPQ为等腰直角三角形.
证明:如图2,由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
