2022-2023学年人教版九年级数学上册21.3实际问题与一元二次方程 常考易错习题检测 (含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册21.3实际问题与一元二次方程 常考易错习题检测 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 164.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 14:18:28 | ||
图片预览




文档简介
2022-2023人教版九年级数学上册第二十一章
21.3实际问题与一元二次方程 常考易错习题检测 (附带答案)
一.选择题(共10小题)
1.小兵在暑假调查了某工厂得知,该工厂2020年全年某产品的产量为234万吨,经该厂的技术人员预计2022年全年该产品的产量为345万吨,设2020年至2022年该产品的预计年平均增长率为x,根据题意列出方程得( )
A.234(1+x)2=345 B.234(1﹣2x)=345
C.234(1+2x)=345 D.234(1﹣x)2=345
2.2022年北京冬奥会吉祥物“冰墩墩”意喻敦厚、健康、活泼、可爱,象征着冬奥会运动员强壮的身体、坚韧的意志和鼓舞人心的奥林匹克精神,随着北京冬奥会开幕日的临近,某特许零售店“冰墩墩”的销售日益火爆,据统计,该店2021年第四季度的“冰墩墩”总销售额为9.93万件,其中10月的销量为3万件,设11,12月份的平均增长率为x,则可列方程为( )
A.3(1+x)2=9.93 B.3+3(1+x)2=9.93
C.3+3x+3(1+x)2=9.93 D.3+3(1+x)+3(1+x)2=9.93
3.如图,在宽为20m,长为38m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
A.(20﹣x)(38﹣x)=540
B.(20﹣x)(38﹣x)=38×20﹣540
C.(20﹣2x)(38﹣2x)=540
D.(20﹣2x)(38﹣2x)=38×20﹣540
4.某小区原有一块长为50米,宽为40米的矩形健身场地,现计划在场内沿四周铺一圈宽度相等的小路,使小路所占的面积是原面积的,设这条小路的宽度为x米,则所列方程正确的是( )
A.2(50x+40x)=50×40×
B.(50﹣x)(40﹣x)=50×40×
C.(50+2x)(40+2x)=50×40×
D.(50﹣2x)(40﹣2x)=50×40×
5.某学校要组织一次篮球比赛,赛制为单循环形式(每两队之间都要赛一场),计划安排21场比赛,设参赛队数为x,列方程为( )
A.x(x﹣1)=21 B.x(x﹣1)=21
C.2x(x﹣1)=21 D.x(x+1)=21
6.空地上有一段长为a米的旧墙MN,利用旧墙和木栏围成一个矩形菜园(如图1或图2),已知木栏总长为40米,所围成的菜园面积为S.下列说法错误的是( )
A.若a=16,S=196,则有一种围法 B.若a=20,S=198,则有一种围法
C.若a=24,S=198,则有两种围法 D.若a=24,S=200,则有一种围法
7.在我市组织的一次青少年足球比赛预赛中,每两队之间都要进行一场比赛,共要比赛28场,则参赛队个数是( )
A.7 B.8 C.12 D.14
8.下表是某公司2022年1月份至5月份的收入统计表.其中,2月份和5月份被墨水污染.若2月份与3月份的增长率相同,设它们的增长率为x,根据表中的信息,可列方程为( )
月份 1 2 3 4 5
收入/万元 10 12 14
A.10(1+x)2=12﹣10 B.10(1+x)2=12
C.10(1+x)(1+2x)=12 D.10(1+x)3=14
9.一种病毒每轮传播的人数为x.若某人被感染后,未经有效防护,经过两轮传播共感染了144人,则x为( )
A.11 B.12 C.13 D.14
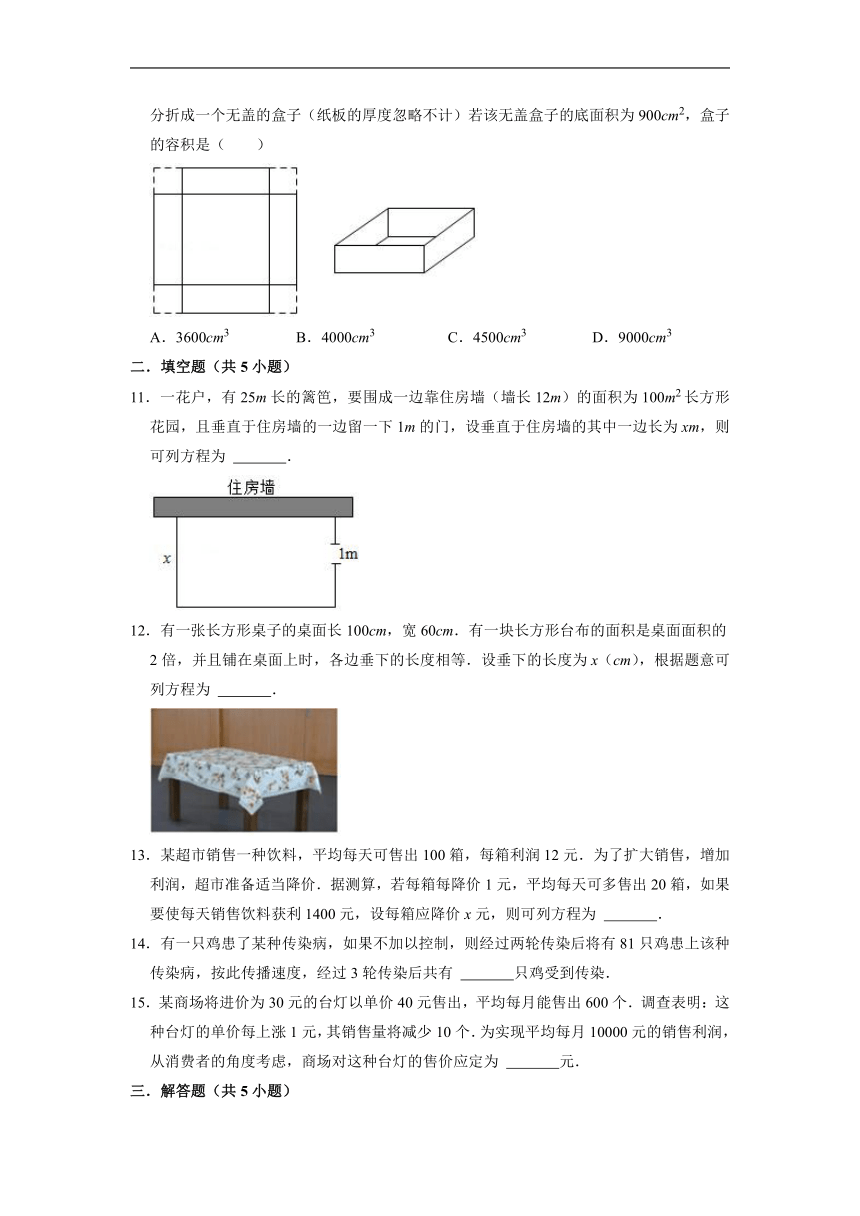
10.如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子(纸板的厚度忽略不计)若该无盖盒子的底面积为900cm2,盒子的容积是( )
A.3600cm3 B.4000cm3 C.4500cm3 D.9000cm3
二.填空题(共5小题)
11.一花户,有25m长的篱笆,要围成一边靠住房墙(墙长12m)的面积为100m2长方形花园,且垂直于住房墙的一边留一下1m的门,设垂直于住房墙的其中一边长为xm,则可列方程为 .
12.有一张长方形桌子的桌面长100cm,宽60cm.有一块长方形台布的面积是桌面面积的2倍,并且铺在桌面上时,各边垂下的长度相等.设垂下的长度为x(cm),根据题意可列方程为 .
13.某超市销售一种饮料,平均每天可售出100箱,每箱利润12元.为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱每降价1元,平均每天可多售出20箱,如果要使每天销售饮料获利1400元,设每箱应降价x元,则可列方程为 .
14.有一只鸡患了某种传染病,如果不加以控制,则经过两轮传染后将有81只鸡患上该种传染病,按此传播速度,经过3轮传染后共有 只鸡受到传染.
15.某商场将进价为30元的台灯以单价40元售出,平均每月能售出600个.调查表明:这种台灯的单价每上涨1元,其销售量将减少10个.为实现平均每月10000元的销售利润,从消费者的角度考虑,商场对这种台灯的售价应定为 元.
三.解答题(共5小题)
16.某一皮衣专卖店销售某款皮衣,其进价为每件750元,经市场调查发现,按每件1100元出售,平均每天可售出30件,每件降价50元,平均每天的销售量可增加10件,皮衣专卖店若想要平均每天获利12000元,则每件皮衣定价为多少元?
(1)以下是小明和小红的两种不同设法,请帮忙填完整:
小明:设每件皮衣降价x元,由题意,可列方程: .
小红:设每件皮衣定价为y元,由题意,可列方程: .
(2)请写出一种完整的解答过程.
17.某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图1、图2和图3所示(阴影部分为草坪).
请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图1,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
18.根据下列问题,列出关于x的方程,并将其化为一元二次方程的一般形式:
(1)如果一个直角三角形的两条直角边长之和为14cm,面积为24cm2,求它的两条直角边的长;
(2)有一个三位数,它的个位数字比十位数字大3,十位数字比百位数字小2,三个数字的平方和的9倍比这个三位数小20,求这个三位数.
19.某公司为了提高公司经济效益,进行了科技攻关.最近研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为45万元时,年销售量为550台;每台售价为50万元时,年销售量为500台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于65万元,如果该公司想获得12000万元的年利润,则该设备的销售单价应是多少万元?
20.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当Q到达点C时,点Q、P同时停止移动.
(1)如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积为4cm2?
(2)如果点P,Q分别从点A,B同时出发,那么几秒后,PQ的长度为5cm?
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据题意,得234(1+x)2=345,
故选:A.
2.【解答】解:根据题意,得3+3(1+x)+3(1+x)2=9.93.
故选:D.
3.【解答】解:∵小路宽为xm,
∴种植草坪的部分可合成长为(38﹣x)m,宽为(20﹣x)m的矩形.
依题意得:(20﹣x)(38﹣x)=540.
故选:A.
4.【解答】解:∵这条小路的宽度为x米,
∴小路围起来的部分是长为(50﹣2x)米、宽为(40﹣2x)米的矩形.
依题意得:(50﹣2x)(40﹣2x)=50×40×(1﹣).
故选:D.
5.【解答】解:根据题意,得,
故选:B.
6.【解答】解:如图,设矩形ABCD的边AB为x米,则宽BC为(40﹣2x)米,
根据题意得:S=(40﹣2x)x=﹣2x2+40x,
A、当a=16,S=196时,﹣2x2+40x=196,即x2﹣20x+98=0.
解得x1=10+,x2=10﹣,均符合题意,
所以图1有两种围法,故本选项说法错误,符合题意;
B、当a=20,S=198时,﹣2x2+40x=198,即x2﹣20x+99=0.
解得x1=9(不符合题意舍去),x2=11,
所以有一种围法,故本选项说法正确,不符合题意;
C、当a=24,S=198时,﹣2x2+40x=198,即x2﹣20x+99=0.
解得x1=11,x2=9,均符合题意,
所以有两种围法,故本选项说法正确,不符合题意;
D、当a=24,S=200时,﹣2x2+40x=200,即x2﹣20x+100=0.
解得x1=x2=10,符合题意,
所以有一种围法,故本选项说法正确,不符合题意;
故选:A.
7.【解答】解:设共有x支队伍参赛,
依题意得:x(x﹣1)=28,
整理得:x2﹣x﹣56=0,
解得:x1=8,x2=﹣7(不符合题意,舍去),
∴共有8支队伍参赛.
故选:B.
8.【解答】解:依题意得:10(1+x)2=12.
故选:B.
9.【解答】解:根据题意得:
1+x+x(x+1)=144,
解得x1=11,x2=﹣13(舍去),
故选:A.
10.【解答】解:设剪掉的正方形的边长为xcm,则做成的无盖盒子的底面为长(40﹣2x)cm的正方形,
依题意得:(40﹣2x)2=900,
解得:x1=5,x2=35(不合题意,舍去),
∴盒子的容积为900×5=4500(cm3).
故选:C.
二.填空题(共5小题)
11.【解答】解:设与墙垂直的一边长为xm,则与墙平行的一边长为(26﹣2x)m,
根据题意得:x(26﹣2x)=100.
故答案为:x(26﹣2x)=100.
12.【解答】解:∵垂下的长度为xcm,
∴台布的长为(100+2x)cm,宽为(60+2x)cm,
又∵台布的面积是桌面面积的2倍,
∴(100+2x)(60+2x)=2×100×60.
故答案为:(100+2x)(60+2x)=2×100×60.
13.【解答】解:设每箱应降价x元,商场日销售量(100+20x)箱,每箱饮料盈利(12﹣x)元;
依据题意列方程得,
(12﹣x)(100+20x)=1400,
故答案为:(12﹣x)(100+20x)=1400.
14.【解答】解:设每轮传染中1只鸡传染x只鸡,则第一轮传染中有x只鸡被传染,第二种传染中有x(1+x)只鸡被传染,
依题意得:1+x+x(1+x)=81,
整理得:(1+x)2=81,
解得:x1=8,x2=﹣10(不符合题意,舍去),
∴81+81x=81+81×8=729,
∴经过3轮传染后共有729只鸡受到传染.
故答案为:729.
15.【解答】解:设售价为x元,
根据题意得:(x﹣30)[600﹣10(x﹣40)]=10000,
解得:x=50或x=80,
从消费者的角度考虑,
x=80舍去,
答:这种台灯的售价应定为50元.
故答案为:50.
三.解答题(共5小题)
16.【解答】解:(1)小明:设每件皮衣降价x元,则平均每天的销售量为(30+x÷50×10)件,
依题意,得:(1100﹣x﹣750)(30+x÷50×10)=12000;
小红:设每件皮衣定价为y元,则平均每天的销售量为(30+×10)件,
依题意,得:(y﹣750)(30+)=12000.
故答案为:(1100﹣x﹣750)(30+x÷50×10)=12000;(y﹣750)(30+)=12000.
(2)选择小明的设法,则(1100﹣x﹣750)(30+x÷50×10)=12000,
整理,得:x2﹣200x+7500=0,
解得:x1=50,x2=150,
∴1100﹣x=1050或950.
答:每件皮衣定价为1050元或950元.
选择小红的设法,则(y﹣750)(30+)=12000,
整理,得:y2﹣2000y+997500=0,
解得:y1=1050,y2=950.
答:每件皮衣定价为1050元或950元.
17.【解答】解:①设道路的宽为x米.依题意得:
(35﹣2x)(20﹣2x)=600;
②设道路的宽为x米.依题意得:(35﹣x)(20﹣x)=600;
③设道路的宽为x米.依题意得:(35﹣2x)(20﹣x)=540.
18.【解答】解:(1)设其中一条直角边的长为xcm,则另一条直角边的长为(14﹣x)cm,
根据题意得x(14﹣x)=24,
整理得x2﹣14x+48=0.
(2)设十位数字为x,则个位数字为x+3,百位数字为x+2,
根据题意得:9[(x+3)2+x2+(x+2)2]﹣[100(x+2)+10x+(x+3)]=﹣20,
化简得9x2﹣7x﹣22=0.
19.【解答】解:(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),
将(45,550)、(50,500)代入y=kx+b,得:,
解得:,
故年销售量y与销售单价x的函数关系式为y=﹣10x+1000.
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,
根据题意得:(x﹣30)(﹣10x+1000)=12000,
整理,得:x2﹣130x+4200=0,
解得:x1=60,x2=70.
∵此设备的销售单价不得高于65万元,
∴x=60.
答:该设备的销售单价应是60万元/台.
20.【解答】解:当运动时间为ts时,AP=tcm,BP=(5﹣t)cm,BQ=2tcm.
(1)依题意得:(5﹣t)×2t=4,
整理得:t2﹣5t+4=0,
解得:t1=1,t2=4,
当t=1时,2t=2×1=2<7,符合题意;
当t=4时,2t=2×4=8>7,不符合题意,舍去.
答:1s后,△PBQ的面积为4cm2.
(2)依题意得:(5﹣t)2+(2t)2=25,
整理得:t2﹣2t=0,
解得:t1=0(不符合题意,舍去),t2=2.
答:2s后,PQ的长度为5cm
21.3实际问题与一元二次方程 常考易错习题检测 (附带答案)
一.选择题(共10小题)
1.小兵在暑假调查了某工厂得知,该工厂2020年全年某产品的产量为234万吨,经该厂的技术人员预计2022年全年该产品的产量为345万吨,设2020年至2022年该产品的预计年平均增长率为x,根据题意列出方程得( )
A.234(1+x)2=345 B.234(1﹣2x)=345
C.234(1+2x)=345 D.234(1﹣x)2=345
2.2022年北京冬奥会吉祥物“冰墩墩”意喻敦厚、健康、活泼、可爱,象征着冬奥会运动员强壮的身体、坚韧的意志和鼓舞人心的奥林匹克精神,随着北京冬奥会开幕日的临近,某特许零售店“冰墩墩”的销售日益火爆,据统计,该店2021年第四季度的“冰墩墩”总销售额为9.93万件,其中10月的销量为3万件,设11,12月份的平均增长率为x,则可列方程为( )
A.3(1+x)2=9.93 B.3+3(1+x)2=9.93
C.3+3x+3(1+x)2=9.93 D.3+3(1+x)+3(1+x)2=9.93
3.如图,在宽为20m,长为38m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
A.(20﹣x)(38﹣x)=540
B.(20﹣x)(38﹣x)=38×20﹣540
C.(20﹣2x)(38﹣2x)=540
D.(20﹣2x)(38﹣2x)=38×20﹣540
4.某小区原有一块长为50米,宽为40米的矩形健身场地,现计划在场内沿四周铺一圈宽度相等的小路,使小路所占的面积是原面积的,设这条小路的宽度为x米,则所列方程正确的是( )
A.2(50x+40x)=50×40×
B.(50﹣x)(40﹣x)=50×40×
C.(50+2x)(40+2x)=50×40×
D.(50﹣2x)(40﹣2x)=50×40×
5.某学校要组织一次篮球比赛,赛制为单循环形式(每两队之间都要赛一场),计划安排21场比赛,设参赛队数为x,列方程为( )
A.x(x﹣1)=21 B.x(x﹣1)=21
C.2x(x﹣1)=21 D.x(x+1)=21
6.空地上有一段长为a米的旧墙MN,利用旧墙和木栏围成一个矩形菜园(如图1或图2),已知木栏总长为40米,所围成的菜园面积为S.下列说法错误的是( )
A.若a=16,S=196,则有一种围法 B.若a=20,S=198,则有一种围法
C.若a=24,S=198,则有两种围法 D.若a=24,S=200,则有一种围法
7.在我市组织的一次青少年足球比赛预赛中,每两队之间都要进行一场比赛,共要比赛28场,则参赛队个数是( )
A.7 B.8 C.12 D.14
8.下表是某公司2022年1月份至5月份的收入统计表.其中,2月份和5月份被墨水污染.若2月份与3月份的增长率相同,设它们的增长率为x,根据表中的信息,可列方程为( )
月份 1 2 3 4 5
收入/万元 10 12 14
A.10(1+x)2=12﹣10 B.10(1+x)2=12
C.10(1+x)(1+2x)=12 D.10(1+x)3=14
9.一种病毒每轮传播的人数为x.若某人被感染后,未经有效防护,经过两轮传播共感染了144人,则x为( )
A.11 B.12 C.13 D.14
10.如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子(纸板的厚度忽略不计)若该无盖盒子的底面积为900cm2,盒子的容积是( )
A.3600cm3 B.4000cm3 C.4500cm3 D.9000cm3
二.填空题(共5小题)
11.一花户,有25m长的篱笆,要围成一边靠住房墙(墙长12m)的面积为100m2长方形花园,且垂直于住房墙的一边留一下1m的门,设垂直于住房墙的其中一边长为xm,则可列方程为 .
12.有一张长方形桌子的桌面长100cm,宽60cm.有一块长方形台布的面积是桌面面积的2倍,并且铺在桌面上时,各边垂下的长度相等.设垂下的长度为x(cm),根据题意可列方程为 .
13.某超市销售一种饮料,平均每天可售出100箱,每箱利润12元.为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱每降价1元,平均每天可多售出20箱,如果要使每天销售饮料获利1400元,设每箱应降价x元,则可列方程为 .
14.有一只鸡患了某种传染病,如果不加以控制,则经过两轮传染后将有81只鸡患上该种传染病,按此传播速度,经过3轮传染后共有 只鸡受到传染.
15.某商场将进价为30元的台灯以单价40元售出,平均每月能售出600个.调查表明:这种台灯的单价每上涨1元,其销售量将减少10个.为实现平均每月10000元的销售利润,从消费者的角度考虑,商场对这种台灯的售价应定为 元.
三.解答题(共5小题)
16.某一皮衣专卖店销售某款皮衣,其进价为每件750元,经市场调查发现,按每件1100元出售,平均每天可售出30件,每件降价50元,平均每天的销售量可增加10件,皮衣专卖店若想要平均每天获利12000元,则每件皮衣定价为多少元?
(1)以下是小明和小红的两种不同设法,请帮忙填完整:
小明:设每件皮衣降价x元,由题意,可列方程: .
小红:设每件皮衣定价为y元,由题意,可列方程: .
(2)请写出一种完整的解答过程.
17.某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图1、图2和图3所示(阴影部分为草坪).
请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图1,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
18.根据下列问题,列出关于x的方程,并将其化为一元二次方程的一般形式:
(1)如果一个直角三角形的两条直角边长之和为14cm,面积为24cm2,求它的两条直角边的长;
(2)有一个三位数,它的个位数字比十位数字大3,十位数字比百位数字小2,三个数字的平方和的9倍比这个三位数小20,求这个三位数.
19.某公司为了提高公司经济效益,进行了科技攻关.最近研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为45万元时,年销售量为550台;每台售价为50万元时,年销售量为500台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于65万元,如果该公司想获得12000万元的年利润,则该设备的销售单价应是多少万元?
20.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当Q到达点C时,点Q、P同时停止移动.
(1)如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积为4cm2?
(2)如果点P,Q分别从点A,B同时出发,那么几秒后,PQ的长度为5cm?
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据题意,得234(1+x)2=345,
故选:A.
2.【解答】解:根据题意,得3+3(1+x)+3(1+x)2=9.93.
故选:D.
3.【解答】解:∵小路宽为xm,
∴种植草坪的部分可合成长为(38﹣x)m,宽为(20﹣x)m的矩形.
依题意得:(20﹣x)(38﹣x)=540.
故选:A.
4.【解答】解:∵这条小路的宽度为x米,
∴小路围起来的部分是长为(50﹣2x)米、宽为(40﹣2x)米的矩形.
依题意得:(50﹣2x)(40﹣2x)=50×40×(1﹣).
故选:D.
5.【解答】解:根据题意,得,
故选:B.
6.【解答】解:如图,设矩形ABCD的边AB为x米,则宽BC为(40﹣2x)米,
根据题意得:S=(40﹣2x)x=﹣2x2+40x,
A、当a=16,S=196时,﹣2x2+40x=196,即x2﹣20x+98=0.
解得x1=10+,x2=10﹣,均符合题意,
所以图1有两种围法,故本选项说法错误,符合题意;
B、当a=20,S=198时,﹣2x2+40x=198,即x2﹣20x+99=0.
解得x1=9(不符合题意舍去),x2=11,
所以有一种围法,故本选项说法正确,不符合题意;
C、当a=24,S=198时,﹣2x2+40x=198,即x2﹣20x+99=0.
解得x1=11,x2=9,均符合题意,
所以有两种围法,故本选项说法正确,不符合题意;
D、当a=24,S=200时,﹣2x2+40x=200,即x2﹣20x+100=0.
解得x1=x2=10,符合题意,
所以有一种围法,故本选项说法正确,不符合题意;
故选:A.
7.【解答】解:设共有x支队伍参赛,
依题意得:x(x﹣1)=28,
整理得:x2﹣x﹣56=0,
解得:x1=8,x2=﹣7(不符合题意,舍去),
∴共有8支队伍参赛.
故选:B.
8.【解答】解:依题意得:10(1+x)2=12.
故选:B.
9.【解答】解:根据题意得:
1+x+x(x+1)=144,
解得x1=11,x2=﹣13(舍去),
故选:A.
10.【解答】解:设剪掉的正方形的边长为xcm,则做成的无盖盒子的底面为长(40﹣2x)cm的正方形,
依题意得:(40﹣2x)2=900,
解得:x1=5,x2=35(不合题意,舍去),
∴盒子的容积为900×5=4500(cm3).
故选:C.
二.填空题(共5小题)
11.【解答】解:设与墙垂直的一边长为xm,则与墙平行的一边长为(26﹣2x)m,
根据题意得:x(26﹣2x)=100.
故答案为:x(26﹣2x)=100.
12.【解答】解:∵垂下的长度为xcm,
∴台布的长为(100+2x)cm,宽为(60+2x)cm,
又∵台布的面积是桌面面积的2倍,
∴(100+2x)(60+2x)=2×100×60.
故答案为:(100+2x)(60+2x)=2×100×60.
13.【解答】解:设每箱应降价x元,商场日销售量(100+20x)箱,每箱饮料盈利(12﹣x)元;
依据题意列方程得,
(12﹣x)(100+20x)=1400,
故答案为:(12﹣x)(100+20x)=1400.
14.【解答】解:设每轮传染中1只鸡传染x只鸡,则第一轮传染中有x只鸡被传染,第二种传染中有x(1+x)只鸡被传染,
依题意得:1+x+x(1+x)=81,
整理得:(1+x)2=81,
解得:x1=8,x2=﹣10(不符合题意,舍去),
∴81+81x=81+81×8=729,
∴经过3轮传染后共有729只鸡受到传染.
故答案为:729.
15.【解答】解:设售价为x元,
根据题意得:(x﹣30)[600﹣10(x﹣40)]=10000,
解得:x=50或x=80,
从消费者的角度考虑,
x=80舍去,
答:这种台灯的售价应定为50元.
故答案为:50.
三.解答题(共5小题)
16.【解答】解:(1)小明:设每件皮衣降价x元,则平均每天的销售量为(30+x÷50×10)件,
依题意,得:(1100﹣x﹣750)(30+x÷50×10)=12000;
小红:设每件皮衣定价为y元,则平均每天的销售量为(30+×10)件,
依题意,得:(y﹣750)(30+)=12000.
故答案为:(1100﹣x﹣750)(30+x÷50×10)=12000;(y﹣750)(30+)=12000.
(2)选择小明的设法,则(1100﹣x﹣750)(30+x÷50×10)=12000,
整理,得:x2﹣200x+7500=0,
解得:x1=50,x2=150,
∴1100﹣x=1050或950.
答:每件皮衣定价为1050元或950元.
选择小红的设法,则(y﹣750)(30+)=12000,
整理,得:y2﹣2000y+997500=0,
解得:y1=1050,y2=950.
答:每件皮衣定价为1050元或950元.
17.【解答】解:①设道路的宽为x米.依题意得:
(35﹣2x)(20﹣2x)=600;
②设道路的宽为x米.依题意得:(35﹣x)(20﹣x)=600;
③设道路的宽为x米.依题意得:(35﹣2x)(20﹣x)=540.
18.【解答】解:(1)设其中一条直角边的长为xcm,则另一条直角边的长为(14﹣x)cm,
根据题意得x(14﹣x)=24,
整理得x2﹣14x+48=0.
(2)设十位数字为x,则个位数字为x+3,百位数字为x+2,
根据题意得:9[(x+3)2+x2+(x+2)2]﹣[100(x+2)+10x+(x+3)]=﹣20,
化简得9x2﹣7x﹣22=0.
19.【解答】解:(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),
将(45,550)、(50,500)代入y=kx+b,得:,
解得:,
故年销售量y与销售单价x的函数关系式为y=﹣10x+1000.
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,
根据题意得:(x﹣30)(﹣10x+1000)=12000,
整理,得:x2﹣130x+4200=0,
解得:x1=60,x2=70.
∵此设备的销售单价不得高于65万元,
∴x=60.
答:该设备的销售单价应是60万元/台.
20.【解答】解:当运动时间为ts时,AP=tcm,BP=(5﹣t)cm,BQ=2tcm.
(1)依题意得:(5﹣t)×2t=4,
整理得:t2﹣5t+4=0,
解得:t1=1,t2=4,
当t=1时,2t=2×1=2<7,符合题意;
当t=4时,2t=2×4=8>7,不符合题意,舍去.
答:1s后,△PBQ的面积为4cm2.
(2)依题意得:(5﹣t)2+(2t)2=25,
整理得:t2﹣2t=0,
解得:t1=0(不符合题意,舍去),t2=2.
答:2s后,PQ的长度为5cm
同课章节目录
