2022-2023学年人教版八年级数学上册11.2与三角形有关的角 常考习题检测(含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.2与三角形有关的角 常考习题检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 407.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 14:21:53 | ||
图片预览


文档简介
2022-2023人教版八年级数学上册第十一章
11.2与三角形有关的角 常考习题检测(附带答案)
一.选择题(共10小题)
1.在△ABC中,若∠A=40°,∠B=100°,则∠C=( )
A.70° B.60° C.50° D.40°
2.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠BOC=125°,则∠A的度数为( )
A.70° B.80° C.90° D.55°
3.如图,在△ABC中,∠BCA=40°,∠ABC=60°.若BF是△ABC的高,与角平分线AE相交于点O,则∠EOF的度数为( )
A.130° B.70° C.110 D.100°
4.已知直线l1∥l2,将一块直角三角板ABC(其中∠A是30°,∠C是60°)按如图所示方式放置,若∠1=84°,则∠2等于( )
A.56° B.64° C.66° D.76°
5.如图,直线AB∥CD,如果∠EFB=31°,∠END=70°,那么∠E的度数是( )
A.31° B.40° C.39° D.70°
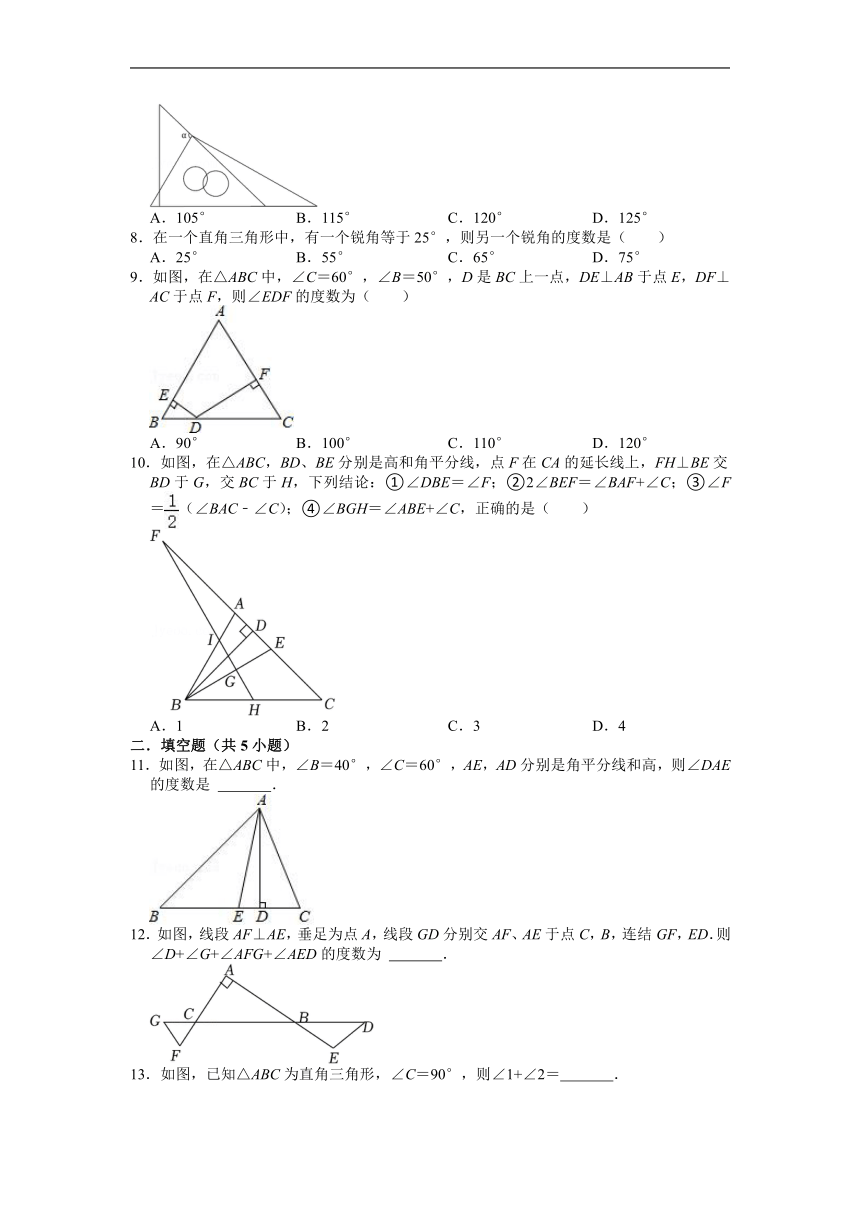
6.如图所示,一副三角板叠放在一起,则图中∠α等于( )
A.105° B.115° C.120° D.135°
7.一副三角板按如图所示方式叠放在一起,则图中∠α等于( )
A.105° B.115° C.120° D.125°
8.在一个直角三角形中,有一个锐角等于25°,则另一个锐角的度数是( )
A.25° B.55° C.65° D.75°
9.如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为( )
A.90° B.100° C.110° D.120°
10.如图,在△ABC,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC﹣∠C);④∠BGH=∠ABE+∠C,正确的是( )
A.1 B.2 C.3 D.4
二.填空题(共5小题)
11.如图,在△ABC中,∠B=40°,∠C=60°,AE,AD分别是角平分线和高,则∠DAE的度数是 .
12.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF、AE于点C,B,连结GF,ED.则∠D+∠G+∠AFG+∠AED的度数为 .
13.如图,已知△ABC为直角三角形,∠C=90°,则∠1+∠2= .
14.如图,∠A=20°,∠B=40°,∠C=50°,则∠ADB的度数是 .
15.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D.若∠A=32°,则∠BCD= °.
三.解答题(共5小题)
16.下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角的和等于180°. 已知:如图,△ABC,求证:∠A+∠B+∠C=180°.
方法一 证明:如图,过点A作DE∥BC. 方法二 证明:如图,过点C作CD∥AB.
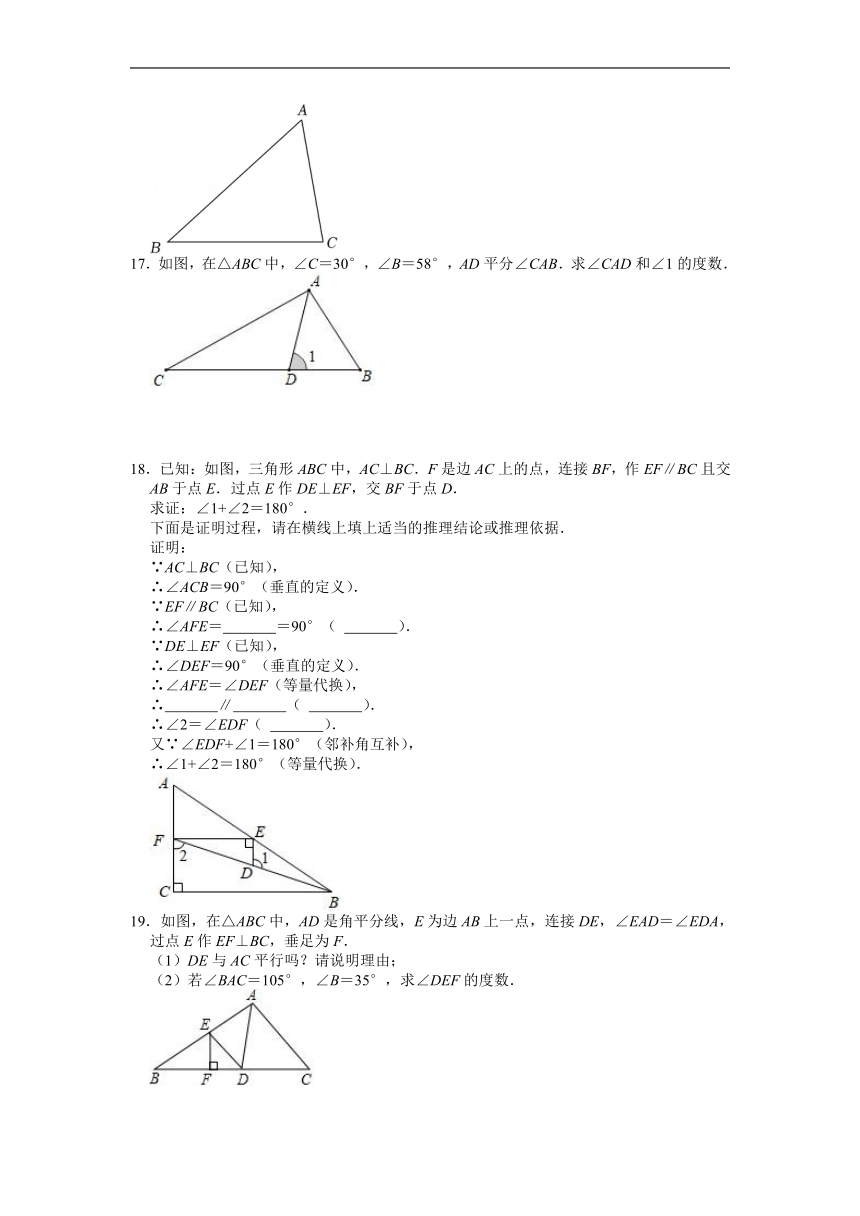
17.如图,在△ABC中,∠C=30°,∠B=58°,AD平分∠CAB.求∠CAD和∠1的度数.
18.已知:如图,三角形ABC中,AC⊥BC.F是边AC上的点,连接BF,作EF∥BC且交AB于点E.过点E作DE⊥EF,交BF于点D.
求证:∠1+∠2=180°.
下面是证明过程,请在横线上填上适当的推理结论或推理依据.
证明:
∵AC⊥BC(已知),
∴∠ACB=90°(垂直的定义).
∵EF∥BC(已知),
∴∠AFE= =90°( ).
∵DE⊥EF(已知),
∴∠DEF=90°(垂直的定义).
∴∠AFE=∠DEF(等量代换),
∴ ∥ ( ).
∴∠2=∠EDF( ).
又∵∠EDF+∠1=180°(邻补角互补),
∴∠1+∠2=180°(等量代换).
19.如图,在△ABC中,AD是角平分线,E为边AB上一点,连接DE,∠EAD=∠EDA,过点E作EF⊥BC,垂足为F.
(1)DE与AC平行吗?请说明理由;
(2)若∠BAC=105°,∠B=35°,求∠DEF的度数.
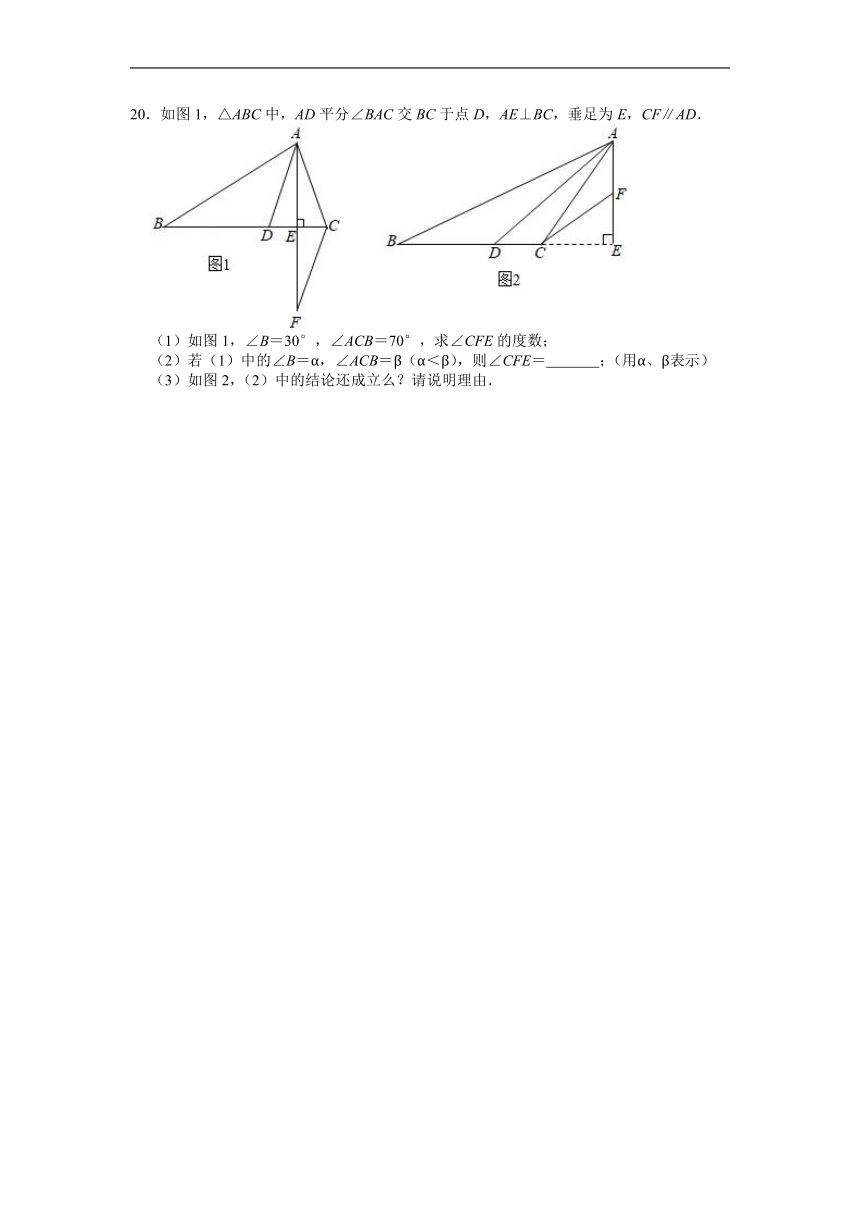
20.如图1,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,CF∥AD.
(1)如图1,∠B=30°,∠ACB=70°,求∠CFE的度数;
(2)若(1)中的∠B=α,∠ACB=β(α<β),则∠CFE= ;(用α、β表示)
(3)如图2,(2)中的结论还成立么?请说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:在△ABC中,∵∠A=40°,∠B=100°,
∴∠C=180°﹣∠A﹣∠B=40°,
故选:D.
2.【解答】解:∵BO平分∠ABC,CO平分∠ACB,
∴设∠ABO=∠CBO=α,∠ACO=∠BCO=β,
则有:
α+β+∠O=180°,2α+2β+∠A=180°,
∴α+β=180°﹣∠O且α+β=,
∴180°﹣∠O=,
解得:∠A=70°,
故选:A.
3.【解答】解:∵∠BCA=40°,∠ABC=60°,
∴∠BAC=180°﹣∠BCA﹣∠ABC
=180°﹣40°﹣60°
=80°.
∵AE是∠BAC的平分线,
∴∠EAC=∠BAC=40°.
∵BF是△ABC的高,
∴∠BFA=90°.
∴∠AOF=90°﹣∠EAC
=90°﹣40°
=50°.
∴∠EOF=180°﹣∠AOF
=180°﹣50°
=130°.
故选:A.
4.【解答】解:∵∠3+∠4+∠A=180°,∠A=30°,∠4=∠1=84°,
∴∠3=180°﹣∠A﹣∠4=180°﹣30°﹣84°=66°.
又∵直线l1∥l2,
∴∠2=∠3=66°.
故选:C.
5.【解答】解:∵直线AB∥CD,
∴∠EMB=∠END=70°,
∵∠EFB=31°,∠EMB=∠E+∠EFB,
∴∠E=70°﹣31°=39°,
故选:C.
6.【解答】解:如图,
由题意得:∠ABG=90°,
∵∠G=30°,
∴∠BFG=180°﹣∠ABG﹣∠G=60°,
∴∠AFH=∠BFG=60°,
∵∠α是△AFH的外角,∠A=45°,
∴∠α=∠A+∠AFH=105°,
故选:A.
7.【解答】解:如图,
∵∠α是△BDC的外角,∠D=60°,∠BCD=45°,
∴∠α=∠D+∠BCD=60°+45°=105°,
故选:A.
8.【解答】解:∵在一个直角三角形中,有一个锐角等于25°,
∴另一个锐角的度数是90°﹣25°=65°.
故选:C.
9.【解答】解:如图,∵在△ABC中,∠C=60°,∠B=50°,
∴∠A=70°.
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°,
∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°.
故选:C.
10.【解答】解:设BD交FH于点J.
①∵BD⊥FD,
∴∠FJD+∠F=90°
∵FH⊥BE,
∴∠BJG+∠DBE=90°,
∵∠FJD=∠BJG,
∴∠DBE=∠F,
①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
②正确;
③∠ABD=90°﹣∠BAC,
∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,
∵∠CBD=90°﹣∠C,
∴∠DBE=∠BAC﹣∠C﹣∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC﹣∠C﹣∠DBE,
∴∠F=(∠BAC﹣∠C);
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故选:D.
二.填空题(共5小题)
11.【解答】解:∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AE是△ABC的角平分线,
∴∠BAE=∠EAC=∠BAC=40°,
又∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°﹣∠B﹣∠ADB=50°,
∴∠DAE=∠BAD﹣∠BAE=50°﹣40°=10°.
故答案为:10°.
12.【解答】解:∵∠A+∠ACB+∠ABC=180°,∠A=90°,
∴∠ACB+∠ABC=90°,
∵∠GCF=∠ACB,∠DBE=∠ABC,
∴∠GCF+∠DBE=90°,
∵∠G+∠F+∠GCF=∠D+∠B+∠DBE=180°,
∴∠G+∠F+∠GCF+∠D+∠B+∠DBE=360°,
∴∠D+∠G+∠AFG+∠AED=270°,
故答案为:270°.
13.【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°,
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
故答案为:270°.
14.【解答】解:∵∠A=20°,∠C=50°,
∴∠AEB=∠A+∠C=70°,
∵∠B=40°,
∴∠ADB=∠AEB+∠B=70°+40°=110°,
故答案为:110°.
15.【解答】解:∵∠C=90°,
∴∠BCD+∠ACD=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD=∠A=32°,
故答案为:32.
三.解答题(共5小题)
16.【解答】证明:方法一:∵DE∥BC,
∴∠B=∠BAD,∠C=∠CAE,
∵∠BAD+∠BAC+∠CAE=180°,
∴∠B+∠BAC+∠C=180°;
方法二:∵CD∥AB,
∴∠A=∠ACD,∠B+∠BCD=180°,
∴∠B+∠ACB+∠A=180°.
17.【解答】解:∵∠C=30°,∠B=58°,
∴∠CAB=180°﹣30°﹣58°=92°,
∵AD平分∠CAB,
∴∠CAD=∠CAB=46°;
∵∠CAD=46°,∠C=30°,
∴∠1=∠CAD+∠C=46°+30°=76°.
18.【解答】证明:∵AC⊥BC(已知),
∴∠ACB=90°(垂线的定义).
∵EF∥BC(已知),
∴∠AFE=∠ACB=90°(两直线平行,同位角相等).
∵DE⊥EF(已知),
∴∠DEF=90°(垂线的定义).
∴∠AFE=∠DEF(等量代换).
∴DE∥AC(内错角相等,两直线平行).
∴∠2=∠EDF(两直线平行,内错角相等).
∵∠EDF+∠1=180°(邻补角互补),
∴∠1+∠2=180°(等量代换).
故答案为:∠ACB;两直线平行,同位角相等;DE;AC;内错角相等,两直线平行;两直线平行,内错角相等,
19.【解答】解:(1)DE∥AC.
理由如下:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠EAD=∠EDA,
∴∠CAD=∠EDA,
∴DE∥AC;
(2)∵∠B+∠C+∠BAC=180°,
∴∠C=180°﹣105°﹣35°=40°,
∵DE∥AC,
∴∠EDF=∠C=40°,
∵EF⊥BD,
∴∠EFD=90°,
∴∠DEF=90°﹣∠EDF=90°﹣40°=50°.
20.【解答】解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,∠B=α,∠ACB=β,
∴∠CFE=∠DAE=20°;
(2)∵∠BAE=90°﹣∠B,∠BAD=∠BAC=(180°﹣∠B﹣∠ACB),
∵CF∥AD,
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣(180°﹣∠B﹣∠BCA)=(∠ACB﹣∠B)=β﹣α,
故答案为:β﹣α;
(3)(2)中的结论成立.
∵∠B=α,∠ACB=β,
∴∠BAC=180°﹣α﹣β,
∵AD平分∠BAC,
∴∠DAC=∠BAC=90°﹣α﹣β,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣α﹣β,
∴∠BCF=β+90°﹣α﹣β=90°﹣α+β,
∴∠ECF=180°﹣∠BCF=90°+α﹣β,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=β﹣α;
11.2与三角形有关的角 常考习题检测(附带答案)
一.选择题(共10小题)
1.在△ABC中,若∠A=40°,∠B=100°,则∠C=( )
A.70° B.60° C.50° D.40°
2.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠BOC=125°,则∠A的度数为( )
A.70° B.80° C.90° D.55°
3.如图,在△ABC中,∠BCA=40°,∠ABC=60°.若BF是△ABC的高,与角平分线AE相交于点O,则∠EOF的度数为( )
A.130° B.70° C.110 D.100°
4.已知直线l1∥l2,将一块直角三角板ABC(其中∠A是30°,∠C是60°)按如图所示方式放置,若∠1=84°,则∠2等于( )
A.56° B.64° C.66° D.76°
5.如图,直线AB∥CD,如果∠EFB=31°,∠END=70°,那么∠E的度数是( )
A.31° B.40° C.39° D.70°
6.如图所示,一副三角板叠放在一起,则图中∠α等于( )
A.105° B.115° C.120° D.135°
7.一副三角板按如图所示方式叠放在一起,则图中∠α等于( )
A.105° B.115° C.120° D.125°
8.在一个直角三角形中,有一个锐角等于25°,则另一个锐角的度数是( )
A.25° B.55° C.65° D.75°
9.如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为( )
A.90° B.100° C.110° D.120°
10.如图,在△ABC,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC﹣∠C);④∠BGH=∠ABE+∠C,正确的是( )
A.1 B.2 C.3 D.4
二.填空题(共5小题)
11.如图,在△ABC中,∠B=40°,∠C=60°,AE,AD分别是角平分线和高,则∠DAE的度数是 .
12.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF、AE于点C,B,连结GF,ED.则∠D+∠G+∠AFG+∠AED的度数为 .
13.如图,已知△ABC为直角三角形,∠C=90°,则∠1+∠2= .
14.如图,∠A=20°,∠B=40°,∠C=50°,则∠ADB的度数是 .
15.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D.若∠A=32°,则∠BCD= °.
三.解答题(共5小题)
16.下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角的和等于180°. 已知:如图,△ABC,求证:∠A+∠B+∠C=180°.
方法一 证明:如图,过点A作DE∥BC. 方法二 证明:如图,过点C作CD∥AB.
17.如图,在△ABC中,∠C=30°,∠B=58°,AD平分∠CAB.求∠CAD和∠1的度数.
18.已知:如图,三角形ABC中,AC⊥BC.F是边AC上的点,连接BF,作EF∥BC且交AB于点E.过点E作DE⊥EF,交BF于点D.
求证:∠1+∠2=180°.
下面是证明过程,请在横线上填上适当的推理结论或推理依据.
证明:
∵AC⊥BC(已知),
∴∠ACB=90°(垂直的定义).
∵EF∥BC(已知),
∴∠AFE= =90°( ).
∵DE⊥EF(已知),
∴∠DEF=90°(垂直的定义).
∴∠AFE=∠DEF(等量代换),
∴ ∥ ( ).
∴∠2=∠EDF( ).
又∵∠EDF+∠1=180°(邻补角互补),
∴∠1+∠2=180°(等量代换).
19.如图,在△ABC中,AD是角平分线,E为边AB上一点,连接DE,∠EAD=∠EDA,过点E作EF⊥BC,垂足为F.
(1)DE与AC平行吗?请说明理由;
(2)若∠BAC=105°,∠B=35°,求∠DEF的度数.
20.如图1,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,CF∥AD.
(1)如图1,∠B=30°,∠ACB=70°,求∠CFE的度数;
(2)若(1)中的∠B=α,∠ACB=β(α<β),则∠CFE= ;(用α、β表示)
(3)如图2,(2)中的结论还成立么?请说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:在△ABC中,∵∠A=40°,∠B=100°,
∴∠C=180°﹣∠A﹣∠B=40°,
故选:D.
2.【解答】解:∵BO平分∠ABC,CO平分∠ACB,
∴设∠ABO=∠CBO=α,∠ACO=∠BCO=β,
则有:
α+β+∠O=180°,2α+2β+∠A=180°,
∴α+β=180°﹣∠O且α+β=,
∴180°﹣∠O=,
解得:∠A=70°,
故选:A.
3.【解答】解:∵∠BCA=40°,∠ABC=60°,
∴∠BAC=180°﹣∠BCA﹣∠ABC
=180°﹣40°﹣60°
=80°.
∵AE是∠BAC的平分线,
∴∠EAC=∠BAC=40°.
∵BF是△ABC的高,
∴∠BFA=90°.
∴∠AOF=90°﹣∠EAC
=90°﹣40°
=50°.
∴∠EOF=180°﹣∠AOF
=180°﹣50°
=130°.
故选:A.
4.【解答】解:∵∠3+∠4+∠A=180°,∠A=30°,∠4=∠1=84°,
∴∠3=180°﹣∠A﹣∠4=180°﹣30°﹣84°=66°.
又∵直线l1∥l2,
∴∠2=∠3=66°.
故选:C.
5.【解答】解:∵直线AB∥CD,
∴∠EMB=∠END=70°,
∵∠EFB=31°,∠EMB=∠E+∠EFB,
∴∠E=70°﹣31°=39°,
故选:C.
6.【解答】解:如图,
由题意得:∠ABG=90°,
∵∠G=30°,
∴∠BFG=180°﹣∠ABG﹣∠G=60°,
∴∠AFH=∠BFG=60°,
∵∠α是△AFH的外角,∠A=45°,
∴∠α=∠A+∠AFH=105°,
故选:A.
7.【解答】解:如图,
∵∠α是△BDC的外角,∠D=60°,∠BCD=45°,
∴∠α=∠D+∠BCD=60°+45°=105°,
故选:A.
8.【解答】解:∵在一个直角三角形中,有一个锐角等于25°,
∴另一个锐角的度数是90°﹣25°=65°.
故选:C.
9.【解答】解:如图,∵在△ABC中,∠C=60°,∠B=50°,
∴∠A=70°.
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°,
∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°.
故选:C.
10.【解答】解:设BD交FH于点J.
①∵BD⊥FD,
∴∠FJD+∠F=90°
∵FH⊥BE,
∴∠BJG+∠DBE=90°,
∵∠FJD=∠BJG,
∴∠DBE=∠F,
①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
②正确;
③∠ABD=90°﹣∠BAC,
∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,
∵∠CBD=90°﹣∠C,
∴∠DBE=∠BAC﹣∠C﹣∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC﹣∠C﹣∠DBE,
∴∠F=(∠BAC﹣∠C);
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故选:D.
二.填空题(共5小题)
11.【解答】解:∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AE是△ABC的角平分线,
∴∠BAE=∠EAC=∠BAC=40°,
又∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°﹣∠B﹣∠ADB=50°,
∴∠DAE=∠BAD﹣∠BAE=50°﹣40°=10°.
故答案为:10°.
12.【解答】解:∵∠A+∠ACB+∠ABC=180°,∠A=90°,
∴∠ACB+∠ABC=90°,
∵∠GCF=∠ACB,∠DBE=∠ABC,
∴∠GCF+∠DBE=90°,
∵∠G+∠F+∠GCF=∠D+∠B+∠DBE=180°,
∴∠G+∠F+∠GCF+∠D+∠B+∠DBE=360°,
∴∠D+∠G+∠AFG+∠AED=270°,
故答案为:270°.
13.【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°,
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
故答案为:270°.
14.【解答】解:∵∠A=20°,∠C=50°,
∴∠AEB=∠A+∠C=70°,
∵∠B=40°,
∴∠ADB=∠AEB+∠B=70°+40°=110°,
故答案为:110°.
15.【解答】解:∵∠C=90°,
∴∠BCD+∠ACD=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD=∠A=32°,
故答案为:32.
三.解答题(共5小题)
16.【解答】证明:方法一:∵DE∥BC,
∴∠B=∠BAD,∠C=∠CAE,
∵∠BAD+∠BAC+∠CAE=180°,
∴∠B+∠BAC+∠C=180°;
方法二:∵CD∥AB,
∴∠A=∠ACD,∠B+∠BCD=180°,
∴∠B+∠ACB+∠A=180°.
17.【解答】解:∵∠C=30°,∠B=58°,
∴∠CAB=180°﹣30°﹣58°=92°,
∵AD平分∠CAB,
∴∠CAD=∠CAB=46°;
∵∠CAD=46°,∠C=30°,
∴∠1=∠CAD+∠C=46°+30°=76°.
18.【解答】证明:∵AC⊥BC(已知),
∴∠ACB=90°(垂线的定义).
∵EF∥BC(已知),
∴∠AFE=∠ACB=90°(两直线平行,同位角相等).
∵DE⊥EF(已知),
∴∠DEF=90°(垂线的定义).
∴∠AFE=∠DEF(等量代换).
∴DE∥AC(内错角相等,两直线平行).
∴∠2=∠EDF(两直线平行,内错角相等).
∵∠EDF+∠1=180°(邻补角互补),
∴∠1+∠2=180°(等量代换).
故答案为:∠ACB;两直线平行,同位角相等;DE;AC;内错角相等,两直线平行;两直线平行,内错角相等,
19.【解答】解:(1)DE∥AC.
理由如下:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠EAD=∠EDA,
∴∠CAD=∠EDA,
∴DE∥AC;
(2)∵∠B+∠C+∠BAC=180°,
∴∠C=180°﹣105°﹣35°=40°,
∵DE∥AC,
∴∠EDF=∠C=40°,
∵EF⊥BD,
∴∠EFD=90°,
∴∠DEF=90°﹣∠EDF=90°﹣40°=50°.
20.【解答】解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,∠B=α,∠ACB=β,
∴∠CFE=∠DAE=20°;
(2)∵∠BAE=90°﹣∠B,∠BAD=∠BAC=(180°﹣∠B﹣∠ACB),
∵CF∥AD,
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣(180°﹣∠B﹣∠BCA)=(∠ACB﹣∠B)=β﹣α,
故答案为:β﹣α;
(3)(2)中的结论成立.
∵∠B=α,∠ACB=β,
∴∠BAC=180°﹣α﹣β,
∵AD平分∠BAC,
∴∠DAC=∠BAC=90°﹣α﹣β,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣α﹣β,
∴∠BCF=β+90°﹣α﹣β=90°﹣α+β,
∴∠ECF=180°﹣∠BCF=90°+α﹣β,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=β﹣α;
