2022-2023学年人教版八年级数学上册11.1与三角形有关的线段 常考习题检测 (含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.1与三角形有关的线段 常考习题检测 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 335.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 14:22:40 | ||
图片预览




文档简介
2022-2023人教版八年级数学上册第十一章
11.1与三角形有关的线段 常考习题检测(附带答案)
一.选择题(共10小题)
1.如图中三角形的个数是( )
A.6 B.7 C.8 D.9
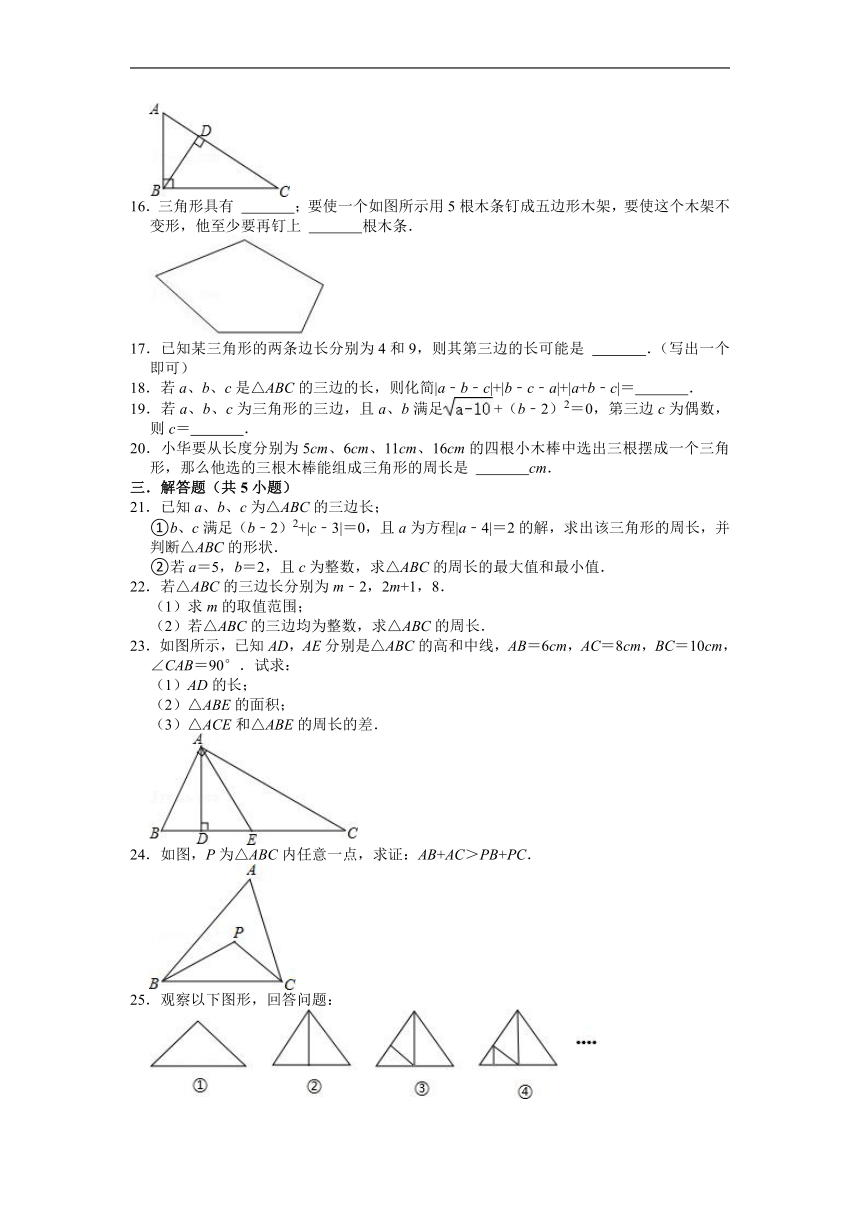
2.下列四个图形中,线段BE是△ABC的高的是( )
A. B.
C. D.
3.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
4.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm B.4cm C.6cm D.18cm
5.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
6.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短 B.垂线段最短
C.两直线平行,内错角相等 D.三角形具有稳定性
7.下列长度的三条线段能组成三角形的是( )
A.3cm,5cm,7cm B.3cm,3cm,7cm
C.4cm,4cm,8cm D.4cm,5cm,9cm
8.某木材市场上木棒规格与对应价格如下表:
规格 1m 2m 3m 4m 5m 6m
价格(元/根) 10 15 20 25 30 35
小明的爷爷要做一个三角形木架养鱼用,现有两根长度分别为3m和5m的木棒,还需要到该木材市场购买一根木棒.则小明的爷爷至少带的钱数应为( )
A.10 B.15 C.20 D.25
9.袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
10.一个三角形的3边长分别是xcm、(3x﹣3)cm、(x+2)cm,它的周长不超过39cm.则x的取值范围是( )
A.<x<5 B.5<x≤8 C.<x≤8 D.1<x<5
二.填空题(共10小题)
11.在△ABC中,三边长的比是3:4:5,其周长为48cm,那么它的三边长为 .
12.用一副三角板拼成的图形如图所示,其中B,C,D三点在同一条直线上,则∠ACE= .
13.如图,CM是△ABC的中线,AB=10,则BM的长为 .
14.已知AD是△ABC的中线,点D在BC上,△ABD的周长比△ACD的周长多2,AB与AC的和为12,则AB的长为 .
15.如图,直角三角形ABC中,∠ABC=90°,BD⊥AC于点D,AB=3,AD=1.8,BD=2.4,DC=3.2,BC=4,则点A到BD的距离是 .
16.三角形具有 ;要使一个如图所示用5根木条钉成五边形木架,要使这个木架不变形,他至少要再钉上 根木条.
17.已知某三角形的两条边长分别为4和9,则其第三边的长可能是 .(写出一个即可)
18.若a、b、c是△ABC的三边的长,则化简|a﹣b﹣c|+|b﹣c﹣a|+|a+b﹣c|= .
19.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为偶数,则c= .
20.小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒能组成三角形的周长是 cm.
三.解答题(共5小题)
21.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
22.若△ABC的三边长分别为m﹣2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
23.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
24.如图,P为△ABC内任意一点,求证:AB+AC>PB+PC.
25.观察以下图形,回答问题:
(1)图②有 个三角形;图③有 个三角形;图④有 个三角形;…猜测第七个图形中共有 个三角形.
(2)按上面的方法继续下去,第n个图形中有 个三角形(用含n的代数式表示结论).
参考答案与试题解析
一.选择题(共10小题)
1.如图中三角形的个数是( )
A.6 B.7 C.8 D.9
【解答】解:∵图中三角形有:△ECA,△EBD,△FBA,△FCD,△AFD,△ABD,△ACD,△AED,
∴共8个.
故选:C.
2.下列四个图形中,线段BE是△ABC的高的是( )
A. B.
C. D.
【解答】解:线段BE是△ABC的高的图是选项C.
故选:C.
3.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
【解答】解:∵CM为△ABC的AB边上的中线,
∴AM=BM,
∵△BCM的周长比△ACM的周长大3cm,
∴(BC+BM+CM)﹣(AC+AM+CM)=3cm,
∴BC﹣AC=3cm,
∵BC=8cm,
∴AC=5cm,
故选:C.
4.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm B.4cm C.6cm D.18cm
【解答】解:∵AD为中线,
∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC,
∵AB=10,AC=8,
∴△ABD与△ACD的周长之差=10﹣8=2(cm).
故选:A.
5.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
【解答】解:△ABC的BC边上的高是AF,
故选:B.
6.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短 B.垂线段最短
C.两直线平行,内错角相等 D.三角形具有稳定性
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
7.下列长度的三条线段能组成三角形的是( )
A.3cm,5cm,7cm B.3cm,3cm,7cm
C.4cm,4cm,8cm D.4cm,5cm,9cm
【解答】解:A.∵3+5=8>7,
∴能组成三角形,符合题意;
B.∵3+3<7,
∴不能组成三角形,不符合题意;
C.∵4+4=8,
∴不能组成三角形,不符合题意;
D.∵4+5=9,
∴不能组成三角形,不符合题意.
故选:A.
8.某木材市场上木棒规格与对应价格如下表:
规格 1m 2m 3m 4m 5m 6m
价格(元/根) 10 15 20 25 30 35
小明的爷爷要做一个三角形木架养鱼用,现有两根长度分别为3m和5m的木棒,还需要到该木材市场购买一根木棒.则小明的爷爷至少带的钱数应为( )
A.10 B.15 C.20 D.25
【解答】解:设第三根木棒的长度为xm,
根据三角形的三边关系可得:5﹣3<x<5+3,
解得2<x<8,
x=3,4,5,6,7,共5种选择,
根据木棒的价格可得选3m最省钱,
所以小明的爷爷至少带的钱数应为20元,
故选:C.
9.袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
【解答】解:设第三根木棒的长为xcm,
∵已经取了10cm和15cm两根木棍,
∴15﹣10<x<15+10,即5<x<25.
∴四个选项中只有D不在其范围内,符合题意.
故选:D.
10.一个三角形的3边长分别是xcm、(3x﹣3)cm、(x+2)cm,它的周长不超过39cm.则x的取值范围是( )
A.<x<5 B.5<x≤8 C.<x≤8 D.1<x<5
【解答】解:由题意得:x+3x﹣3+x+2≤39,
解得:x≤8,
由三角形的三边关系可知:x+3x﹣3>x+2,x+x+2>3x﹣3,
解得:x>,x<5,
∴<x≤5,
故选:A.
二.填空题(共10小题)
11.在△ABC中,三边长的比是3:4:5,其周长为48cm,那么它的三边长为 12cm,16cm,20cm .
【解答】解:设△ABC的三边长分别为3xcm、4xcm、5xcm,
由题意得:3x+4x+5x=48,
解得:x=4,
∴3x=12cm,4x=16cm,5x=20cm;
故答案为:12cm,16cm,20cm.
12.用一副三角板拼成的图形如图所示,其中B,C,D三点在同一条直线上,则∠ACE= 75° .
【解答】解:∠ACE=180°﹣∠ACB﹣∠ECD=180°﹣60°﹣45°=75°,
故答案为:75°.
13.如图,CM是△ABC的中线,AB=10,则BM的长为 5 .
【解答】解:∵CM是△ABC的中线,
∴AM=BM=AB,
∵AB=10,
∴BM=×10=5,
故答案为:5.
14.已知AD是△ABC的中线,点D在BC上,△ABD的周长比△ACD的周长多2,AB与AC的和为12,则AB的长为 7 .
【解答】解:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD的周长多2,
∴(AB+BD+AD)﹣(AC+CD+AD)=AB﹣AC=2,
则,
解得:,
故答案为:7.
15.如图,直角三角形ABC中,∠ABC=90°,BD⊥AC于点D,AB=3,AD=1.8,BD=2.4,DC=3.2,BC=4,则点A到BD的距离是 1.8 .
【解答】解:∵BD⊥AC,AD=1.8,
∴点A到BD的距离为1.8,
故答案为:1.8.
16.三角形具有 稳定性 ;要使一个如图所示用5根木条钉成五边形木架,要使这个木架不变形,他至少要再钉上 2 根木条.
【解答】解:∵三角形具有稳定性,
∴要使这个木架不变形,至少要再钉上如图中虚线所示的2根木条,
故答案为:稳定性;2.
17.已知某三角形的两条边长分别为4和9,则其第三边的长可能是 8(答案不唯一) .(写出一个即可)
【解答】解:设第三边的长为x,
则9﹣4<x<9+4,即5<x<13,
∴第三边的长可能是8,
故答案为:8(答案不唯一).
18.若a、b、c是△ABC的三边的长,则化简|a﹣b﹣c|+|b﹣c﹣a|+|a+b﹣c|= a+b+c .
【解答】解:∵a、b、c是△ABC的三边长,
∴a<b+c,b<a+c,c<a+b,
∴|a﹣b﹣c|+|b﹣c﹣a|+|a+b﹣c|=b+c﹣a+c+a﹣b+a+b﹣c=a+b+c;
故答案是:a+b+c.
19.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为偶数,则c= 10 .
【解答】解:∵a、b满足+(b﹣2)2=0,
∴a=10,b=2,
∵a、b、c为三角形的三边,
∴8<c<12,
∵第三边c为偶数,
∴c=10.
故答案为:10.
20.小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒能组成三角形的周长是 33 cm.
【解答】解:四根小木棒选出三根的情况有:5cm,6cm,11cm;5cm,6cm,16cm;5cm,11cm,16cm;6cm,11cm,16cm,共4种情况,
∵5+6=11,5+6<16,5+11=16,
∴构成三角形的情况有:6cm,11cm,16cm,1种情况,
此时三根木棒形成的三角形的周长=6+11+16=33(cm),
故答案为:33.
三.解答题(共5小题)
21.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
【解答】解:①∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|a﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴a=2,
∴△ABC的周长为:2+2+3=7,
∴△ABC是等腰三角形.
②∵a=5,b=2,c为整数,
∴5﹣2<c<2+5,
∴c的最小值为4,c的最大值为6,
∴△ABC的周长的最大值=5+2+6=13,最小值=5+2+4=11.
22.若△ABC的三边长分别为m﹣2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
【解答】解:(1)根据三角形的三边关系,
,
解得:3<m<5;
(2)因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m﹣2)+(2m+1)+8=3m+7=3×4+7=19.
23.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
【解答】解:∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD===4.8(cm),即AD的长度为4.8cm;
(2)方法一:如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
方法二:因为BE=BC=5,由(1)知AD=4.8,
所以S△ABE=BE AD=×5×4.8=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE)=AC﹣AB=8﹣6=2(cm),即△ACE和△ABE的周长的差是2cm.
24.如图,P为△ABC内任意一点,求证:AB+AC>PB+PC.
【解答】证明:延长BP交AC于点D,
在△ABD中,PB+PD<AB+AD①
在△PCD中,PC<PD+CD②
①+②得PB+PD+PC<AB+AD+PD+CD,
即PB+PC<AB+AC,
即:AB+AC>PB+PC.
25.观察以下图形,回答问题:
(1)图②有 3 个三角形;图③有 5 个三角形;图④有 7 个三角形;…猜测第七个图形中共有 13 个三角形.
(2)按上面的方法继续下去,第n个图形中有 (2n﹣1) 个三角形(用含n的代数式表示结论).
【解答】解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
11.1与三角形有关的线段 常考习题检测(附带答案)
一.选择题(共10小题)
1.如图中三角形的个数是( )
A.6 B.7 C.8 D.9
2.下列四个图形中,线段BE是△ABC的高的是( )
A. B.
C. D.
3.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
4.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm B.4cm C.6cm D.18cm
5.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
6.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短 B.垂线段最短
C.两直线平行,内错角相等 D.三角形具有稳定性
7.下列长度的三条线段能组成三角形的是( )
A.3cm,5cm,7cm B.3cm,3cm,7cm
C.4cm,4cm,8cm D.4cm,5cm,9cm
8.某木材市场上木棒规格与对应价格如下表:
规格 1m 2m 3m 4m 5m 6m
价格(元/根) 10 15 20 25 30 35
小明的爷爷要做一个三角形木架养鱼用,现有两根长度分别为3m和5m的木棒,还需要到该木材市场购买一根木棒.则小明的爷爷至少带的钱数应为( )
A.10 B.15 C.20 D.25
9.袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
10.一个三角形的3边长分别是xcm、(3x﹣3)cm、(x+2)cm,它的周长不超过39cm.则x的取值范围是( )
A.<x<5 B.5<x≤8 C.<x≤8 D.1<x<5
二.填空题(共10小题)
11.在△ABC中,三边长的比是3:4:5,其周长为48cm,那么它的三边长为 .
12.用一副三角板拼成的图形如图所示,其中B,C,D三点在同一条直线上,则∠ACE= .
13.如图,CM是△ABC的中线,AB=10,则BM的长为 .
14.已知AD是△ABC的中线,点D在BC上,△ABD的周长比△ACD的周长多2,AB与AC的和为12,则AB的长为 .
15.如图,直角三角形ABC中,∠ABC=90°,BD⊥AC于点D,AB=3,AD=1.8,BD=2.4,DC=3.2,BC=4,则点A到BD的距离是 .
16.三角形具有 ;要使一个如图所示用5根木条钉成五边形木架,要使这个木架不变形,他至少要再钉上 根木条.
17.已知某三角形的两条边长分别为4和9,则其第三边的长可能是 .(写出一个即可)
18.若a、b、c是△ABC的三边的长,则化简|a﹣b﹣c|+|b﹣c﹣a|+|a+b﹣c|= .
19.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为偶数,则c= .
20.小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒能组成三角形的周长是 cm.
三.解答题(共5小题)
21.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
22.若△ABC的三边长分别为m﹣2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
23.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
24.如图,P为△ABC内任意一点,求证:AB+AC>PB+PC.
25.观察以下图形,回答问题:
(1)图②有 个三角形;图③有 个三角形;图④有 个三角形;…猜测第七个图形中共有 个三角形.
(2)按上面的方法继续下去,第n个图形中有 个三角形(用含n的代数式表示结论).
参考答案与试题解析
一.选择题(共10小题)
1.如图中三角形的个数是( )
A.6 B.7 C.8 D.9
【解答】解:∵图中三角形有:△ECA,△EBD,△FBA,△FCD,△AFD,△ABD,△ACD,△AED,
∴共8个.
故选:C.
2.下列四个图形中,线段BE是△ABC的高的是( )
A. B.
C. D.
【解答】解:线段BE是△ABC的高的图是选项C.
故选:C.
3.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
【解答】解:∵CM为△ABC的AB边上的中线,
∴AM=BM,
∵△BCM的周长比△ACM的周长大3cm,
∴(BC+BM+CM)﹣(AC+AM+CM)=3cm,
∴BC﹣AC=3cm,
∵BC=8cm,
∴AC=5cm,
故选:C.
4.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm B.4cm C.6cm D.18cm
【解答】解:∵AD为中线,
∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC,
∵AB=10,AC=8,
∴△ABD与△ACD的周长之差=10﹣8=2(cm).
故选:A.
5.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
【解答】解:△ABC的BC边上的高是AF,
故选:B.
6.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短 B.垂线段最短
C.两直线平行,内错角相等 D.三角形具有稳定性
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
7.下列长度的三条线段能组成三角形的是( )
A.3cm,5cm,7cm B.3cm,3cm,7cm
C.4cm,4cm,8cm D.4cm,5cm,9cm
【解答】解:A.∵3+5=8>7,
∴能组成三角形,符合题意;
B.∵3+3<7,
∴不能组成三角形,不符合题意;
C.∵4+4=8,
∴不能组成三角形,不符合题意;
D.∵4+5=9,
∴不能组成三角形,不符合题意.
故选:A.
8.某木材市场上木棒规格与对应价格如下表:
规格 1m 2m 3m 4m 5m 6m
价格(元/根) 10 15 20 25 30 35
小明的爷爷要做一个三角形木架养鱼用,现有两根长度分别为3m和5m的木棒,还需要到该木材市场购买一根木棒.则小明的爷爷至少带的钱数应为( )
A.10 B.15 C.20 D.25
【解答】解:设第三根木棒的长度为xm,
根据三角形的三边关系可得:5﹣3<x<5+3,
解得2<x<8,
x=3,4,5,6,7,共5种选择,
根据木棒的价格可得选3m最省钱,
所以小明的爷爷至少带的钱数应为20元,
故选:C.
9.袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
【解答】解:设第三根木棒的长为xcm,
∵已经取了10cm和15cm两根木棍,
∴15﹣10<x<15+10,即5<x<25.
∴四个选项中只有D不在其范围内,符合题意.
故选:D.
10.一个三角形的3边长分别是xcm、(3x﹣3)cm、(x+2)cm,它的周长不超过39cm.则x的取值范围是( )
A.<x<5 B.5<x≤8 C.<x≤8 D.1<x<5
【解答】解:由题意得:x+3x﹣3+x+2≤39,
解得:x≤8,
由三角形的三边关系可知:x+3x﹣3>x+2,x+x+2>3x﹣3,
解得:x>,x<5,
∴<x≤5,
故选:A.
二.填空题(共10小题)
11.在△ABC中,三边长的比是3:4:5,其周长为48cm,那么它的三边长为 12cm,16cm,20cm .
【解答】解:设△ABC的三边长分别为3xcm、4xcm、5xcm,
由题意得:3x+4x+5x=48,
解得:x=4,
∴3x=12cm,4x=16cm,5x=20cm;
故答案为:12cm,16cm,20cm.
12.用一副三角板拼成的图形如图所示,其中B,C,D三点在同一条直线上,则∠ACE= 75° .
【解答】解:∠ACE=180°﹣∠ACB﹣∠ECD=180°﹣60°﹣45°=75°,
故答案为:75°.
13.如图,CM是△ABC的中线,AB=10,则BM的长为 5 .
【解答】解:∵CM是△ABC的中线,
∴AM=BM=AB,
∵AB=10,
∴BM=×10=5,
故答案为:5.
14.已知AD是△ABC的中线,点D在BC上,△ABD的周长比△ACD的周长多2,AB与AC的和为12,则AB的长为 7 .
【解答】解:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD的周长多2,
∴(AB+BD+AD)﹣(AC+CD+AD)=AB﹣AC=2,
则,
解得:,
故答案为:7.
15.如图,直角三角形ABC中,∠ABC=90°,BD⊥AC于点D,AB=3,AD=1.8,BD=2.4,DC=3.2,BC=4,则点A到BD的距离是 1.8 .
【解答】解:∵BD⊥AC,AD=1.8,
∴点A到BD的距离为1.8,
故答案为:1.8.
16.三角形具有 稳定性 ;要使一个如图所示用5根木条钉成五边形木架,要使这个木架不变形,他至少要再钉上 2 根木条.
【解答】解:∵三角形具有稳定性,
∴要使这个木架不变形,至少要再钉上如图中虚线所示的2根木条,
故答案为:稳定性;2.
17.已知某三角形的两条边长分别为4和9,则其第三边的长可能是 8(答案不唯一) .(写出一个即可)
【解答】解:设第三边的长为x,
则9﹣4<x<9+4,即5<x<13,
∴第三边的长可能是8,
故答案为:8(答案不唯一).
18.若a、b、c是△ABC的三边的长,则化简|a﹣b﹣c|+|b﹣c﹣a|+|a+b﹣c|= a+b+c .
【解答】解:∵a、b、c是△ABC的三边长,
∴a<b+c,b<a+c,c<a+b,
∴|a﹣b﹣c|+|b﹣c﹣a|+|a+b﹣c|=b+c﹣a+c+a﹣b+a+b﹣c=a+b+c;
故答案是:a+b+c.
19.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为偶数,则c= 10 .
【解答】解:∵a、b满足+(b﹣2)2=0,
∴a=10,b=2,
∵a、b、c为三角形的三边,
∴8<c<12,
∵第三边c为偶数,
∴c=10.
故答案为:10.
20.小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒能组成三角形的周长是 33 cm.
【解答】解:四根小木棒选出三根的情况有:5cm,6cm,11cm;5cm,6cm,16cm;5cm,11cm,16cm;6cm,11cm,16cm,共4种情况,
∵5+6=11,5+6<16,5+11=16,
∴构成三角形的情况有:6cm,11cm,16cm,1种情况,
此时三根木棒形成的三角形的周长=6+11+16=33(cm),
故答案为:33.
三.解答题(共5小题)
21.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
【解答】解:①∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|a﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴a=2,
∴△ABC的周长为:2+2+3=7,
∴△ABC是等腰三角形.
②∵a=5,b=2,c为整数,
∴5﹣2<c<2+5,
∴c的最小值为4,c的最大值为6,
∴△ABC的周长的最大值=5+2+6=13,最小值=5+2+4=11.
22.若△ABC的三边长分别为m﹣2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
【解答】解:(1)根据三角形的三边关系,
,
解得:3<m<5;
(2)因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m﹣2)+(2m+1)+8=3m+7=3×4+7=19.
23.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
【解答】解:∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD===4.8(cm),即AD的长度为4.8cm;
(2)方法一:如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
方法二:因为BE=BC=5,由(1)知AD=4.8,
所以S△ABE=BE AD=×5×4.8=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE)=AC﹣AB=8﹣6=2(cm),即△ACE和△ABE的周长的差是2cm.
24.如图,P为△ABC内任意一点,求证:AB+AC>PB+PC.
【解答】证明:延长BP交AC于点D,
在△ABD中,PB+PD<AB+AD①
在△PCD中,PC<PD+CD②
①+②得PB+PD+PC<AB+AD+PD+CD,
即PB+PC<AB+AC,
即:AB+AC>PB+PC.
25.观察以下图形,回答问题:
(1)图②有 3 个三角形;图③有 5 个三角形;图④有 7 个三角形;…猜测第七个图形中共有 13 个三角形.
(2)按上面的方法继续下去,第n个图形中有 (2n﹣1) 个三角形(用含n的代数式表示结论).
【解答】解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
