2022-2023学年苏科版数学八年级上册1.3 探索三角形全等的条件 同步练习(含解析)
文档属性
| 名称 | 2022-2023学年苏科版数学八年级上册1.3 探索三角形全等的条件 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 562.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览



文档简介
阶段练习:1.3.6运用SAS、ASA、AAS、SSS判定两个三角形全等(1)
-2022-2023学年苏科版数学八年级上册
一、选择题
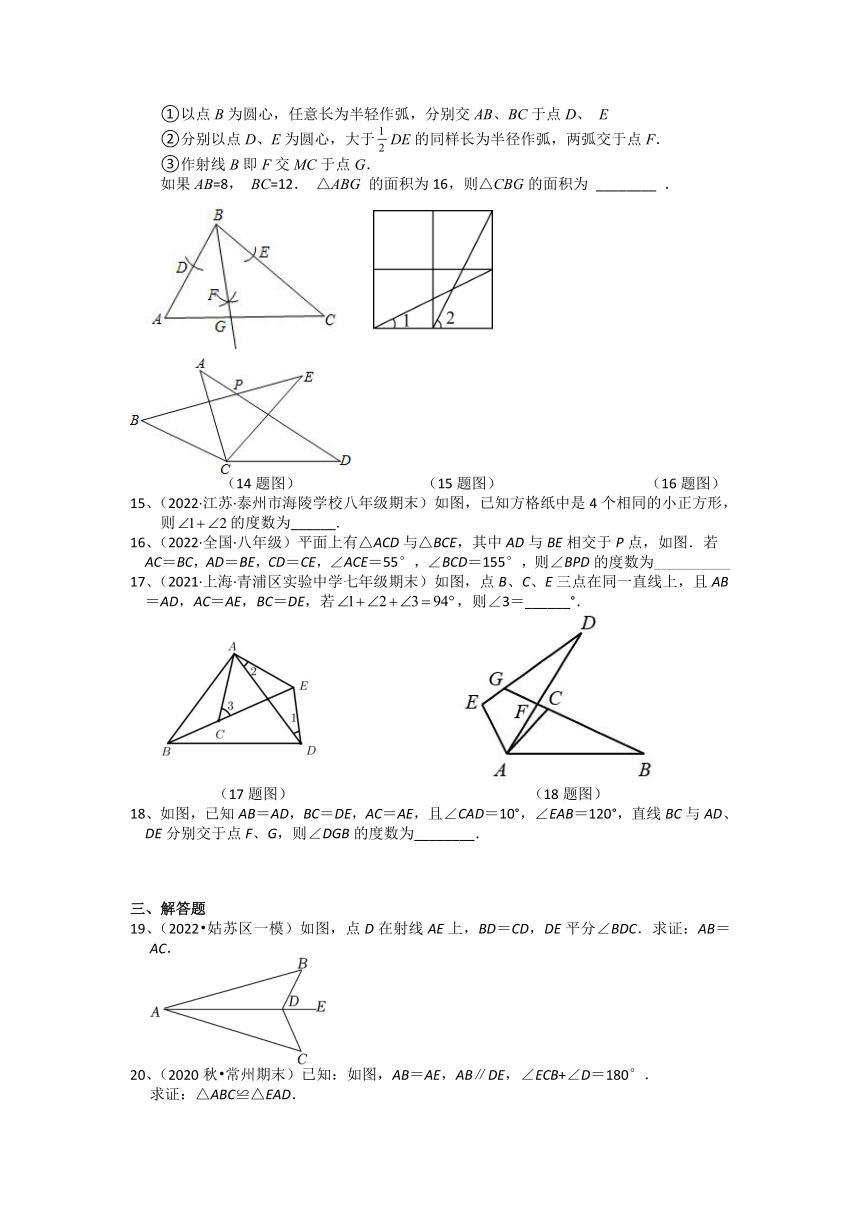
1、(2022·辽宁营口·八年级期末)如图,AC=DC,∠BCE=∠DCA,要使△ABC≌△DEC,不能添加下列选项中的( )
A.∠A=∠D B.BC=EC C.AB=DE D.∠B=∠E
(2题图) (3题图) (4题图)
2、如图,点,,,在同一条直线上,点,在直线的两侧,,,添加下列哪个条件后,仍不能判定出( )
A. B. C. D.
3、(2021秋 鼓楼区校级月考)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
4、(2022·宁夏固原·八年级期末)如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A.甲 B.乙 C.甲和乙 D.都不是
5、在和中,条件:①;②;③;④;⑤;⑥;则下列各组给出的条件不能保证的是( )
A.①②③ B.①②⑤ C.②⑤⑥ D.①③⑤
6、(2021秋 北海期末)把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
(6题图) (7题图) (8题图) (9题图)
7、如图,△ABC和△AED共顶点A,AD=AC,∠1=∠2,∠B=∠E. BC交AD于M,DE交AC于N,甲说:“一定有△ABC≌△AED.”乙说:“△ABM≌△AEN.”那么( )
A.甲、乙都对 B.甲、乙都不对 C.甲对、乙不对 D.甲不对、乙对
8、如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC C.∠B=∠E D.∠BAC=∠EAD
9、如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
10、如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
A.①②③ B.①③④ C.②③ D.①②③④
(10题图) (11题图) (12题图) (13题图)
二、填空题
11、(2022·宁夏·吴忠市第四中学八年级期末)如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是_______________(填3种答案)
12、(2020秋 梁溪区校级期中)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块.
13、(2022·全国·八年级)如图,已知,根据“SSS”,还需要一个条件________,可证明.
14、(2022·宁夏·吴忠市第四中学八年级期末)如图,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半轻作弧,分别交AB、BC于点D、 E
②分别以点D、E为圆心,大于DE的同样长为半径作弧,两弧交于点F.
③作射线B即F交MC于点G.
如果AB=8, BC=12. △ABG 的面积为16,则△CBG的面积为 ________ .
(14题图) (15题图) (16题图)
15、(2022·江苏·泰州市海陵学校八年级期末)如图,已知方格纸中是4个相同的小正方形,则的度数为______.
16、(2022·全国·八年级)平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为__________
17、(2021·上海·青浦区实验中学七年级期末)如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=______°.
(17题图) (18题图)
18、如图,已知AB=AD,BC=DE,AC=AE,且∠CAD=10°,∠EAB=120°,直线BC与AD、DE分别交于点F、G,则∠DGB的度数为________.
三、解答题
19、(2022 姑苏区一模)如图,点D在射线AE上,BD=CD,DE平分∠BDC.求证:AB=AC.
20、(2020秋 常州期末)已知:如图,AB=AE,AB∥DE,∠ECB+∠D=180°.
求证:△ABC≌△EAD.
21、(2020春 江阴市期中)如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
22、(2021春 宣汉县期末)如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
23、(2022·江西上饶·八年级期末)如图,已知五边形ABCDE的各边都相等,各内角也都相等,点F、G分别在边BC、CD上,且FC=GD.
(1)求证:ΔCDF ≌ ΔDEG;
(2)求∠EHF的大小.
24、(2022·江西赣州·八年级期末)如图,,点在上.
(1)求证:平分;(2)求证:.
25、(2022·全国·八年级阶段练习)如图,在△ABC与△ABD中,AC = BD,且CE = DE,AE = BE,AD与BC交于点E.
(1)求证:△ACE ≌ △BDE;
(2)若AC = 3,BC = 5,求△ACE的周长.
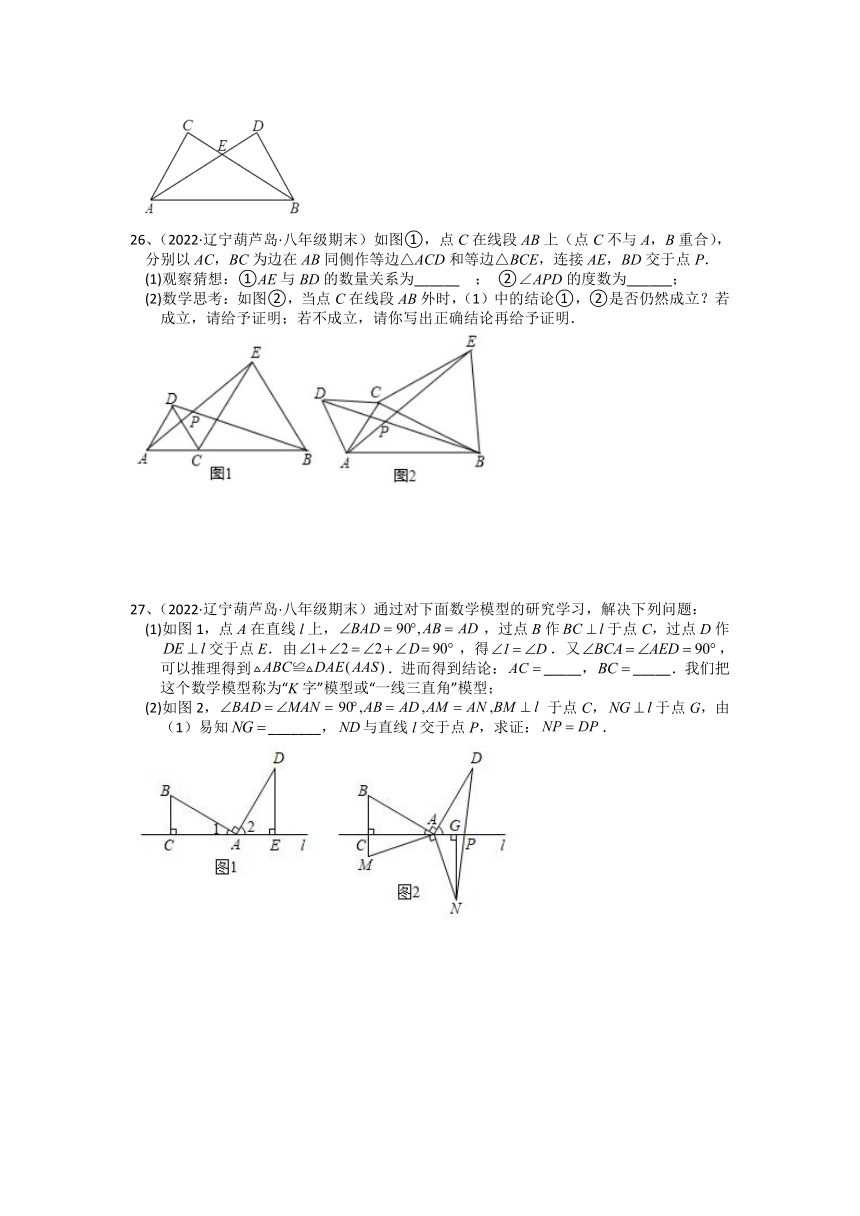
26、(2022·辽宁葫芦岛·八年级期末)如图①,点C在线段AB上(点C不与A,B重合),分别以AC,BC为边在AB同侧作等边△ACD和等边△BCE,连接AE,BD交于点P.
(1)观察猜想:①AE与BD的数量关系为______ ; ②∠APD的度数为______;
(2)数学思考:如图②,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
27、(2022·辽宁葫芦岛·八年级期末)通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,点A在直线l上,,过点B作于点C,过点D作交于点E.由,得.又,可以推理得到.进而得到结论:_____,_____.我们把这个数学模型称为“K字”模型或“一线三直角”模型;
(2)如图2,于点C,于点G,由(1)易知_______,与直线l交于点P,求证:.
阶段练习:1.3.6运用SAS、ASA、AAS、SSS判定两个三角形全等(1)
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·辽宁营口·八年级期末)如图,AC=DC,∠BCE=∠DCA,要使△ABC≌△DEC,不能添加下列选项中的( )
A.∠A=∠D B.BC=EC C.AB=DE D.∠B=∠E
【解析】根据已知条件可得,即,
∵AC=DC,∴已知三角形一角和角的一边,根据全等条件可得:
A. ∠A=∠D,可根据ASA证明,A正确; B. BC=EC,可根据SAS证明,B正确;
C. AB=DE,不能证明,C故错误; D. ∠B=∠E,根据AAS证明,D正确;
故选:C.
2、如图,点,,,在同一条直线上,点,在直线的两侧,,,添加下列哪个条件后,仍不能判定出( )
A. B. C. D.
【答案】A
解:,,
,,即,
当添加,即时,可根据“”判断;
当添加时,可根据“”判断;
当添加时,可根据“”判断.
故选:.
3、(2021秋 鼓楼区校级月考)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
【解析】∵在△ONC和△OMC中,∴△MOC≌△NOC(SSS),∴∠BOC=∠AOC,
故选:A.
4、(2022·宁夏固原·八年级期末)如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A.甲 B.乙 C.甲和乙 D.都不是
解:甲三角形夹b边的两角分别与已知三角形对应相等,故根据ASA可判定甲与△ABC全等;
乙三角形50°内角及所对边与△ABC对应相等且均有70°内角,可根据AAS判定乙与△ABC全等;
则与△ABC全等的有乙和甲, 故选:C.
5、在和中,条件:①;②;③;④;⑤;⑥;则下列各组给出的条件不能保证的是( )
A.①②③ B.①②⑤ C.②⑤⑥ D.①③⑤
【答案】D
解:A、①②③可以利用“SSS”证明△ABC≌△DEF,故本选项不符合;
B、①②⑤可以利用“SAS”证明△ABC≌△DEF,故本选项不符合;
C、②⑤⑥可以利用“AAS”证明△ABC≌△DEF,故本选项不符合;
D、①③⑤符合“SSA”,不能证明△ABC≌△DEF,故本选项符合.
故选:D.
6、(2021秋 北海期末)把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
【解析】∵∠CEA=∠ADB=∠CAB=90°,
∴∠ECA+∠EAC=∠EAC+∠DAB=∠DAB+∠DBA=90°,∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,∴△AEC≌△BAD,
∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE=3+5=8.故选:C.
7、如图,△ABC和△AED共顶点A,AD=AC,∠1=∠2,∠B=∠E. BC交AD于M,DE交AC于N,甲说:“一定有△ABC≌△AED.”乙说:“△ABM≌△AEN.”那么( )
A.甲、乙都对 B.甲、乙都不对 C.甲对、乙不对 D.甲不对、乙对
【答案】A
【详解】∵∠1=∠2,∴∠1+∠MAC=∠2+∠MAC,∴∠BAC=∠EAD,
在△BAC和△EAD中,,∴△BAC≌△EAD,∴甲说的正确;
∵△BAC≌△EAD(AAS),∴AB=AE,
在△BAM和△EAN中,,∴△BAM≌△EAN(ASA),∴乙说的正确;
故选A.
8、如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC C.∠B=∠E D.∠BAC=∠EAD
【答案】C
解:A.∵AB=AE,AC=AD,BC=ED,∴△ABC≌△AED(SSS),故A不符合题意;
B. ∵∠BAD=∠EAC,∴∠BAC=∠EAD.∵AB=AE,∠BAC=∠EAD ,AC=AD,
∴△ABC≌△AED(SAS),故B不符合题意;
C.不能判定△ABC≌△AED,故C符合题意.
D.∵AB=AE, ∠BAC=∠EAD,AC=AD,∴△ABC≌△AED(SAS),故D不符合题意.
故选C.
9、如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
【答案】C
【详解】解:∵AB∥CD,∴∠ABE=∠CDF,
在△ABE和△CDF中∴△ABE≌△CDF(SAS),∴AE=CF,
∵BE=DF,∴BE+EF=DF+EF,∴BF=DE,
在△ADE和△CBF中∴△ADE≌△CBF(SSS),∴AD=BC,
在△ABD和△CDB中,∴△ABD≌△CDB(SSS),
即3对全等三角形,故选:C.
10、如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
A.①②③ B.①③④ C.②③ D.①②③④
【答案】D
【解析】∵BF∥AC,∴∠C=∠CBF,
∵BC平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,∴AB=AC,
∵AD是△ABC的角平分线,∴BD=CD,AD⊥BC,故②③正确,
在△CDE与△DBF中,,∴△CDE≌△DBF,∴DE=DF,CE=BF,故①正确;
∵AE=2EC,∴AC=3EC=3BF,故④正确.
故选D.
二、填空题
11、(2022·宁夏·吴忠市第四中学八年级期末)如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是_______________(填3种答案)
【解析】添加∠A=∠F;要判定△ABC≌△FDE,已知AC=FE,AD=BF,则AB=CF,具备了两组边对应相等,故添加夹角 ∠A=∠F,利用SAS可证全等;
或添加AC∥EF得夹角∠A=∠F,利用SAS可证全等;
或添加BC=DE,利用SSS可证全等.
12、(2020秋 梁溪区校级期中)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块.
【解析】1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故答案为:2.
13、(2022·全国·八年级)如图,已知,根据“SSS”,还需要一个条件________,可证明.
【答案】(答案不唯一)
【详解】图形中隐含条件AB=BA,找出第三边BD和AC即可;
在△ABC和△BAD中 ,∴△ABC≌△BAD(SSS)
14、(2022·宁夏·吴忠市第四中学八年级期末)如图,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半轻作弧,分别交AB、BC于点D、 E
②分别以点D、E为圆心,大于DE的同样长为半径作弧,两弧交于点F.
③作射线B即F交MC于点G.
如果AB=8, BC=12. △ABG 的面积为16,则△CBG的面积为 ________ .
解:如图,过点G作GM⊥AB于点G,GN⊥AC于点N.
由作图可知BG平分∠ABC,
∵GM⊥BA,GN⊥BC,∴GM=GN,
∵=AB·GM=16,AB=8,∴GM=4,∴GN=GM=4,
∴=BC·GN=×12×4=24,故答案为:24.
15、(2022·江苏·泰州市海陵学校八年级期末)如图,已知方格纸中是4个相同的小正方形,则的度数为______.
解:如图,根据方格纸的性质,
在△ABD和△CBE中,∴△ABD≌△CBE(SAS),∴∠1=∠BAD,
∵∠BAD+∠2=90°,∴=90°.故答案为:90°.
16、(2022·全国·八年级)平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为__________
【详解】解:在△ACD和△BCE中,,∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,∴∠BCA+∠ECD=100°,∴∠BCA=∠ECD=50°,
∵∠ACE=55°,∴∠ACD=105°∴∠A+∠D=75°,∴∠B+∠D=75°,
∵∠BCD=155°,∴∠BPD=360°﹣75°﹣155°=130°,
17、(2021·上海·青浦区实验中学七年级期末)如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=______°.
【答案】47
【详解】解:在△ABC和△ADE中,,∴(SSS),
∴∠ABC=∠1,∠BAC=∠2,∴∠3=∠ABC+∠BAC=∠1+∠2,
∵,∴,∴. 故答案为:47.
18、如图,已知AB=AD,BC=DE,AC=AE,且∠CAD=10°,∠EAB=120°,直线BC与AD、DE分别交于点F、G,则∠DGB的度数为________.
解:∵AB=AD,BC=DE,AC=AE,∴△ABC≌△ADE,∴∠BAC=∠DAE,∠B=∠D;
∵∠EAB=120°,∴∠DAE+∠CAD+∠BAC=120°,
∵∠CAD=10°,∴∠BAC=(120°-10°)=55°,∴∠BAF=∠BAC+∠CAD=65°,
∵∠B=∠D,∠DFG=∠BFA,∴∠DGB=∠BAF =65°.
三、解答题
19、(2022 姑苏区一模)如图,点D在射线AE上,BD=CD,DE平分∠BDC.求证:AB=AC.
【分析】由“SAS”判定△ADC≌△ADB,得出AB=AC即可.
【解答】证明:∵DE平分∠BDC,∴∠BDE=∠CDE,∴∠ADB=∠ADC,
在△ADC和△ADB中,,∴△ADC≌△ADB(SAS),∴AB=AC.
20、(2020秋 常州期末)已知:如图,AB=AE,AB∥DE,∠ECB+∠D=180°.
求证:△ABC≌△EAD.
【分析】根据全等三角形的判定方法解答即可.
【解答】证明:∵AB∥DE,∴∠CAB=∠E,
∵∠ECB+∠D=180°,∠ECB+∠ACB=180°,∴∠D=∠ACB,
在△ABC与△EAD中,,∴△ABC≌△EAD(AAS).
21、(2020春 江阴市期中)如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
【解答】(1)证明:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠1=∠EAC,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,∴∠ABD=∠2=30°,
∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°.
22、(2021春 宣汉县期末)如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
【解答】(1)证明:∵AB∥DE,∴∠ABC=∠DEF,
在△ABC与△DEF中;∴△ABC≌△DEF(ASA);
(2)∵△ABC≌△DEF,∴BC=EF,∴BF+FC=EC+FC,∴BF=EC,
∵BE=10m,BF=3m,∴FC=10﹣3﹣3=4m.
23、(2022·江西上饶·八年级期末)如图,已知五边形ABCDE的各边都相等,各内角也都相等,点F、G分别在边BC、CD上,且FC=GD.
(1)求证:ΔCDF ≌ ΔDEG;
(2)求∠EHF的大小.
(1)证明:在ΔCDF与ΔDEG中
∵五边形ABCDE的各边都相等,各内角也都相等,∴CD=DE,∠FCD=∠GDE
又∵FC=GD;在△CDF和△DEG中,,∴ΔCDF ≌ ΔDEG(SAS);
(2)解:∵ΔCDF ≌ ΔDEG;∴∠FDC=∠GED
∴∠EHF=∠GED+∠HDE=∠FDC+∠HDE=∠CDE=
24、(2022·江西赣州·八年级期末)如图,,点在上.
(1)求证:平分;(2)求证:.
解:(1)在与中,∴;∴;即平分;
(2)由(1)
在与中,得;∴;∴
25、(2022·全国·八年级阶段练习)如图,在△ABC与△ABD中,AC = BD,且CE = DE,AE = BE,AD与BC交于点E.
(1)求证:△ACE ≌ △BDE;
(2)若AC = 3,BC = 5,求△ACE的周长.
【详解】证明:(1)在ACE和BDE中;∴ACE≌BDE
(2)∵AC = 3,BC = 5,AE = BE
∴ACE的周长为AC+CE+AE=AC+CE+BE=AC+BC=8
26、(2022·辽宁葫芦岛·八年级期末)如图①,点C在线段AB上(点C不与A,B重合),分别以AC,BC为边在AB同侧作等边△ACD和等边△BCE,连接AE,BD交于点P.
(1)观察猜想:①AE与BD的数量关系为______ ; ②∠APD的度数为______;
(2)数学思考:如图②,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
【答案】(1)①AE=BD;②60°;(2)上述结论成立.∠APD=60°,证明见解析
(1)解:∵△ACD和△CBE都是等边三角形,∴AC=DC,CE=CB,∠ACD=∠ECB=60°,
∵∠ACE=∠ACD+∠DCE,∠DCB=∠DCE+∠ECB,∴∠DCB=∠ACE,
∴△DCB≌△ACE,∴AE=BD,∠BDC=∠CAE,
又∵∠DOP=∠COA,∴∠APD=∠ACD=60°,故答案是:AE=BD,60°;
(2)上述结论成立,
∵△ACD,△BCE均为等边三角形,∴DC=AC,BC=EC,∠DCA=∠BCE=60°,
∴∠DCA+∠ACB=∠ACB+∠BCE,即∠DCB=∠ACE,
在△DCB和△ACE中,,
∴△DCB≌△ACE(SAS),∴DB=AE, ∠CDB=∠CAE,
如图,设BD与AC交于点O,易知∠DOC=∠AOP(对顶角相等),
∴∠CDB+∠DCA=∠CAE+∠DPA,∴∠DCA=∠DPA=60°,即∠APD=60°.
27、(2022·辽宁葫芦岛·八年级期末)通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,点A在直线l上,,过点B作于点C,过点D作交于点E.由,得.又,可以推理得到.进而得到结论:_____,_____.我们把这个数学模型称为“K字”模型或“一线三直角”模型;
(2)如图2,于点C,于点G,由(1)易知_______,与直线l交于点P,求证:.
(1)解:∵,∴AC=DE,BC=AE,故答案为DE,AE;
(2)证明:过D作DE⊥直线l于E,
∵,∴∠CAM+∠NAG=90°,
∵BM⊥l,∴∠MCA=90°,∴∠M+∠CAM=90°,∴∠M=∠NAG,
∵,∴∠AGN=90°,
在△MCA和△AGN中,,∴△MCA≌△AGN(AAS),∴AC=NG,
由(1)知,∴AC=DE,∴NG=DE,
在△NGP和△DEP中,,∴△NGP≌△DEP(AAS),∴NP=DP,
故答案为AC.
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·辽宁营口·八年级期末)如图,AC=DC,∠BCE=∠DCA,要使△ABC≌△DEC,不能添加下列选项中的( )
A.∠A=∠D B.BC=EC C.AB=DE D.∠B=∠E
(2题图) (3题图) (4题图)
2、如图,点,,,在同一条直线上,点,在直线的两侧,,,添加下列哪个条件后,仍不能判定出( )
A. B. C. D.
3、(2021秋 鼓楼区校级月考)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
4、(2022·宁夏固原·八年级期末)如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A.甲 B.乙 C.甲和乙 D.都不是
5、在和中,条件:①;②;③;④;⑤;⑥;则下列各组给出的条件不能保证的是( )
A.①②③ B.①②⑤ C.②⑤⑥ D.①③⑤
6、(2021秋 北海期末)把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
(6题图) (7题图) (8题图) (9题图)
7、如图,△ABC和△AED共顶点A,AD=AC,∠1=∠2,∠B=∠E. BC交AD于M,DE交AC于N,甲说:“一定有△ABC≌△AED.”乙说:“△ABM≌△AEN.”那么( )
A.甲、乙都对 B.甲、乙都不对 C.甲对、乙不对 D.甲不对、乙对
8、如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC C.∠B=∠E D.∠BAC=∠EAD
9、如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
10、如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
A.①②③ B.①③④ C.②③ D.①②③④
(10题图) (11题图) (12题图) (13题图)
二、填空题
11、(2022·宁夏·吴忠市第四中学八年级期末)如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是_______________(填3种答案)
12、(2020秋 梁溪区校级期中)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块.
13、(2022·全国·八年级)如图,已知,根据“SSS”,还需要一个条件________,可证明.
14、(2022·宁夏·吴忠市第四中学八年级期末)如图,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半轻作弧,分别交AB、BC于点D、 E
②分别以点D、E为圆心,大于DE的同样长为半径作弧,两弧交于点F.
③作射线B即F交MC于点G.
如果AB=8, BC=12. △ABG 的面积为16,则△CBG的面积为 ________ .
(14题图) (15题图) (16题图)
15、(2022·江苏·泰州市海陵学校八年级期末)如图,已知方格纸中是4个相同的小正方形,则的度数为______.
16、(2022·全国·八年级)平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为__________
17、(2021·上海·青浦区实验中学七年级期末)如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=______°.
(17题图) (18题图)
18、如图,已知AB=AD,BC=DE,AC=AE,且∠CAD=10°,∠EAB=120°,直线BC与AD、DE分别交于点F、G,则∠DGB的度数为________.
三、解答题
19、(2022 姑苏区一模)如图,点D在射线AE上,BD=CD,DE平分∠BDC.求证:AB=AC.
20、(2020秋 常州期末)已知:如图,AB=AE,AB∥DE,∠ECB+∠D=180°.
求证:△ABC≌△EAD.
21、(2020春 江阴市期中)如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
22、(2021春 宣汉县期末)如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
23、(2022·江西上饶·八年级期末)如图,已知五边形ABCDE的各边都相等,各内角也都相等,点F、G分别在边BC、CD上,且FC=GD.
(1)求证:ΔCDF ≌ ΔDEG;
(2)求∠EHF的大小.
24、(2022·江西赣州·八年级期末)如图,,点在上.
(1)求证:平分;(2)求证:.
25、(2022·全国·八年级阶段练习)如图,在△ABC与△ABD中,AC = BD,且CE = DE,AE = BE,AD与BC交于点E.
(1)求证:△ACE ≌ △BDE;
(2)若AC = 3,BC = 5,求△ACE的周长.
26、(2022·辽宁葫芦岛·八年级期末)如图①,点C在线段AB上(点C不与A,B重合),分别以AC,BC为边在AB同侧作等边△ACD和等边△BCE,连接AE,BD交于点P.
(1)观察猜想:①AE与BD的数量关系为______ ; ②∠APD的度数为______;
(2)数学思考:如图②,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
27、(2022·辽宁葫芦岛·八年级期末)通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,点A在直线l上,,过点B作于点C,过点D作交于点E.由,得.又,可以推理得到.进而得到结论:_____,_____.我们把这个数学模型称为“K字”模型或“一线三直角”模型;
(2)如图2,于点C,于点G,由(1)易知_______,与直线l交于点P,求证:.
阶段练习:1.3.6运用SAS、ASA、AAS、SSS判定两个三角形全等(1)
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·辽宁营口·八年级期末)如图,AC=DC,∠BCE=∠DCA,要使△ABC≌△DEC,不能添加下列选项中的( )
A.∠A=∠D B.BC=EC C.AB=DE D.∠B=∠E
【解析】根据已知条件可得,即,
∵AC=DC,∴已知三角形一角和角的一边,根据全等条件可得:
A. ∠A=∠D,可根据ASA证明,A正确; B. BC=EC,可根据SAS证明,B正确;
C. AB=DE,不能证明,C故错误; D. ∠B=∠E,根据AAS证明,D正确;
故选:C.
2、如图,点,,,在同一条直线上,点,在直线的两侧,,,添加下列哪个条件后,仍不能判定出( )
A. B. C. D.
【答案】A
解:,,
,,即,
当添加,即时,可根据“”判断;
当添加时,可根据“”判断;
当添加时,可根据“”判断.
故选:.
3、(2021秋 鼓楼区校级月考)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
【解析】∵在△ONC和△OMC中,∴△MOC≌△NOC(SSS),∴∠BOC=∠AOC,
故选:A.
4、(2022·宁夏固原·八年级期末)如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A.甲 B.乙 C.甲和乙 D.都不是
解:甲三角形夹b边的两角分别与已知三角形对应相等,故根据ASA可判定甲与△ABC全等;
乙三角形50°内角及所对边与△ABC对应相等且均有70°内角,可根据AAS判定乙与△ABC全等;
则与△ABC全等的有乙和甲, 故选:C.
5、在和中,条件:①;②;③;④;⑤;⑥;则下列各组给出的条件不能保证的是( )
A.①②③ B.①②⑤ C.②⑤⑥ D.①③⑤
【答案】D
解:A、①②③可以利用“SSS”证明△ABC≌△DEF,故本选项不符合;
B、①②⑤可以利用“SAS”证明△ABC≌△DEF,故本选项不符合;
C、②⑤⑥可以利用“AAS”证明△ABC≌△DEF,故本选项不符合;
D、①③⑤符合“SSA”,不能证明△ABC≌△DEF,故本选项符合.
故选:D.
6、(2021秋 北海期末)把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
【解析】∵∠CEA=∠ADB=∠CAB=90°,
∴∠ECA+∠EAC=∠EAC+∠DAB=∠DAB+∠DBA=90°,∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,∴△AEC≌△BAD,
∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE=3+5=8.故选:C.
7、如图,△ABC和△AED共顶点A,AD=AC,∠1=∠2,∠B=∠E. BC交AD于M,DE交AC于N,甲说:“一定有△ABC≌△AED.”乙说:“△ABM≌△AEN.”那么( )
A.甲、乙都对 B.甲、乙都不对 C.甲对、乙不对 D.甲不对、乙对
【答案】A
【详解】∵∠1=∠2,∴∠1+∠MAC=∠2+∠MAC,∴∠BAC=∠EAD,
在△BAC和△EAD中,,∴△BAC≌△EAD,∴甲说的正确;
∵△BAC≌△EAD(AAS),∴AB=AE,
在△BAM和△EAN中,,∴△BAM≌△EAN(ASA),∴乙说的正确;
故选A.
8、如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC C.∠B=∠E D.∠BAC=∠EAD
【答案】C
解:A.∵AB=AE,AC=AD,BC=ED,∴△ABC≌△AED(SSS),故A不符合题意;
B. ∵∠BAD=∠EAC,∴∠BAC=∠EAD.∵AB=AE,∠BAC=∠EAD ,AC=AD,
∴△ABC≌△AED(SAS),故B不符合题意;
C.不能判定△ABC≌△AED,故C符合题意.
D.∵AB=AE, ∠BAC=∠EAD,AC=AD,∴△ABC≌△AED(SAS),故D不符合题意.
故选C.
9、如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
【答案】C
【详解】解:∵AB∥CD,∴∠ABE=∠CDF,
在△ABE和△CDF中∴△ABE≌△CDF(SAS),∴AE=CF,
∵BE=DF,∴BE+EF=DF+EF,∴BF=DE,
在△ADE和△CBF中∴△ADE≌△CBF(SSS),∴AD=BC,
在△ABD和△CDB中,∴△ABD≌△CDB(SSS),
即3对全等三角形,故选:C.
10、如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
A.①②③ B.①③④ C.②③ D.①②③④
【答案】D
【解析】∵BF∥AC,∴∠C=∠CBF,
∵BC平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,∴AB=AC,
∵AD是△ABC的角平分线,∴BD=CD,AD⊥BC,故②③正确,
在△CDE与△DBF中,,∴△CDE≌△DBF,∴DE=DF,CE=BF,故①正确;
∵AE=2EC,∴AC=3EC=3BF,故④正确.
故选D.
二、填空题
11、(2022·宁夏·吴忠市第四中学八年级期末)如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是_______________(填3种答案)
【解析】添加∠A=∠F;要判定△ABC≌△FDE,已知AC=FE,AD=BF,则AB=CF,具备了两组边对应相等,故添加夹角 ∠A=∠F,利用SAS可证全等;
或添加AC∥EF得夹角∠A=∠F,利用SAS可证全等;
或添加BC=DE,利用SSS可证全等.
12、(2020秋 梁溪区校级期中)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块.
【解析】1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故答案为:2.
13、(2022·全国·八年级)如图,已知,根据“SSS”,还需要一个条件________,可证明.
【答案】(答案不唯一)
【详解】图形中隐含条件AB=BA,找出第三边BD和AC即可;
在△ABC和△BAD中 ,∴△ABC≌△BAD(SSS)
14、(2022·宁夏·吴忠市第四中学八年级期末)如图,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半轻作弧,分别交AB、BC于点D、 E
②分别以点D、E为圆心,大于DE的同样长为半径作弧,两弧交于点F.
③作射线B即F交MC于点G.
如果AB=8, BC=12. △ABG 的面积为16,则△CBG的面积为 ________ .
解:如图,过点G作GM⊥AB于点G,GN⊥AC于点N.
由作图可知BG平分∠ABC,
∵GM⊥BA,GN⊥BC,∴GM=GN,
∵=AB·GM=16,AB=8,∴GM=4,∴GN=GM=4,
∴=BC·GN=×12×4=24,故答案为:24.
15、(2022·江苏·泰州市海陵学校八年级期末)如图,已知方格纸中是4个相同的小正方形,则的度数为______.
解:如图,根据方格纸的性质,
在△ABD和△CBE中,∴△ABD≌△CBE(SAS),∴∠1=∠BAD,
∵∠BAD+∠2=90°,∴=90°.故答案为:90°.
16、(2022·全国·八年级)平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为__________
【详解】解:在△ACD和△BCE中,,∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,∴∠BCA+∠ECD=100°,∴∠BCA=∠ECD=50°,
∵∠ACE=55°,∴∠ACD=105°∴∠A+∠D=75°,∴∠B+∠D=75°,
∵∠BCD=155°,∴∠BPD=360°﹣75°﹣155°=130°,
17、(2021·上海·青浦区实验中学七年级期末)如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=______°.
【答案】47
【详解】解:在△ABC和△ADE中,,∴(SSS),
∴∠ABC=∠1,∠BAC=∠2,∴∠3=∠ABC+∠BAC=∠1+∠2,
∵,∴,∴. 故答案为:47.
18、如图,已知AB=AD,BC=DE,AC=AE,且∠CAD=10°,∠EAB=120°,直线BC与AD、DE分别交于点F、G,则∠DGB的度数为________.
解:∵AB=AD,BC=DE,AC=AE,∴△ABC≌△ADE,∴∠BAC=∠DAE,∠B=∠D;
∵∠EAB=120°,∴∠DAE+∠CAD+∠BAC=120°,
∵∠CAD=10°,∴∠BAC=(120°-10°)=55°,∴∠BAF=∠BAC+∠CAD=65°,
∵∠B=∠D,∠DFG=∠BFA,∴∠DGB=∠BAF =65°.
三、解答题
19、(2022 姑苏区一模)如图,点D在射线AE上,BD=CD,DE平分∠BDC.求证:AB=AC.
【分析】由“SAS”判定△ADC≌△ADB,得出AB=AC即可.
【解答】证明:∵DE平分∠BDC,∴∠BDE=∠CDE,∴∠ADB=∠ADC,
在△ADC和△ADB中,,∴△ADC≌△ADB(SAS),∴AB=AC.
20、(2020秋 常州期末)已知:如图,AB=AE,AB∥DE,∠ECB+∠D=180°.
求证:△ABC≌△EAD.
【分析】根据全等三角形的判定方法解答即可.
【解答】证明:∵AB∥DE,∴∠CAB=∠E,
∵∠ECB+∠D=180°,∠ECB+∠ACB=180°,∴∠D=∠ACB,
在△ABC与△EAD中,,∴△ABC≌△EAD(AAS).
21、(2020春 江阴市期中)如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
【解答】(1)证明:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠1=∠EAC,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,∴∠ABD=∠2=30°,
∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°.
22、(2021春 宣汉县期末)如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
【解答】(1)证明:∵AB∥DE,∴∠ABC=∠DEF,
在△ABC与△DEF中;∴△ABC≌△DEF(ASA);
(2)∵△ABC≌△DEF,∴BC=EF,∴BF+FC=EC+FC,∴BF=EC,
∵BE=10m,BF=3m,∴FC=10﹣3﹣3=4m.
23、(2022·江西上饶·八年级期末)如图,已知五边形ABCDE的各边都相等,各内角也都相等,点F、G分别在边BC、CD上,且FC=GD.
(1)求证:ΔCDF ≌ ΔDEG;
(2)求∠EHF的大小.
(1)证明:在ΔCDF与ΔDEG中
∵五边形ABCDE的各边都相等,各内角也都相等,∴CD=DE,∠FCD=∠GDE
又∵FC=GD;在△CDF和△DEG中,,∴ΔCDF ≌ ΔDEG(SAS);
(2)解:∵ΔCDF ≌ ΔDEG;∴∠FDC=∠GED
∴∠EHF=∠GED+∠HDE=∠FDC+∠HDE=∠CDE=
24、(2022·江西赣州·八年级期末)如图,,点在上.
(1)求证:平分;(2)求证:.
解:(1)在与中,∴;∴;即平分;
(2)由(1)
在与中,得;∴;∴
25、(2022·全国·八年级阶段练习)如图,在△ABC与△ABD中,AC = BD,且CE = DE,AE = BE,AD与BC交于点E.
(1)求证:△ACE ≌ △BDE;
(2)若AC = 3,BC = 5,求△ACE的周长.
【详解】证明:(1)在ACE和BDE中;∴ACE≌BDE
(2)∵AC = 3,BC = 5,AE = BE
∴ACE的周长为AC+CE+AE=AC+CE+BE=AC+BC=8
26、(2022·辽宁葫芦岛·八年级期末)如图①,点C在线段AB上(点C不与A,B重合),分别以AC,BC为边在AB同侧作等边△ACD和等边△BCE,连接AE,BD交于点P.
(1)观察猜想:①AE与BD的数量关系为______ ; ②∠APD的度数为______;
(2)数学思考:如图②,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
【答案】(1)①AE=BD;②60°;(2)上述结论成立.∠APD=60°,证明见解析
(1)解:∵△ACD和△CBE都是等边三角形,∴AC=DC,CE=CB,∠ACD=∠ECB=60°,
∵∠ACE=∠ACD+∠DCE,∠DCB=∠DCE+∠ECB,∴∠DCB=∠ACE,
∴△DCB≌△ACE,∴AE=BD,∠BDC=∠CAE,
又∵∠DOP=∠COA,∴∠APD=∠ACD=60°,故答案是:AE=BD,60°;
(2)上述结论成立,
∵△ACD,△BCE均为等边三角形,∴DC=AC,BC=EC,∠DCA=∠BCE=60°,
∴∠DCA+∠ACB=∠ACB+∠BCE,即∠DCB=∠ACE,
在△DCB和△ACE中,,
∴△DCB≌△ACE(SAS),∴DB=AE, ∠CDB=∠CAE,
如图,设BD与AC交于点O,易知∠DOC=∠AOP(对顶角相等),
∴∠CDB+∠DCA=∠CAE+∠DPA,∴∠DCA=∠DPA=60°,即∠APD=60°.
27、(2022·辽宁葫芦岛·八年级期末)通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,点A在直线l上,,过点B作于点C,过点D作交于点E.由,得.又,可以推理得到.进而得到结论:_____,_____.我们把这个数学模型称为“K字”模型或“一线三直角”模型;
(2)如图2,于点C,于点G,由(1)易知_______,与直线l交于点P,求证:.
(1)解:∵,∴AC=DE,BC=AE,故答案为DE,AE;
(2)证明:过D作DE⊥直线l于E,
∵,∴∠CAM+∠NAG=90°,
∵BM⊥l,∴∠MCA=90°,∴∠M+∠CAM=90°,∴∠M=∠NAG,
∵,∴∠AGN=90°,
在△MCA和△AGN中,,∴△MCA≌△AGN(AAS),∴AC=NG,
由(1)知,∴AC=DE,∴NG=DE,
在△NGP和△DEP中,,∴△NGP≌△DEP(AAS),∴NP=DP,
故答案为AC.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
