广东省汕头市龙湖实验中学2022-2023学年八年级上学期开学考试数学试题(word版含答案)
文档属性
| 名称 | 广东省汕头市龙湖实验中学2022-2023学年八年级上学期开学考试数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 519.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 13:29:20 | ||
图片预览


文档简介
2022-2023学年度上学期开学检测卷
初二数学科
选择题(本题共10小题,每小题3分,共30分)
1.下列选项的汽车标注图案中,可以看出由图案中的一个基本图形经过平移得到的是( )
A. B.C. D.
2.下列调查适用抽样调查的是( )
A.了解全国人民对垃圾分类的赞同情况 B.疫情期间,对某校到校学生进行体温检测
C.某单位职工健康检查 D.检测长征火箭的零件质量
3.如图,直线,一直角三角板ABC(∠ACB=900 )放在平行线上,两直角边分别与、交于点D、E,现测得∠1=750,则∠2的度数为( )
A.15° B.25° C.30° D.35°
4.若是方程的解,则的值为( )
A.1 B. C.7 D.
5.已知关于x,y的方程组的解是,则方程组的解是( )
A. B. C. D.
6.对于实数,我们规定表示不大于的最大整数,例如,,,若,则的取值可以是( )
A. B. C. D.
7.根据不等式的性质,下列变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
8.在平面直角坐标系中,点在第四象限内,则的取值可以是( )
A.1 B. C.0 D.2或﹣2
9.点(2,﹣1)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.其中一道题,原文是:“今三人共车,两车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B. C. D.
二.填空题(本大题共7小题,每小题4分,共28分)
11.已知,,则_______.
12.点P(a+5,a﹣1)是第四象限的点,且到x轴的距离为2,那么P的坐标为___.
13.如图,把一张长方形纸条沿折叠,若,则____.
14.某班思政课上举行了普法知识竞赛,共有30道题,规定答对一题得4分,答错或者不答扣1分,在这次竞赛中小明要不低于90分,则他至少需要答对______道题.
15.如图,三条直线,,相交于点,若,则______度.
16.若关于x、y的二元一次方程组的解也是二元一次方程的解,则k的值为_______.
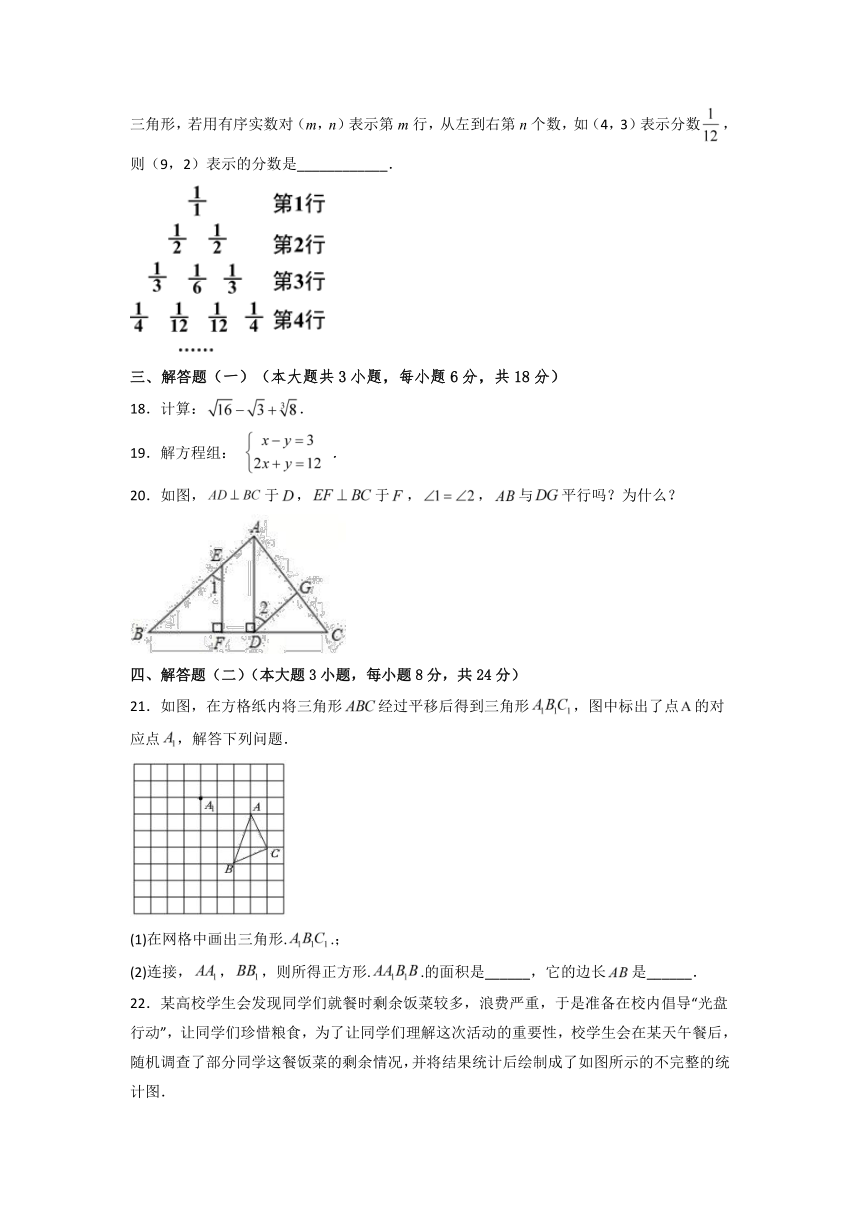
17.将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称为莱布尼茨三角形,若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数,则(9,2)表示的分数是____________.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.计算:.
19.解方程组: .
20.如图,于,于,,与平行吗?为什么?
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图,在方格纸内将三角形经过平移后得到三角形,图中标出了点的对应点,解答下列问题.
(1)在网格中画出三角形..;
(2)连接,,,则所得正方形..的面积是______,它的边长是______.
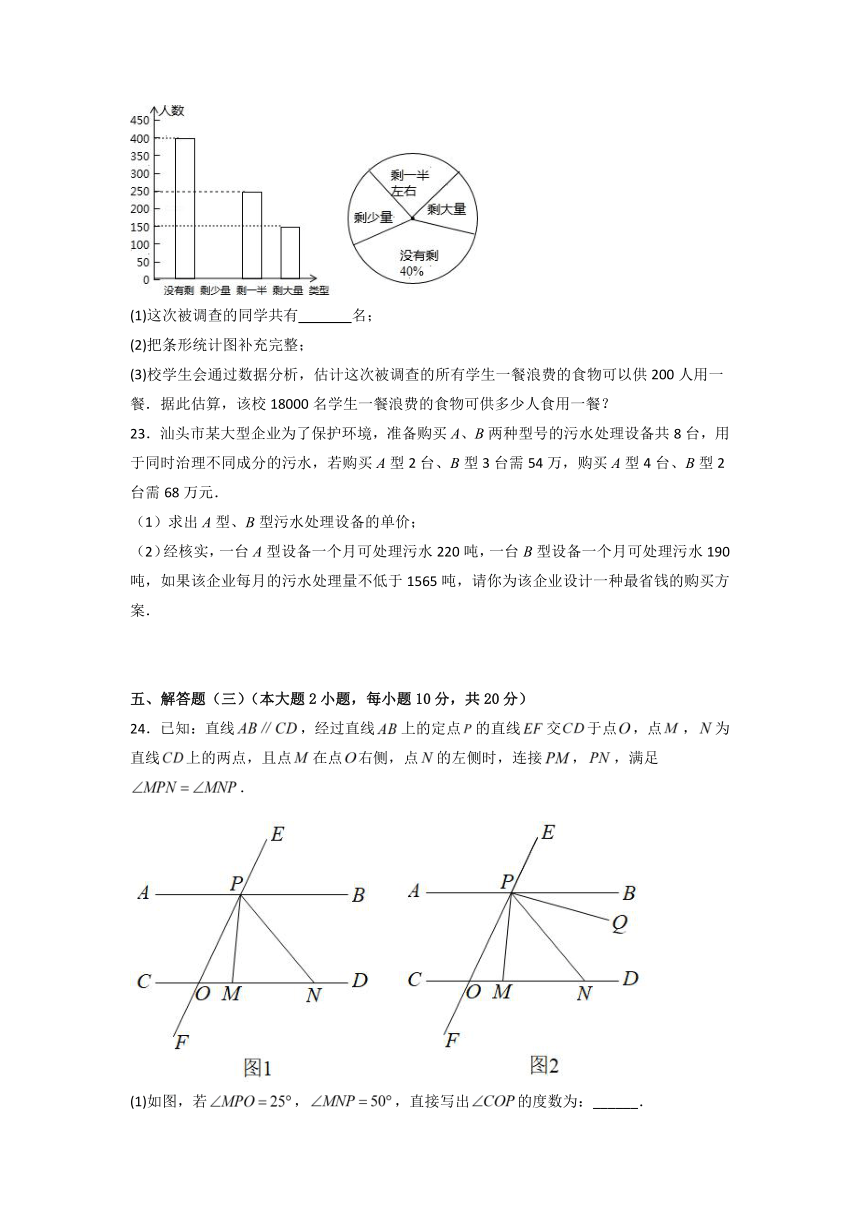
22.某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
23.汕头市某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.已知:直线,经过直线上的定点的直线交于点,点,为直线上的两点,且点在点右侧,点的左侧时,连接,,满足.
(1)如图,若,,直接写出的度数为:______.
(2)如图,射线为的角平分线,用等式表示与之间的数量关系,并证明.
25.在平面直角坐标系中,O为原点,点A(1,0),点B(0,3),
(1)如图①,三角形AOB的面积为 ;
(2)如图①,在x轴上是否存在点C,使三角形ABC的面积等于6,若存在,求点C的坐标;若不存在,请说明理由;
(3)如图②,将线段AB向右平移3个单位长度,再向上平移2个单位长度,得到线段A1B1,求三角形OA1B1的面积.
参考答案:
1.B 2.A 3.A 4.C 5.C
6.B 7.C 8.B 9.D 10.D
11. 12.(4,﹣2) 13.50°##50度 14.24 15. 16.2 17.
18..解:
.
19.解:,
+,可得3x=15,
解得x=5,
把x=5代入,解得y=2,
∴原方程组的解是.
20. 与平行,理由如下:
∵于,
∴,
∵于,
∴,
∴,
∴,
∴,
又∵,
∴,
∴.
21.(1)解:如图:即为所求;
(2)解:正方形的面积,它的边长是; 故答案为:,.
22.解:(1)这次被调查的同学共有400÷40%=1000(名)
故答案为:1000
(2)剩少量的人数是:1000-400-250-150=200(名),
(3)
答:该校1800名学生一餐浪费的食物可供3600人食用一餐.
23.设A型污水处理设备的单价为x万元,B型污水处理设备的单价为y万元,根据题意可得:,
解得:.
答:A型污水处理设备的单价为12万元,B型污水处理设备的单价为10万元;
(2)设购进a台A型污水处理器,根据题意可得:
220a+190(8﹣a)≥1565,解得:a≥1.5,
A型污水处理设备单价比B型污水处理设备单价高,
A型污水处理设备买越少,越省钱,
购进2台A型污水处理设备,购进6台B型污水处理设备最省钱.
24.
(1),,.,,.
(2)结论:.理由:,,.又射线为的角平分线,.,..即.
25.解:(1)∵点A(1,0),点B(0,3),
∴OA=1,OB=3,
∴S△AOB=·OA·OB=,
故答案为:;
(2)存在,
设点C的坐标为(a,0),,
若点C在x轴的正半轴上,则,
三角形ABC的面积,
解得,
∴点C的坐标为(5,0);
若点C在x轴的负半轴上,则,
三角形ABC的面积,
解得,
∴点C的坐标为(,0);
∴点C的坐标为(5,0)或(,0);
(2)由平移可知点A1(4,2)、B1(3,5),
过点A1作x轴的垂线,垂足为C,过点B1作y轴的垂线,垂足为D,两条垂线相交于点E,
则,
∴三角形OA1B1的面积.
初二数学科
选择题(本题共10小题,每小题3分,共30分)
1.下列选项的汽车标注图案中,可以看出由图案中的一个基本图形经过平移得到的是( )
A. B.C. D.
2.下列调查适用抽样调查的是( )
A.了解全国人民对垃圾分类的赞同情况 B.疫情期间,对某校到校学生进行体温检测
C.某单位职工健康检查 D.检测长征火箭的零件质量
3.如图,直线,一直角三角板ABC(∠ACB=900 )放在平行线上,两直角边分别与、交于点D、E,现测得∠1=750,则∠2的度数为( )
A.15° B.25° C.30° D.35°
4.若是方程的解,则的值为( )
A.1 B. C.7 D.
5.已知关于x,y的方程组的解是,则方程组的解是( )
A. B. C. D.
6.对于实数,我们规定表示不大于的最大整数,例如,,,若,则的取值可以是( )
A. B. C. D.
7.根据不等式的性质,下列变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
8.在平面直角坐标系中,点在第四象限内,则的取值可以是( )
A.1 B. C.0 D.2或﹣2
9.点(2,﹣1)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.其中一道题,原文是:“今三人共车,两车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B. C. D.
二.填空题(本大题共7小题,每小题4分,共28分)
11.已知,,则_______.
12.点P(a+5,a﹣1)是第四象限的点,且到x轴的距离为2,那么P的坐标为___.
13.如图,把一张长方形纸条沿折叠,若,则____.
14.某班思政课上举行了普法知识竞赛,共有30道题,规定答对一题得4分,答错或者不答扣1分,在这次竞赛中小明要不低于90分,则他至少需要答对______道题.
15.如图,三条直线,,相交于点,若,则______度.
16.若关于x、y的二元一次方程组的解也是二元一次方程的解,则k的值为_______.
17.将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称为莱布尼茨三角形,若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数,则(9,2)表示的分数是____________.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.计算:.
19.解方程组: .
20.如图,于,于,,与平行吗?为什么?
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图,在方格纸内将三角形经过平移后得到三角形,图中标出了点的对应点,解答下列问题.
(1)在网格中画出三角形..;
(2)连接,,,则所得正方形..的面积是______,它的边长是______.
22.某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
23.汕头市某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.已知:直线,经过直线上的定点的直线交于点,点,为直线上的两点,且点在点右侧,点的左侧时,连接,,满足.
(1)如图,若,,直接写出的度数为:______.
(2)如图,射线为的角平分线,用等式表示与之间的数量关系,并证明.
25.在平面直角坐标系中,O为原点,点A(1,0),点B(0,3),
(1)如图①,三角形AOB的面积为 ;
(2)如图①,在x轴上是否存在点C,使三角形ABC的面积等于6,若存在,求点C的坐标;若不存在,请说明理由;
(3)如图②,将线段AB向右平移3个单位长度,再向上平移2个单位长度,得到线段A1B1,求三角形OA1B1的面积.
参考答案:
1.B 2.A 3.A 4.C 5.C
6.B 7.C 8.B 9.D 10.D
11. 12.(4,﹣2) 13.50°##50度 14.24 15. 16.2 17.
18..解:
.
19.解:,
+,可得3x=15,
解得x=5,
把x=5代入,解得y=2,
∴原方程组的解是.
20. 与平行,理由如下:
∵于,
∴,
∵于,
∴,
∴,
∴,
∴,
又∵,
∴,
∴.
21.(1)解:如图:即为所求;
(2)解:正方形的面积,它的边长是; 故答案为:,.
22.解:(1)这次被调查的同学共有400÷40%=1000(名)
故答案为:1000
(2)剩少量的人数是:1000-400-250-150=200(名),
(3)
答:该校1800名学生一餐浪费的食物可供3600人食用一餐.
23.设A型污水处理设备的单价为x万元,B型污水处理设备的单价为y万元,根据题意可得:,
解得:.
答:A型污水处理设备的单价为12万元,B型污水处理设备的单价为10万元;
(2)设购进a台A型污水处理器,根据题意可得:
220a+190(8﹣a)≥1565,解得:a≥1.5,
A型污水处理设备单价比B型污水处理设备单价高,
A型污水处理设备买越少,越省钱,
购进2台A型污水处理设备,购进6台B型污水处理设备最省钱.
24.
(1),,.,,.
(2)结论:.理由:,,.又射线为的角平分线,.,..即.
25.解:(1)∵点A(1,0),点B(0,3),
∴OA=1,OB=3,
∴S△AOB=·OA·OB=,
故答案为:;
(2)存在,
设点C的坐标为(a,0),,
若点C在x轴的正半轴上,则,
三角形ABC的面积,
解得,
∴点C的坐标为(5,0);
若点C在x轴的负半轴上,则,
三角形ABC的面积,
解得,
∴点C的坐标为(,0);
∴点C的坐标为(5,0)或(,0);
(2)由平移可知点A1(4,2)、B1(3,5),
过点A1作x轴的垂线,垂足为C,过点B1作y轴的垂线,垂足为D,两条垂线相交于点E,
则,
∴三角形OA1B1的面积.
同课章节目录
