22.3第1课时 二次函数与图形面积问题 课件 (共16张PPT)
文档属性
| 名称 | 22.3第1课时 二次函数与图形面积问题 课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 938.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
22.3第1课时
二次函数与图形面积问题
人教版 九年级上册
教学目标
教学目标:
1.能够从实际问题中抽象出二次函数关系.(重点)
2.会运用二次函数知识求实际问题中的最大值或最小值,解决实际问题.(难点)
3.能应用二次函数的性质解决图形中的最大面积问题.
新知导入
思考 排球运动员从地面竖直向上抛出排球,排球的高度 h(单位:m)与排球的运动时间 t(单位:s)之间的关系式是h= 20t - 5t 2 (0≤t≤4).排球的运动时间是多少时,排球最高?排球运动中的最大高度是多少?
0
h
t
4
新知讲解
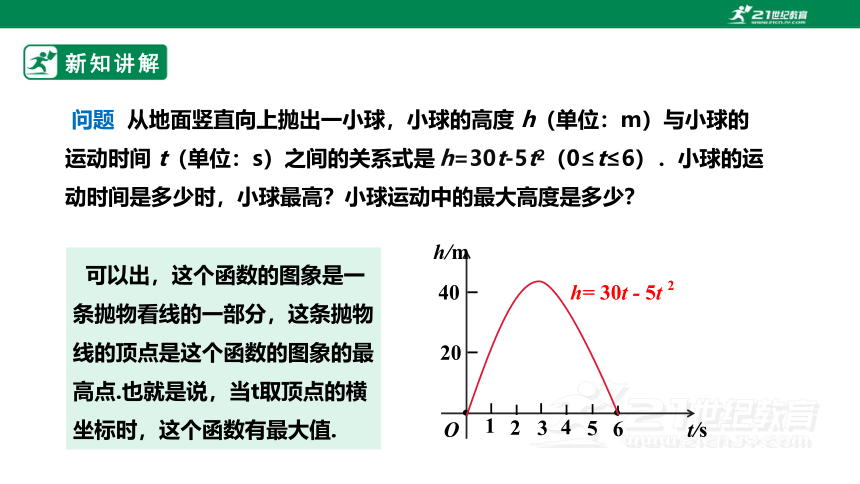
问题 从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 h=30t-5t2(0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
可以出,这个函数的图象是一条抛物看线的一部分,这条抛物线的顶点是这个函数的图象的最高点.也就是说,当t取顶点的横坐标时,这个函数有最大值.
新知讲解
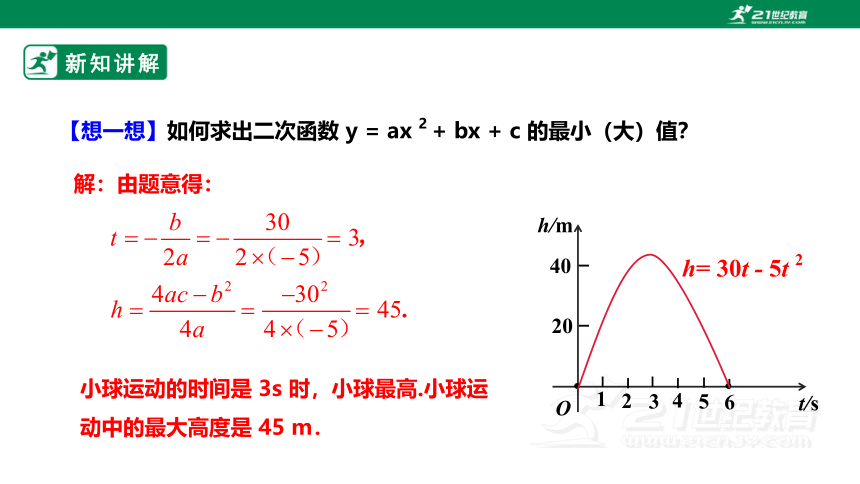
小球运动的时间是 3s 时,小球最高.小球运动中的最大高度是 45 m.
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
解:由题意得:
【想一想】如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
总结归纳
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值 .
新知讲解
探究1 用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
分析 先写出 S 关于 l 的函数解析式,再求出使 S 最大 的l 值.
解: 矩形场地周长为 60 m ,一边长为 l m,所以另一边长为 m,
场地的面积 S =l(30-l)
即 S=-l2+30l (0因此,当 时,
S有最大值.
方法总结
二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
课堂练习
1.用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形菜园的最大面积是________.
A. 6厘米 B. 12厘米 C. 24厘米 D. 36厘米
2.某种正方形合金板材的成本y(元)与它的面积成正比,设边长为厘米,当x=3时,y=18那么当成本为78元时,边长为( )
A
课堂练习
3.用长12 m的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是( )
A.9 m2 B.2 m2 C.6 m2 D.8 m2
C
课堂练习
解:设一直角边长为x,则另一直角边长为 ,依题意得:
4.已知直角三角形的两直角边之和为8,两直角边分别为多少时,此三角形的面积最大?最大值是多少?
课堂练习
5.如图,有长为30 m的篱笆,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x m,面积为y m2.
(1)求y与x的函数解析式;
(2)y是否有最大值?如果有,请求出y的最大值.
解:(1)若AB=x m,则BC=(30-3x)m,
x
30-3x
∴y=-3x2+30x.
(2)y=-3x2+30x=-3(x-5)2 +75
当x=5时,函数y有最大值为75.
x能取“5”吗?
课堂练习
5.如图,有长为30 m的篱笆,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x m,面积为y m2.
(1)求y与x的函数解析式;
(2)y是否有最大值?如果有,请求出y的最大值.
x
30-3x
解:(2)y=-3x2+30x=-3(x-5)2+75
∵3x<30且30-3x≤10,
∴
∵在对称轴x=5的右侧,y随x的增大而减小,
∴当x= 时,y最大值为
课堂小结
二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
22.3第1课时
二次函数与图形面积问题
人教版 九年级上册
教学目标
教学目标:
1.能够从实际问题中抽象出二次函数关系.(重点)
2.会运用二次函数知识求实际问题中的最大值或最小值,解决实际问题.(难点)
3.能应用二次函数的性质解决图形中的最大面积问题.
新知导入
思考 排球运动员从地面竖直向上抛出排球,排球的高度 h(单位:m)与排球的运动时间 t(单位:s)之间的关系式是h= 20t - 5t 2 (0≤t≤4).排球的运动时间是多少时,排球最高?排球运动中的最大高度是多少?
0
h
t
4
新知讲解
问题 从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 h=30t-5t2(0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
可以出,这个函数的图象是一条抛物看线的一部分,这条抛物线的顶点是这个函数的图象的最高点.也就是说,当t取顶点的横坐标时,这个函数有最大值.
新知讲解
小球运动的时间是 3s 时,小球最高.小球运动中的最大高度是 45 m.
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
解:由题意得:
【想一想】如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
总结归纳
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值 .
新知讲解
探究1 用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
分析 先写出 S 关于 l 的函数解析式,再求出使 S 最大 的l 值.
解: 矩形场地周长为 60 m ,一边长为 l m,所以另一边长为 m,
场地的面积 S =l(30-l)
即 S=-l2+30l (0
S有最大值.
方法总结
二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
课堂练习
1.用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形菜园的最大面积是________.
A. 6厘米 B. 12厘米 C. 24厘米 D. 36厘米
2.某种正方形合金板材的成本y(元)与它的面积成正比,设边长为厘米,当x=3时,y=18那么当成本为78元时,边长为( )
A
课堂练习
3.用长12 m的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是( )
A.9 m2 B.2 m2 C.6 m2 D.8 m2
C
课堂练习
解:设一直角边长为x,则另一直角边长为 ,依题意得:
4.已知直角三角形的两直角边之和为8,两直角边分别为多少时,此三角形的面积最大?最大值是多少?
课堂练习
5.如图,有长为30 m的篱笆,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x m,面积为y m2.
(1)求y与x的函数解析式;
(2)y是否有最大值?如果有,请求出y的最大值.
解:(1)若AB=x m,则BC=(30-3x)m,
x
30-3x
∴y=-3x2+30x.
(2)y=-3x2+30x=-3(x-5)2 +75
当x=5时,函数y有最大值为75.
x能取“5”吗?
课堂练习
5.如图,有长为30 m的篱笆,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x m,面积为y m2.
(1)求y与x的函数解析式;
(2)y是否有最大值?如果有,请求出y的最大值.
x
30-3x
解:(2)y=-3x2+30x=-3(x-5)2+75
∵3x<30且30-3x≤10,
∴
∵在对称轴x=5的右侧,y随x的增大而减小,
∴当x= 时,y最大值为
课堂小结
二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
